Тема 4. Непрерывные функции
одной переменной
4.1. Непрерывность функции в точке и на
промежутке
4.2.
Точки разрыва функции и их классификация
4.1.
Непрерывность функции в точке и на промежутке
Определение 1. Функция f(x)
называется непрерывной в точке x0ÎD(f), если она определена в некоторой
окрестности точки x0 и предел f(x) в точке x0
равен
значению функции в этой точке, т.е.
![]() .
.
Замечание. Из определения 1 следует правило вычисления предела
функции в точке её непрерывности:
![]()
т.е. предел функции в точке её
непрерывности равен значению функции в этой точке.
Определение 2. Функция f(x)
называется непрерывной в точке x0ÎD(f), если она
определена в некоторой окрестности этой точки и бесконечно малому приращению
аргумента ![]() соответствует
бесконечно малое приращение функции
соответствует
бесконечно малое приращение функции ![]() , т.е.
, т.е. ![]() .
.
Определение 3. Функция f(x) называется
непрерывной в точке x0ÎD(f), если она
определена в некоторой окрестности этой точки и существует правый и левый
предел f(x) в точке![]() , причём они равны
между собой и равны значению функции
в этой точке, т.е.
, причём они равны
между собой и равны значению функции
в этой точке, т.е.
![]() ;
; ![]() ;
; ![]() .
.
Определение 4. Функция f(x)
называется непрерывной на промежутке, если она непрерывна в каждой точке этого
промежутка.
Теоремы о непрерывных
функциях
Теорема 8. Если функции f(x) и g(x) непрерывны в точке x0 , то функции с×f(x) (c=const),
f(x) ± g(x),
f(x)×g(x) и ![]() (если g(x) ¹ 0) также непрерывны в точке x0.
(если g(x) ¹ 0) также непрерывны в точке x0.
Теорема 9. Если функция u = u(x) непрерывна
в точке x0 и функция y = f(u) непрерывна в точке u0 = u(x0), то сложная функция y = f(u(x))
непрерывна в точке x0.
Теорема 10. Все элементарные функции непрерывны
в каждой точке области их определения.
4.2.
Точки разрыва функции и их классификация
Определение 5. Точка x0 называется точкой разрыва функции f(x), если в
этой точке функция либо не определена, либо определена, но нарушено хотя бы
одно из условий определения 3 непрерывности f(x).
Определение 6. Точка x0 называется точкой устранимого разрыва функции f(x), если предел функции в этой точке существует, но f(x) в точке x0 либо не определена, либо имеет
значение f(x0), не совпадающее с найденным
пределом:
f(x0 – 0) = f(x0 + 0) ¹ f(x0).
Определение 7.
Точка x0 называется точкой разрыва первого рода функции f(x) (разрыв типа «скачка»), если в этой точке функция
имеет конечные, но не равные между собой правый и левый пределы, т.е.
f(x0 – 0) ¹ f(x0 + 0).
Определение 8.
Точка x0 называется точкой разрыва второго рода функции f(x), если в этой точке функция не имеет хотя бы одного
из односторонних пределов или хотя бы один из односторонних пределов
бесконечен.
Примеры.
Исследовать функции на непрерывность и точки разрыва.
1. 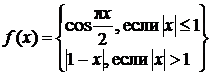
Решение. На
промежутке (–∞; –1) ![]() , на промежутке (–1;1)
, на промежутке (–1;1)
![]() и на промежутке (1;+∞)
и на промежутке (1;+∞) ![]() .
.
На этих промежутках элементарная
функция f(x) непрерывна
при всех x, принадлежащих этим промежуткам.
Необходимо проверить непрерывность в точках x = –1 и x = 1.
1)
![]()
2)
![]()
Получили, что f(–1–0) ¹ f(–1+0) => x = –1 –
точка разрыва функции f(x) I рода.
3)
![]()
4) ![]()
Получили, что f(1 – 0) = f(1 + 0) = f(1) = 0 => x = 1 – точка
непрерывности функции f(x).
Ответ: f(x) непрерывна на промежутках (–∞;–1)
и на (–1;+∞), точка x = –1 – точка разрыва функции f(x) I рода.
2. f(x) = ![]()
Решение. На
промежутках (–∞;0) и на (0;+∞) функция f(x) непрерывна. Исследуем точку x = 0 Ï D(f).
1) ![]()
2)
![]() x = 0 –
точка разрыва функции f(x) II рода.
x = 0 –
точка разрыва функции f(x) II рода.