Тема 3. Предел функции одной
переменной
3.1. Предел функции в конечной точке
3.3. Предел функции на бесконечности
3.4. Бесконечно малые и бесконечно большие
функции
3.5. Основные теоремы о конечных пределах
3.6. Первый замечательный предел
3.7. Второй замечательный предел
3.1. Предел функции в
конечной точке
Определение 1. Окрестностью
точки x0 называется любой интервал, содержащий
точку x0:
.
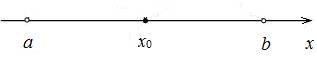
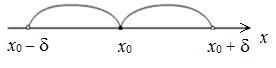
Определение 2. d-Окрестностью
точки x0 называется интервал (
; 
), длина которого 2d, симметричный относительно x0:
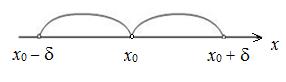
Определение 3. Проколотой d-окрестностью
точки x0 называется d-окрестность точки x0 без самой точки x0:
Определение 4. Число А называется пределом функции f(x) при
x ® x0, если для любого малого числа ε
> 0 существует такое малое число 
, что для любого x, принадлежащего
D(f) и проколотой
δ-окрестности точки x0, т.е. 
, выполняется неравенство: 
.
Итак: 
и 
.
3.2. Односторонние пределы
Определение 5. Число А называется правым (левым)
пределом функции y = f(x) в
точке x0, если для любого малого числа ε > 0 найдётся
другое малое число – такое, что для всех 
и лежащих в правой
(левой) окрестности точки x0, т.е. 
, справедливо неравенство: 
При этом используют следующие
обозначения:
– для правого предела.
– для левого предела.
Замечание 1.
Если f(x) имеет в точке x0, предел равный А,
то существуют
и 
и справедливо
равенство: 
.
Замечание 2. Если f(x) имеет
в точке x0 правый 
и левый 
пределы, равные между
собой, то в точке 
функция f(x) имеет предел, равный числу: 
.
Замечание 3. Если f(x) имеет
в точке x0 правый 
и левый 
пределы, но они не
равны между собой, то в точке x0 функция f(x) не имеет
предела.
3.3. Предел функции на
бесконечности
Определение 6. Окрестностью бесконечно удалённой точки называют множество значений x, удовлетворяющих неравенству 
, где N достаточно
большое положительное число.
Определение 7. Число А называется пределом функции f(x) при 
, если для любого малого числа ε > 0 существует
другое большое число 
– такое, что для
любого 
удовлетворяющего
неравенству 
выполняется неравенство 
. Этот факт
записывают: 
.
3.4. Бесконечно малые и бесконечно большие функции
Определение 8. Функция a(x) называется бесконечно
малой при x ® x0 или в точке 
, если предел a(x) при
x®
равен нулю: 
.
Определение 9. Функция f(x) называется бесконечно большой в точке 
, если предел f(x) при x ® x0 равен ∞. Это значит, что для
любого сколь угодно большого числа M > 0 существует малое число δ = δ(M) > 0 такое, что для любого удовлетворяющего
неравенству , выполняется неравенство |f(x)| > M.
Определение 10. Функция f(x) называется ограниченной на некотором множестве X Ì D(f), если существует такое число M > 0, что для любого x Î X выполняется неравенство |f(x)| < M.
Основные свойства бесконечно малых функций
1) Алгебраическая сумма конечного числа бесконечно малых функций в
точке 
есть бесконечно
малая функция в этой точке , т.е. если 
– бесконечно малые
функции в точке , то 
– бесконечно малая
функция в этой точке .
2) Произведение конечного числа бесконечно малых функций в точке есть бесконечно малая функция в точке , т.е. если – бесконечно малые
функции в точке , то 
– бесконечно малая
функция в этой точке .
3) Произведение бесконечно малой
функции в точке на ограниченную
функцию в некоторой окрестности точки есть бесконечно
малая функция в точке, т. е.
если α(x) бесконечно малая функция в точке и f(x)
ограниченная в некоторой окрестности точки , то α(x)×f(x) – бесконечно малая функция в точке.
Следствие из свойства 3). Произведение постоянной c на бесконечно малую функцию α(x) в точке есть бесконечно малая функция в точке, т.е. если
α(x) – бесконечно малая
функция в точке , то с×α(x) – бесконечно малая функция в точке x0.
Теорема (о связи между бесконечно
малой функцией в точке x0 и бесконечно большой функцией в
точке x0)
Если функция f(x) является бесконечно большой в точке , то функция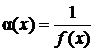 
является бесконечно
малой в точке . (Верно и
обратное утверждение)
3.5. Основные теоремы о
конечных пределах
Теорема 1. Функция f(x) имеет конечный предел в точке 
тогда и только тогда, когда выполняется равенство: f(x) = А+a(x), где a(x) – бесконечно малая функция в точке .
Доказательство этой теоремы вытекает
из определения предела функции в точке и определения бесконечно малой функции в
точке.
Теорема 2. Если
существуют конечные пределы двух функций f(x) и g(x) в точке , то
существует конечный предел суммы этих функций в точке , равный сумме пределов этих функций.
Доказательство:
Пусть 
, тогда по теореме 1 f(x) = А+a(x), где a(x) –
бесконечно малая функция в точке x0. Пусть 
, тогда по теореме 1g(x) = B + β(x), где β(x) –
бесконечно малая функция в точке x0. Рассмотрим сумму этих функций:
f(x) + g(x) = A + a(x) + B + β(x) = (A+B) + a(x) + β(x).
Обозначим γ(x) = a(x) + β(x) – бесконечно малая функция в точке x0 (по свойству 1 бесконечно малых
функций). Получим f(x) + g(x)=A + B + γ(x).
По теореме 1: 
.
Теорема доказана.
Теорема 3. Если
существуют конечные пределы двух функций f(x) и g(x) в точке , то
существует предел произведения этих
функций в точке, равный произведению
пределов этих функций.
Доказательство: Пусть, тогда по теореме 1: f(x) = А+a(x), где a(x) – бесконечно малая функция в точке . Пусть 
, тогда по теореме 1: g(x) = B + β(x), где β(x) – бесконечно малая функция в точке . Рассмотрим
произведение этих функций:
f(x) × g(x) = (А +a(x))(B + β(x)) = A×B + B×a(x) + A×β(x) + a(x) ×β(x).
Обозначим: B×a(x) + A×β(x) + a(x) ×β(x) = γ(x), где γ(x) –
бесконечно малая функция в точке (по свойствам бесконечно малых функций).
Получим: f(x)×g(x) = A×B + γ(x).
По теореме 1: 
.
Теорема доказана.
Теорема 4. Если существуют конечные пределы f(x)
и g(x), причём 
, то существует предел частного этих функций 
в точке , равный
частному пределов этих функций, т. е.: если существует и существует
, B ≠ 0,
то существует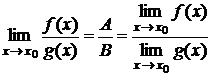 
(доказать
самостоятельно).
Теорема 5 (о пределе трёх функций). Если существуют равные конечные
пределы функций f(x) и g(x) в точке:
и при стремлении x к x0 выполняется неравенство: 
φ(x) 
то существует 
φ(x), равный А.
Доказательство:
Возьмем любое e > 0. Вычитая из всех частей двойного неравенства,
данного в условии, число A, получим
φ(x) 
(1)
Так как
, то найдётся такое d1, что для всех x ¹ x0, удовлетворяющих условию 
, будет верно
неравенство , или, что то же,
. (1)
Аналогично для функции g(x) найдётся такое d2, что для всех x ¹ x0, удовлетворяющих условию 
, будет верно неравенство 
. (1)
Из неравенств, отмеченных (1), следует, что 
φ(x)
,
или, что то же самое |φ(x)
для всех x ¹ x0, удовлетворяющих
условию 
, где d
– меньшее из d1 и d2. Это означает, что 
φ(x).
Теорема доказана.
3.6. Первый замечательный
предел
Теорема. Предел
функции 
в точке 
существует и
равен 1, т.е.
.
Доказательство:
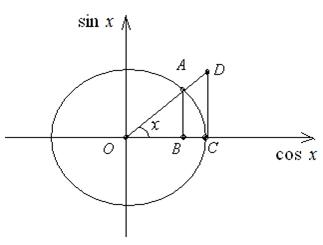
1) Пусть угол x
> 0 (x 
). Площади
соотносятся:
(1)
; 
; 
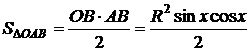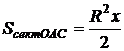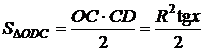, где угол х в
радианах.
Подставим
в соотношение (1) полученные значения площадей:
, 
, 
.
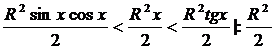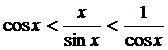Так как все части двойного неравенства
положительные, выражение можно переписать так: 
.
Так как 
то по теореме 5: 
.
2) Пусть x < 0 (x 
)
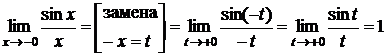(по доказанному в первом случае). Следовательно, 
.
Теорема доказана.
3.7. Второй замечательный
предел
Теорема. Предел
функции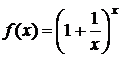 
при x
существует и равен числу e, т.е.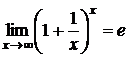 
.
Замечание. Число e является пределом последовательности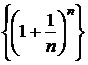
, причем это число иррациональное, т.е. представляется
бесконечной непериодической десятичной
дробью: e = 2,7182818284590… . Более того, число
e трансцендентное, т.е. не является
корнем алгебраического уравнения с целыми коэффициентами. В математическом
анализе это число играет особую роль, в частности, является основанием
натурального логарифма. Показательная функция с основанием e: 
, называется экспонентой.
Модификация второго замечательного
предела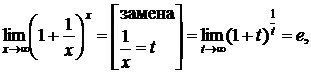 
т.е.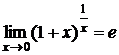 
.