МИНИСТЕРСТВО
ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное
государственное бюджетное образовательное учреждение высшего профессионального
образования
«Дагестанский
государственный университет»
Факультет математики
и компьютерных наук
Кафедра математического анализа
Курс лекций
по дисциплине
МАТЕМАТИЧЕСКИЙ АНАЛИЗ
(I семестр)
Направление 10.03.01 - Информационная безопасность
Профиль подготовки Безопасность компьютерных систем
Степень
выпускника: бакалавр
Форма
обучения: очная
Автор-составитель
Магомедова Вазипат Гусеновна
Махачкала 2017
Модуль 1. Начала анализа
Тема 1. Множества.
Логические символы. Отображение и функция. Графики
Тема 2. Действительные
числа и их последовательности
Модуль
2. Производная функции одной переменной
Тема 5. Производная и
дифференциал функции одной переменной
Тема 6. Теоремы о
среднем дифференциального исчисления
Тема 7. Производные
высших порядков. Формула Тейлора
Тема 8. Исследование
поведения функции с помощью производных
Модуль 3. Функции многих переменных
Тема 9. Понятие сходимости в конечномерном пространстве
Тема 10. Пределы и непрерывность функции многих переменных
Тема 11. Частные производные и дифференциалы. Формула Тейлора
Тема 12. Задачи на экстремум функции многих переменных
Литература
Модуль 1
Тема
1. Множества. Логические символы. Отображение и функция. Графики
1. Множества. Операции над
множествами
В математике первичными
понятиями являются понятия множества
и элемента множества. Множества
обозначают большими латинскими буквами A, B, ..., а их элементы – малыми a, b, ... Если элемент a принадлежит множеству A, то пишут aÎA. В противном случае пишут aÏA.
Множество, не содержащее
ни одного элемента, называется пустым
и обозначается Æ.
Множество A называется подмножеством множества B, если любой элемент множества A является элементом множества B. Пишут AÌB или BÉA и говорят, что множество A включено во
множество B или B включает A.
Множества A и B называются равными, если они состоят из одних и тех же элементов. Записывают
это так: A=B.
Включение AÌB не исключает равенства этих множеств.
Если же AÌB, но A¹B и A¹Æ, то A называют собственным подмножеством множества B.
Если множество A включено во множество B или совпадает с ним, то пишут AÍB или BÊA.
Множество называется конечным, если оно содержит конечное
число элементов. Множество, не являющееся конечным, называется бесконечным.
 Если заданы два множества A и B, то через AÈB обозначается множество, называемое их объединением или суммой и
состоящее из всех тех элементов, каждый из которых принадлежит хотя бы одному
из множеств A и B. Таким
образом, если некоторый элемент принадлежит множеству AÈB, то он принадлежит либо только множеству A, либо только множеству B, либо обоим
этим множествам одновременно.
Если заданы два множества A и B, то через AÈB обозначается множество, называемое их объединением или суммой и
состоящее из всех тех элементов, каждый из которых принадлежит хотя бы одному
из множеств A и B. Таким
образом, если некоторый элемент принадлежит множеству AÈB, то он принадлежит либо только множеству A, либо только множеству B, либо обоим
этим множествам одновременно.
Для любого множества A (непустого или пустого) полагается AÈÆ=A.
Через A∩B обозначается множество, состоящее из
всех элементов, которые одновременно принадлежат как множеству A, так и множеству B. Множество A∩B называется пересечением множеств A и B. Если A и B не имеют общих элементов (в
частности, одно из них или оба пусты), то полагают A∩B=Æ. В этом случае множества A и B называются непересекающимися.
 Отметим, что пустое множество
совпадает само с собой: Æ=Æ, но вместе с тем оно не пересекается
само с собой: Æ∩Æ=Æ.
Отметим, что пустое множество
совпадает само с собой: Æ=Æ, но вместе с тем оно не пересекается
само с собой: Æ∩Æ=Æ.
Через ![]() обозначается множество, называемое разностью множеств A и B и состоящее из всех элементов,
которые принадлежат множеству A, но не принадлежат множеству B. Говорят также, что
обозначается множество, называемое разностью множеств A и B и состоящее из всех элементов,
которые принадлежат множеству A, но не принадлежат множеству B. Говорят также, что ![]() получается из
множества A вычитанием из
него множества B.
получается из
множества A вычитанием из
него множества B.
Если BÌA, то разность ![]() называется дополнением множества B до множества A. По
определению, полагается
называется дополнением множества B до множества A. По
определению, полагается ![]() .
.
Логические символы
В математических
рассуждениях часто встречаются выражения «существует элемент», обладающий некоторыми
свойствами, и «любой элемент» среди элементов, имеющих некоторое свойство.
Вместо слова «существует» или равносильного ему слова «найдётся» иногда пишут
символ $, т. е. перевернутую латинскую букву E (от англ. Existence существование), а вместо слов
«любой», «каждый», «всякий» – символ ", т. е. перевернутое латинское A (от англ. аny любой). Символ $
называется символом существования, а
символ " – символом всеобщности.
Кроме того, в
математических доказательствах часто используют символ Þ,
который означает «следует» (одно высказывание следует из другого), и символ Û,
который означает равносильность высказываний, стоящих по разные от него
стороны.
2.
Понятие функции
Пусть даны два
множества ![]() и
и ![]() . Если каждому элементу
. Если каждому элементу ![]() по некоторому закону
или правилу соответствует определенный элемент
по некоторому закону
или правилу соответствует определенный элемент ![]() , то это соответствие называется однозначной функцией
или отображением множества
, то это соответствие называется однозначной функцией
или отображением множества ![]() в
множество
в
множество ![]() . Множество
. Множество ![]() называется областью
определения или существования этой функции. Функция обозначается
называется областью
определения или существования этой функции. Функция обозначается ![]() ,
, ![]() или
или ![]() . Переменная
. Переменная ![]() называется независимой
переменной или аргументом функции, а переменная
называется независимой
переменной или аргументом функции, а переменная ![]() называется зависимой
переменной или функцией.
называется зависимой
переменной или функцией.
Если элемент ![]() соответствует элементу
соответствует элементу
![]() при отображении
при отображении ![]() , то
, то ![]() называется образом
называется образом
![]() , а
, а ![]() – прообразом
– прообразом
![]() .
.
Множество всех
образов при отображении ![]() называется множеством
значений этой функции или областью изменения функции.
называется множеством
значений этой функции или областью изменения функции.
Способы задания
функции
1) Аналитический способ - указывается
формула, которая служит законом соответствия и связывает зависимую и
независимую переменные: ![]() . Например,
. Например, ![]() .
.
2) Табличный способ
задания функции – например, таблицы Брадиса
задают функции y = sin x, y = cos x и др.
3) Графический способ задания функции, когда зависимость функции от её
аргумента задаётся графически.
3.
Сложная и обратная функции
Определение 1. Пусть
функция y = f(U) определена на множестве D(f), а функция U = g(x) определена на D(g), причём E(g)![]() D(f).
D(f).
Тогда функция y = F(x) = f(g(x)) называется сложной
функцией (или функцией от функции, или суперпозицией
функций f и
g ).
Определение 2. Пусть задана
функция y = f(x) взаимно однозначно
отображающая множество X = D(f) на множество Y = E(f).
Тогда функция x = g(y) называется обратной
к функции y =
f(x), т. е.
любому y![]() E(f) соответствует
единственное значение x
E(f) соответствует
единственное значение x![]() D(f), при
котором верно равенство y =
f(x).
D(f), при
котором верно равенство y =
f(x).
Замечание.
Графики функций y = f(x) и x = g(y) представляют
одну и ту же кривую. Если же у обратной функции независимую переменную
обозначить x, а зависимую y, то графики функций y = f(x) и y = g(x) будут
симметричны относительно биссектрисы первого и третьего координатных углов.
4. Элементарные функции
Основные элементарные функции:
y =
const (постоянная
функция), D(y) = R; E(y) = c.
![]() (линейная функция), D(y) = R; E(y) = R.
(линейная функция), D(y) = R; E(y) = R.
y =![]() (степенная функция), α ÎR, E(y), D(y) зависят от
α.
(степенная функция), α ÎR, E(y), D(y) зависят от
α.
y =
![]() (показательная функция), a >
(показательная функция), a >
y =![]() (логарифмическая функция) ), a >
(логарифмическая функция) ), a >
Тригонометрические функции:
y =
sin x, D(y) = R, E(y) =![]() .
.
y = cos x, D(y)
= R, E(y) =![]() .
.
y = tg x, D(y)
= ![]() , E(y) = R.
, E(y) = R.
y = ctg x, D(y)
= ![]() , E(y) = R.
, E(y) = R.
Обратные тригонометрические функции:
y =
arcsin x, D(y) = ![]() , E(y) =
, E(y) = ![]() .
.
y = arccos x, D(y)
= ![]() , E(y) =
, E(y) = ![]() .
.
y = arctg x, D(y)
= R, E(y) = ![]() .
.
y = arcctg x, D(y)
= R, E(y) = ![]() .
.
Элементарной функцией называется функция, составленная из основных элементарных функций с помощью
конечного числа операций сложения, вычитания, умножения, деления и
суперпозиции.
Например: ![]() – элементарная функция.
– элементарная функция.
Графики обратных тригонометрических функций:
|
y = arcsin x
|
y = arccos
x
|
|
y = arctg x
|
y = arcctg x
|
Тема
2. Действительные числа и их
последовательности
Множеством
натуральных чисел называются числа, используемые при счете и обозначается ![]() . Множество всех натуральных чисел, ноль и числа,
противоположные натуральным, образуют множество целых чисел:
. Множество всех натуральных чисел, ноль и числа,
противоположные натуральным, образуют множество целых чисел: ![]() .
.
Рациональным
числом называют число, представимое в виде отношения некоторого целого
числа к некоторому натуральному числу. Множество всех рациональных чисел
обозначается через ![]() . Следовательно,
. Следовательно,

Хотя
рациональных чисел бесконечно много, их не хватает для измерения длин,
площадей, объемов и т.д.
Измерить
длину отрезка означает сравнить его с другим отрезком. Оказывается, если взять два
произвольных отрезка с длинами ![]() и
и ![]() , то не всегда с помощью одного можно найти длину другого,
если ограничиться только множеством рациональных чисел. Таковыми являются,
например, сторона и диагональ квадрата. Если взять в качестве масштабной
единицы какой-нибудь отрезок, сторону и диагональ нельзя выразить с помощью рациональных
чисел. Следовательно, для измерения величин (длины, площади т.д.) нужно
расширить множество рациональных чисел.
, то не всегда с помощью одного можно найти длину другого,
если ограничиться только множеством рациональных чисел. Таковыми являются,
например, сторона и диагональ квадрата. Если взять в качестве масштабной
единицы какой-нибудь отрезок, сторону и диагональ нельзя выразить с помощью рациональных
чисел. Следовательно, для измерения величин (длины, площади т.д.) нужно
расширить множество рациональных чисел.
Заметим,
что любое рациональное число можно представить в виде некоторой бесконечной
периодической десятичной дроби. Для этого достаточно числитель разделить на
знаменатель в столбик.
Аналогично
каждую бесконечную десятичную дробь можно обратить в обыкновенную дробь.
Поэтому рациональное число можно определить следующим образом: рациональным
числом называется бесконечная периодическая десятичная дробь, взятая со
знаком «+» или «-».
Легко
привести примеры десятичных дробей, которые не являются периодическими. Таковой
является, например, дробь 0,1010010001… Число 1 не является периодом, так как как угодно далеко в записи этой
дроби встречаются нули. Аналогично ноль не является периодом. Следовательно,
существуют непериодические десятичные дроби, они называются иррациональными
числами. Множество иррациональных чисел обозначается ![]() Оказывается,
если объединить все периодические и непериодические десятичные дроби, то задача
измерения величин полностью решается.
Оказывается,
если объединить все периодические и непериодические десятичные дроби, то задача
измерения величин полностью решается.
Множество
всех рациональных и иррациональных чисел образует множество действительных чисел.
Обозначается ![]() .
.
Последовательность.
Предел последовательности
Пусть X – какое-либо множество и ¥ – множество натуральных чисел. Если каждому элементу множества ¥ поставлен в соответствие единственный
вполне определённый элемент множества X, то говорят, что задана последовательность.
Соответствующий натуральному числу n элемент множества X обозначается через xn и называется n-м членом последовательности. Сама эта последовательность обозначается через {xn} или xn, n = 1, 2, ...
Постоянное число a называется пределом последовательности xn, если для любого e>0 существует такой номер N(e), что все значения xn, у которых номер n>N, удовлетворяют неравенству ![]() .
.
Если выполняется это условие, то пишут ![]() или xn®a при n®¥ и говорят, что члены
последовательности {xn} стремятся к a. Сама последовательность в этом случае называется сходящейся.
или xn®a при n®¥ и говорят, что члены
последовательности {xn} стремятся к a. Сама последовательность в этом случае называется сходящейся.
Бесконечно малые и бесконечно большие
последовательности
Последовательность, имеющая своим пределом нуль, называется бесконечно малой.
Если в определении предела последовательности положить a=0, то неравенство ![]() примет вид
примет вид ![]() .
.
Таким образом, данное выше определение бесконечно малой можно
подробнее сформулировать без упоминания термина «предел»: последовательность
называется бесконечно малой, если она
по абсолютной величине становится и остаётся меньшей сколь угодно малого
наперёд заданного числа e > 0, начиная с некоторого номера.
Можно показать, что, если последовательность xn®a, то она может быть представлена в виде ![]() , где an есть бесконечно малая, и обратно, если последовательность xn допускает такое определение, то она имеет пределом a. Это следует из того, что
, где an есть бесконечно малая, и обратно, если последовательность xn допускает такое определение, то она имеет пределом a. Это следует из того, что ![]() .
.
Этим свойством часто пользуются на практике для установления
предела последовательности.
Последовательность xn называется бесконечно большой,
если она по абсолютной величине становится и остаётся большей сколь угодно
большого наперёд заданного числа Е >
0, начиная с некоторого номера: ![]() .
.
Примеры. Бесконечно большими являются
следующие последовательности: ![]() .
.
Если последовательность xn является бесконечно большой и, начиная с некоторого
n, сохраняет определённый знак (+ или-), то в соответствии со знаком
говорят, что последовательность xn имеет предел +¥ или –¥, и пишут:
![]() .
.
Очевидно, что бесконечно большая величина xn в общем случае характеризуется соотношением: |xn|®+¥.
Теорема 1. Любая сходящаяся последовательность
имеет единственный предел.
Теорема 2. Если для двух последовательностей xn, yn всегда выполняется неравенство xn ³ yn, причём каждая из них имеет конечный предел: xn ® a, yn ® b, то a ³ b.
Теорема 3. Если для последовательностей xn, yn, zn всегда выполняются неравенства xn£yn£zn, причём ![]() , тогда
, тогда ![]() .
.
Свойства
бесконечно малых последовательностей
1. Сумма любого конечного числа бесконечно малых величин есть также
величина бесконечно малая.
2. Произведение ограниченной последовательности xn на бесконечно малую an величину есть бесконечно малая
величина.
Теорема 4. Если последовательности xn, yn имеют конечные пределы: ![]() , то и сумма (разность) их также
имеет конечный предел, причём
, то и сумма (разность) их также
имеет конечный предел, причём ![]() .
.
Теорема 5. Если последовательности xn, yn имеют конечные пределы: ![]() , то их произведение также имеет
конечный предел, причём
, то их произведение также имеет
конечный предел, причём ![]() .
.
Теорема 6. Если последовательности xn, yn имеют конечные пределы: ![]() , b ¹ 0, то их отношение также имеет конечный предел, причём
, b ¹ 0, то их отношение также имеет конечный предел, причём  .
.
Предел монотонной ограниченной
последовательности
Последовательность xn называется возрастающей (неубывающей),
если ![]() .
.
Последовательность xn называется убывающей (невозрастающей),
если ![]() .
.
В первом случае говорят, что последовательность «монотонно возрастает», во втором – что
она «монотонно убывает». В целом
последовательности такого вида называют монотонными.
Теорема 7 (теорема Вейерштрасса). Пусть дана монотонно возрастающая последовательность xn. Если она ограничена сверху: ![]() , то имеет конечный предел, в
противном случае – стремится к +¥.
, то имеет конечный предел, в
противном случае – стремится к +¥.
Точно так же, всегда имеет предел и монотонно убывающая
последовательность xn. Её предел конечен, если она ограничена снизу: ![]() , в противном же случае её пределом
служит –¥.
, в противном же случае её пределом
служит –¥.
Критерий
сходимости Коши
Назовём последовательность фундаментальной (сходящейся в
себе, последовательностью Коши),
если для каждого числа e > 0 существует такой номер N,
что неравенство ![]() выполняется для всех n1>N, n2>N.
выполняется для всех n1>N, n2>N.
Теорема (критерий
сходимости Коши). Для того чтобы последовательность
xn имела конечный предел, необходимо и
достаточно, чтобы она была фундаментальной.
Тема
3. Теория
пределов
1.
Предел функции в конечной точке x0
Определение 1. Окрестностью
точки x0 называется любой интервал, содержащий
точку x0:

![]() .
.
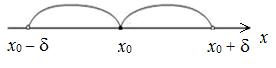
Определение 2. d-Окрестностью
точки x0 называется интервал
(![]() ;
; ![]() ), длина которого 2d, симметричный относительно x0:
), длина которого 2d, симметричный относительно x0:
![]()
Определение 3. Проколотой d-окрестностью точки x0 называется d-окрестность точки x0 без самой точки x0:
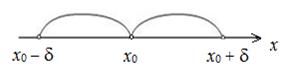
![]()
Определение 4. Число А называется пределом функции f(x)
при x ® x0, если для любого малого числа ε > 0
существует такое малое число ![]() , что для любого x, принадлежащего
D(f) и проколотой
δ-окрестности точки x0, т.е.
, что для любого x, принадлежащего
D(f) и проколотой
δ-окрестности точки x0, т.е. ![]() , выполняется неравенство:
, выполняется неравенство: ![]() .
.
Итак: ![]() и
и ![]() .
.
2.
Односторонние пределы
Определение 5. Число А называется правым (левым) пределом функции
y = f(x) в точке x0, если для любого малого числа ε > 0 найдётся
другое малое число ![]() – такое, что для всех
– такое, что для всех ![]() и лежащих в правой
(левой) окрестности точки x0, т.е.
и лежащих в правой
(левой) окрестности точки x0, т.е. ![]() , справедливо неравенство:
, справедливо неравенство: ![]() .
.
При этом используют следующие
обозначения:
![]() – для правого предела.
– для правого предела.
![]() – для левого предела.
– для левого предела.
Замечание 1.
Если f(x) имеет в точке x0, предел равный А, то существуют![]() и
и ![]() и справедливо
равенство:
и справедливо
равенство: ![]() .
.
Замечание 2. Если f(x)
имеет в точке x0 правый ![]() и левый
и левый ![]() пределы, равные между
собой, то в точке
пределы, равные между
собой, то в точке ![]() функция f(x) имеет предел, равный числу:
функция f(x) имеет предел, равный числу: ![]() .
.
Замечание 3. Если f(x)
имеет в точке x0 правый ![]() и левый
и левый ![]() пределы, но они не
равны между собой, то в точке x0 функция f(x) не имеет
предела.
пределы, но они не
равны между собой, то в точке x0 функция f(x) не имеет
предела.
3.
Предел функции на бесконечности
Определение 6. Окрестностью бесконечно удалённой точки называют множество значений x, удовлетворяющих неравенству ![]() , где N достаточно
большое положительное число.
, где N достаточно
большое положительное число.
Определение 7. Число А называется пределом функции f(x) при ![]() , если для любого малого числа ε > 0 существует
другое большое число
, если для любого малого числа ε > 0 существует
другое большое число ![]() – такое, что для
любого
– такое, что для
любого ![]() удовлетворяющего
неравенству
удовлетворяющего
неравенству ![]() выполняется неравенство
выполняется неравенство ![]() . Этот факт записывают:
. Этот факт записывают:
![]() .
.
4.
Бесконечно малые и бесконечно большие функции
Определение 8. Функция a(x) называется бесконечно
малой при x ® x0 или в точке ![]() , если предел a(x) при
x®
, если предел a(x) при
x®![]() равен нулю:
равен нулю: ![]() .
.
Определение 9. Функция f(x) называется бесконечно большой в точке ![]() , если предел f(x)
при x ® x0 равен ∞. Это значит, что для
любого сколь угодно большого числа M > 0 существует малое число δ = δ(M) > 0 такое, что для любого
, если предел f(x)
при x ® x0 равен ∞. Это значит, что для
любого сколь угодно большого числа M > 0 существует малое число δ = δ(M) > 0 такое, что для любого ![]() удовлетворяющего
неравенству
удовлетворяющего
неравенству ![]() , выполняется неравенство |f(x)| > M.
, выполняется неравенство |f(x)| > M.
Определение 10. Функция f(x) называется ограниченной на некотором множестве X Ì D(f), если существует такое число M > 0, что для любого x Î X
выполняется неравенство |f(x)| < M.
Основные свойства бесконечно малых функций
1) Алгебраическая сумма конечного числа бесконечно малых функций в
точке ![]() есть бесконечно
малая функция в этой точке
есть бесконечно
малая функция в этой точке ![]() , т.е. если
, т.е. если ![]() – бесконечно малые
функции в точке
– бесконечно малые
функции в точке ![]() , то
, то ![]() – бесконечно малая
функция в этой точке
– бесконечно малая
функция в этой точке ![]() .
.
2) Произведение конечного числа бесконечно малых функций в точке ![]() есть бесконечно малая функция в точке
есть бесконечно малая функция в точке ![]() , т.е. если
, т.е. если ![]() – бесконечно малые
функции в точке
– бесконечно малые
функции в точке ![]() , то
, то ![]() – бесконечно малая
функция в этой точке
– бесконечно малая
функция в этой точке ![]() .
.
3) Произведение бесконечно малой
функции в точке ![]() на ограниченную
функцию в некоторой окрестности точки
на ограниченную
функцию в некоторой окрестности точки ![]() есть бесконечно
малая функция в точке
есть бесконечно
малая функция в точке![]() , т. е.
если α(x) бесконечно малая функция в точке
, т. е.
если α(x) бесконечно малая функция в точке ![]() и f(x) ограниченная в
некоторой окрестности точки
и f(x) ограниченная в
некоторой окрестности точки ![]() , то α(x)×f(x) –
бесконечно малая функция в точке
, то α(x)×f(x) –
бесконечно малая функция в точке![]() .
.
Следствие из свойства 3). Произведение постоянной c на бесконечно малую функцию α(x) в точке ![]() есть бесконечно малая функция в точке
есть бесконечно малая функция в точке![]() , т.е. если
α(x) – бесконечно малая
функция в точке
, т.е. если
α(x) – бесконечно малая
функция в точке ![]() , то с×α(x) – бесконечно малая функция в точке x0.
, то с×α(x) – бесконечно малая функция в точке x0.
Теорема (о связи между бесконечно
малой функцией в точке x0 и бесконечно большой функцией в
точке x0)
Если функция f(x) является бесконечно большой в точке ![]() , то функция
, то функция  является бесконечно
малой в точке
является бесконечно
малой в точке ![]() . (Верно и
обратное утверждение)
. (Верно и
обратное утверждение)
5.
Основные теоремы о конечных пределах
Теорема 1. Функция f(x) имеет конечный предел в точке ![]() тогда и только тогда, когда выполняется равенство: f(x) = А+a(x), где a(x) – бесконечно малая функция в точке
тогда и только тогда, когда выполняется равенство: f(x) = А+a(x), где a(x) – бесконечно малая функция в точке ![]() .
.
Доказательство этой теоремы вытекает
из определения предела функции в точке и определения бесконечно малой функции в
точке.
Теорема 2. Если
существуют конечные пределы двух функций f(x) и g(x) в точке ![]() , то
существует конечный предел суммы этих функций в точке
, то
существует конечный предел суммы этих функций в точке ![]() , равный сумме пределов этих функций.
, равный сумме пределов этих функций.
Доказательство:
Пусть ![]() , тогда по теореме 1 f(x) = А+a(x), где a(x) –
бесконечно малая функция в точке x0. Пусть
, тогда по теореме 1 f(x) = А+a(x), где a(x) –
бесконечно малая функция в точке x0. Пусть ![]() , тогда по теореме 1g(x) = B +
β(x), где β(x) – бесконечно малая функция в точке x0. Рассмотрим сумму этих функций:
, тогда по теореме 1g(x) = B +
β(x), где β(x) – бесконечно малая функция в точке x0. Рассмотрим сумму этих функций:
f(x) + g(x) = A + a(x) + B + β(x) = (A+B) + a(x) + β(x).
Обозначим γ(x) = a(x) + β(x) – бесконечно малая функция в точке x0 (по свойству 1 бесконечно малых
функций). Получим f(x) + g(x)=A + B + γ(x).
По теореме 1: ![]() .
.
Теорема доказана.
Теорема 3. Если
существуют конечные пределы двух функций f(x) и g(x) в точке ![]() , то
существует предел произведения этих
функций в точке
, то
существует предел произведения этих
функций в точке![]() , равный
произведению пределов этих функций.
, равный
произведению пределов этих функций.
Доказательство: Пусть![]() , тогда по теореме 1: f(x) = А+a(x), где a(x) – бесконечно малая функция в точке
, тогда по теореме 1: f(x) = А+a(x), где a(x) – бесконечно малая функция в точке ![]() . Пусть
. Пусть ![]() , тогда по теореме 1: g(x) = B + β(x), где β(x) –
бесконечно малая функция в точке
, тогда по теореме 1: g(x) = B + β(x), где β(x) –
бесконечно малая функция в точке ![]() . Рассмотрим
произведение этих функций:
. Рассмотрим
произведение этих функций:
f(x) × g(x) = (А +a(x))(B + β(x)) = A×B + B×a(x) + A×β(x) + a(x) ×β(x).
Обозначим: B×a(x) + A×β(x) + a(x) ×β(x) = γ(x), где γ(x) –
бесконечно малая функция в точке ![]() (по свойствам бесконечно малых функций).
Получим: f(x)×g(x) = A×B + γ(x).
(по свойствам бесконечно малых функций).
Получим: f(x)×g(x) = A×B + γ(x).
По теореме 1: ![]() .
.
Теорема доказана.
Теорема 4. Если существуют конечные пределы f(x) и g(x), причём ![]() , то существует предел частного этих функций
, то существует предел частного этих функций ![]() в точке
в точке ![]() , равный
частному пределов этих функций, т. е.: если существует
, равный
частному пределов этих функций, т. е.: если существует ![]() и существует
и существует
![]() , B ≠ 0, то
существует
, B ≠ 0, то
существует
 (доказать
самостоятельно).
(доказать
самостоятельно).
Теорема 5 (о пределе трёх функций). Если существуют равные конечные
пределы функций f(x) и g(x) в точке![]() :
: ![]() и при стремлении x к x0 выполняется неравенство:
и при стремлении x к x0 выполняется неравенство: ![]() φ(x)
φ(x) ![]() , то существует
, то существует ![]() φ(x), равный А.
φ(x), равный А.
6.
Первый замечательный предел
Теорема 6. Предел
функции ![]() в точке
в точке ![]() существует и
равен 1, т.е.
существует и
равен 1, т.е.![]() .
.
Доказательство:
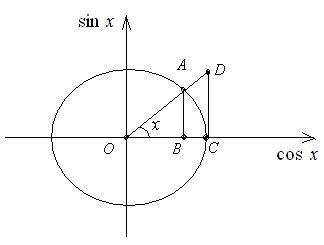
1)
Пусть угол x > 0 (x ![]() ). Площади
). Площади![]() соотносятся:
соотносятся: ![]() . Имеем
. Имеем  ;
;  ;
;  , где угол х
в радианах.
, где угол х
в радианах.
Подставим
в соотношение (1) полученные значения площадей:
 ,
, ![]() ,
,  .
.
Так как все части двойного неравенства
положительные, выражение можно переписать так:
![]() . Так как
. Так как ![]() то по теореме 5:
то по теореме 5: ![]() .
.
2) Пусть x < 0 (x
![]() ). Тогда
). Тогда  (по доказанному в первом случае).
Следовательно,
(по доказанному в первом случае).
Следовательно, ![]() .
.
Теорема доказана.
7.
Второй замечательный предел
Теорема 7. Предел
функции  при x
при x![]() существует и равен числу e, т.е.
существует и равен числу e, т.е.  .
.
Замечание. Число e является пределом последовательности , причем это число иррациональное, т.е. представляется
бесконечной непериодической десятичной
дробью: e = 2,7182818284590… . Более того,
число e трансцендентное, т.е. не является
корнем алгебраического уравнения с целыми коэффициентами. В математическом
анализе это число играет особую роль, в частности, является основанием
натурального логарифма. Показательная функция с основанием e:
, причем это число иррациональное, т.е. представляется
бесконечной непериодической десятичной
дробью: e = 2,7182818284590… . Более того,
число e трансцендентное, т.е. не является
корнем алгебраического уравнения с целыми коэффициентами. В математическом
анализе это число играет особую роль, в частности, является основанием
натурального логарифма. Показательная функция с основанием e: ![]() , называется экспонентой.
, называется экспонентой.
Модификация второго замечательного
предела  т.е.
т.е.  .
.
Тема
4. Непрерывные
функции
1.
Непрерывность функции в точке и на промежутке
Определение 1. Функция f(x) называется непрерывной в точке x0ÎD(f), если она определена в некоторой
окрестности точки x0 и предел f(x) в точке x0
равен
значению функции в этой точке, т.е. ![]() .
.
Замечание. Из определения 1 следует правило вычисления предела
функции в точке её непрерывности: ![]()
т.е. предел функции в точке её
непрерывности равен значению функции в этой точке.
Определение 2. Функция f(x) называется
непрерывной в точке x0ÎD(f), если она определена
в некоторой окрестности этой точки и бесконечно малому приращению аргумента ![]() соответствует
бесконечно малое приращение функции
соответствует
бесконечно малое приращение функции ![]() , т.е.
, т.е. ![]() .
.
Определение 3. Функция f(x) называется непрерывной в
точке x0ÎD(f), если она
определена в некоторой окрестности этой точки и существует правый и левый
предел f(x) в точке![]() , причём они равны
между собой и равны значению функции
в этой точке, т.е.
, причём они равны
между собой и равны значению функции
в этой точке, т.е.
а) ![]() ;
;
б) ![]() ;
;
в) ![]() .
.
Определение 4. Функция f(x) называется
непрерывной на промежутке, если она непрерывна в каждой точке этого промежутка.
Теоремы о непрерывных
функциях
Теорема 8. Если функции f(x) и g(x) непрерывны в точке x0 , то функции с×f(x) (c=const),
f(x) ± g(x),
f(x)×g(x) и ![]() (если g(x) ¹ 0) также непрерывны в точке x0.
(если g(x) ¹ 0) также непрерывны в точке x0.
Теорема 9. Если функция u = u(x) непрерывна в точке x0 и функция y = f(u) непрерывна
в точке u0 = u(x0), то сложная функция y = f(u(x)) непрерывна в точке x0.
Теорема 10. Все элементарные функции непрерывны
в каждой точке области их определения.
2.
Точки разрыва функции и их классификация
Определение 5. Точка x0 называется точкой разрыва функции f(x), если в
этой точке функция либо не определена, либо определена, но нарушено хотя бы
одно из условий определения 3 непрерывности f(x).
Определение 6. Точка x0 называется точкой устранимого разрыва функции f(x), если предел функции в этой точке существует, но f(x) в точке x0 либо не определена, либо имеет
значение f(x0), не совпадающее с найденным
пределом: f(x0 – 0) = f(x0 + 0) ¹ f(x0).
Определение 7.
Точка x0 называется точкой разрыва первого рода функции f(x) (разрыв типа «скачка»), если в этой точке функция
имеет конечные, но не равные между собой правый и левый пределы, т.е. f(x0 – 0) ¹ f(x0 + 0).
Определение 8.
Точка x0 называется точкой разрыва второго рода функции f(x), если в этой точке функция не имеет хотя бы одного
из односторонних пределов или хотя бы один из односторонних пределов
бесконечен.
Примеры.
Исследовать функции на непрерывность и точки разрыва.
1. 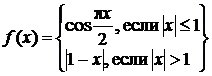
Решение. На
промежутке (–∞; –1) ![]() , на промежутке (–1;1)
, на промежутке (–1;1)
![]() и на промежутке (1;+∞)
и на промежутке (1;+∞) ![]() .
.
На этих промежутках элементарная
функция f(x) непрерывна
при всех x, принадлежащих этим промежуткам.
Необходимо проверить непрерывность в точках x = –1 и x = 1.
1)
![]()
2) ![]()
Получили, что f(–1–0) ¹ f(–1+0) => x = –1 – точка разрыва функции f(x) I рода.
3) ![]()
4) ![]()
Получили, что f(1 – 0) = f(1 + 0) = f(1) = 0 => x = 1 – точка непрерывности функции f(x).
Ответ: f(x) непрерывна на промежутках (–∞;–1)
и на (–1;+∞), точка x =
–1 – точка разрыва функции f(x) I рода.
2. f(x) = ![]()
Решение. На
промежутках (–∞;0) и на (0;+∞) функция f(x) непрерывна. Исследуем точку x = 0 Ï D(f).
1)
![]()
2) ![]() x = 0 – точка разрыва функции f(x) II рода.
x = 0 – точка разрыва функции f(x) II рода.
Модуль 2
Тема
5. Производная и дифференциал функции
одной переменной
1.
Определение производной, её геометрический и механический
смысл
Пусть дана функция ![]() , определённая на множестве D(f). Рассмотрим точку xÎD(f) и некоторое число Dx – такое,
чтобы точка x+DxÎD(f). Это число Dx называется приращением аргумента x.
, определённая на множестве D(f). Рассмотрим точку xÎD(f) и некоторое число Dx – такое,
чтобы точка x+DxÎD(f). Это число Dx называется приращением аргумента x.
Определение 1.
Приращением функции ![]() называется
разность f(x+Dx) – f(x). Приращение функции
называется
разность f(x+Dx) – f(x). Приращение функции ![]() обозначают Dy, т.е. Dy = f(x+Dx) – f(x).
обозначают Dy, т.е. Dy = f(x+Dx) – f(x).
Определение 2. Производной
функции ![]() называется предел
отношения приращения функции Dy к приращению аргумента Dx, если приращение аргумента Dx стремится к нулю и этот предел
существует. Производную функции
называется предел
отношения приращения функции Dy к приращению аргумента Dx, если приращение аргумента Dx стремится к нулю и этот предел
существует. Производную функции ![]() обозначают:
обозначают: ![]() или
или ![]() . Поэтому можно записать:
. Поэтому можно записать:
![]()
Пример. Исходя из определения найти производную функции у =![]() .
.
Решение.
Dy= f(x+ Dx) – f(x) =  .
.
 .
.
Ответ:  .
.![]()
Механический смысл производной
Пусть материальная точка движется по прямой по закону S =
S(t),
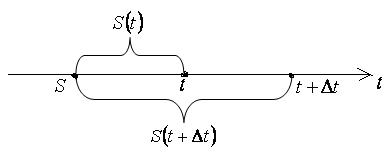
тогда DS = S(t+Dt) – S(t) –
расстояние, пройденное за время Dt и средняя
скорость движения: ![]() .
.
Чтобы найти скорость движения в
момент времени t, надо рассмотреть предел ![]() при Dt ® 0:
V(t) =
при Dt ® 0:
V(t) = ![]() .
.
Следовательно, производная от пути S(t) равна мгновенной скорости точки в
момент времени t :
![]() .
.
Геометрический смысл производной
Рассмотрим график функции y = f(x) в окрестности фиксированной точки М0 (рис. 5).
Точка M0(x0;y(x0)) – фиксированная точка графика ![]() . Точка M(x0+Dx; y(x0+Dx)) при
различных значениях Dx – любая точка на графике. Если точка M приближается к точке M0 (при этом Dx ® 0), то
секущая линия M0M стремится к
своему предельному положению, называемому касательной
к линии y = f(x) в точке M0.
. Точка M(x0+Dx; y(x0+Dx)) при
различных значениях Dx – любая точка на графике. Если точка M приближается к точке M0 (при этом Dx ® 0), то
секущая линия M0M стремится к
своему предельному положению, называемому касательной
к линии y = f(x) в точке M0.
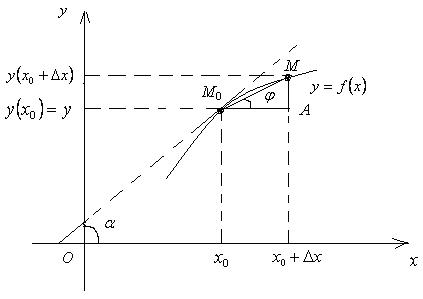
Рис. 5
Рассмотрим
треугольник M0MA: tg j =  , j –
угол наклона секущей M0 M к оси Ox.
, j –
угол наклона секущей M0 M к оси Ox.
Перейдем к пределу при Dx ®0:
 j =
j = ![]() , где
, где![]() – угол наклона касательной к оси Ox.
– угол наклона касательной к оси Ox.
Таким образом, y' (x0) = tg![]() частное значение производной функции
частное значение производной функции ![]() в точке x0 равно угловому коэффициенту касательной, проведённой
к линии y =
f(x) в точке M0(x0; y(x0)). Тогда, используя уравнение прямой, проходящей
через заданную точку M0(x0;y0) с известным угловым коэффициентом Kкас = y'(x0), можно записать уравнение касательной к линии y =
f(x) в точке M0(x0; f(x0)): y = f(x0) + f ' (x0) × (x – x0).
в точке x0 равно угловому коэффициенту касательной, проведённой
к линии y =
f(x) в точке M0(x0; y(x0)). Тогда, используя уравнение прямой, проходящей
через заданную точку M0(x0;y0) с известным угловым коэффициентом Kкас = y'(x0), можно записать уравнение касательной к линии y =
f(x) в точке M0(x0; f(x0)): y = f(x0) + f ' (x0) × (x – x0).
Аналогично, можно записать уравнение нормали – прямой, перпендикулярной
касательной и проходящей через точку касания M0(x0;f(x0)):
y =
f(x0) – ,
,
используя условие перпендикулярности прямых: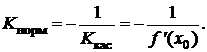
2.
Примеры вывода производных некоторых элементарных функций
1) ![]()
Вывод: ![]() ;
; ![]()
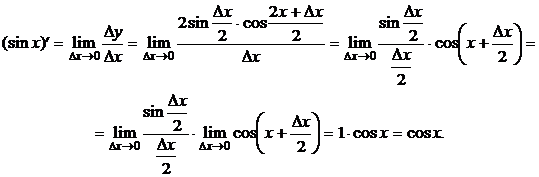
2) ![]() .
Вывод:
.
Вывод: ![]() ;
; ![]()
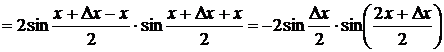

3) ![]() . Вывод:
. Вывод: ![]() ;
; 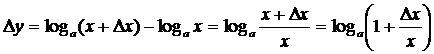
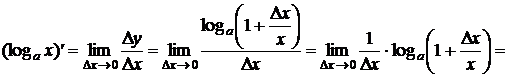
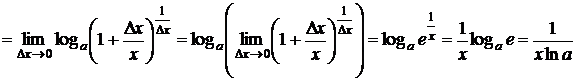
(используется второй замечательный предел и свойства
логарифма).
4) ![]() . Вывод: так как ln x = log e x, то,
используя производную, для (log a x), можно записать:
. Вывод: так как ln x = log e x, то,
используя производную, для (log a x), можно записать:
 .
.
5) (c)' = 0. Вывод: y = c, Dy = y(x+Dx) – y(x) = c – c = 0 ![]() .
.
Для остальных функций производные выводятся позже с помощью
правил дифференцирования.
3.
Таблица производных основных элементарных функций
1.
(c)' = 0
2.
(xa)' = a×xa –
1
3.
(ax)'
= ax×ln a, (a >
4.
(ex)' = ex
5.
(loga x)' =  , (a > 0; a ≠ 1)
, (a > 0; a ≠ 1)
6.
(ln x)' = ![]()
7.
(sin x)' =cos x
8.
(cos x)' = – sin x
9.
(tg x)' = ![]()
10.
(ctg x)' = – ![]()
11.
(arcsin x)' = ![]()
12.
(arccos x)' = –![]()
13.
(arctg x)' = 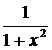
14.
(arcctg x)' = ![]()
4.
Дифференцируемость функции. Связь дифференцируемости с существованием
производной и непрерывностью функции
Определение 3. Функция y = f(x) называется
дифференцируемой в точке xÎD(f), если она определена в некоторой
окрестности точки x и её приращение в этой точке можно представить в виде:
Dx = A×Dx + ![]() (Dx)×Dx,
(Dx)×Dx,
где A = A(x) – не
зависит от Dx; ![]() (Dx) – бесконечно малая величина при Dx®0, т.е.
(Dx) – бесконечно малая величина при Dx®0, т.е. ![]()
Теорема 1 (связь дифференцируемости с
существованием производной)
Функция y = f(x) дифференцируема в точке xÎD(f) тогда и только тогда, когда она
имеет в этой точке производную f '(x). При этом f '(x) = A.
Доказательство.
1) Необходимость: Дано: y =
f(x) дифференцируема в точке х. Доказать: A = f '(x). Так как функция y = f(x)
дифференцируема в точке х,
то по определению Dy = A × Dx + ![]() (Dx) × Dx, где
(Dx) × Dx, где ![]() (Dx) ® 0 при Dx ® 0.
(Dx) ® 0 при Dx ® 0.
Разделим это равенство на Dx ≠ 0: ![]()
![]() . Перейдём к пределу при Dx ® 0:
. Перейдём к пределу при Dx ® 0: ![]() существует, а значит f '(x) = A.
существует, а значит f '(x) = A.
Необходимость доказана.
2) Достаточность:
Дано: f ' (x) –
существует. Доказать: f(x) дифференцируема.
Так как существует f '(x)=![]() , то по свойству предела можно записать:
, то по свойству предела можно записать: ![]() , где
, где ![]() (Dx) ® 0 при D x® 0. Умножим это равенство на Dx:
(Dx) ® 0 при D x® 0. Умножим это равенство на Dx: ![]() Þ функция y = f(x), дифференцируема
в точке х.
Þ функция y = f(x), дифференцируема
в точке х.
Достаточность доказана.
Теорема 2 (связь дифференцируемости с
непрерывностью функции)
Если функция y = f(x) дифференцируема в точке xÎD(f), то она непрерывна в этой точке.
Доказательство. Так как функция дифференцируема в точке x, то её приращение в этой точке можно представить в
виде: Dy = A × Dx +
![]() (Dx) × Dx, где A =
f '(x) и
(Dx) × Dx, где A =
f '(x) и ![]() (Dx) ® 0 при Dx ® 0.
(Dx) ® 0 при Dx ® 0.
Найдём предел от Dy при Dx ® 0:
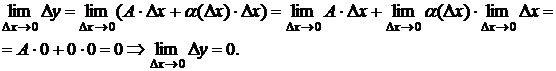
Отсюда следует, что по определению 2
непрерывности функции в точке функция y = f(x) непрерывна
в точке x.
Замечание.
Обратное теореме 2 утверждение не всегда верно.
5.
Правила дифференцирования
Теорема 3. Если функции
U(x) и V(x) дифференцируемы в точке x, то функция U(x) ± V(x) дифференцируема в точке x и её
производная вычисляется по формуле:
(U(x)
± V(x))'
= (U(x))'
± (V(x))'.
Доказательство: Рассмотрим функцию y = U(x) ± V(x).
Тогда Dy = DU ± DV. Разделим на Dx и перейдём к пределу при Dx ® 0:  так как по условию
теоремы функции U(x) и V(x) дифференцируемы.
так как по условию
теоремы функции U(x) и V(x) дифференцируемы.
Значит, (U(x) ± V(x))' = U '(x) ± V '(x).
Теорема доказана.
Теорема 4. Если функции U(x) и V(x) дифференцируемы в точке х, то функция (U(x)×V(x)) дифференцируема в точке х и её
производная вычисляется по формуле: (U(x) × V(x))' = (U(x))'× V(x) + U(x) × (V(x))'.
Доказательство.
Рассмотрим функцию ![]() . Найдём её приращение
. Найдём её приращение
Dy =
(U+DU)(V+DV)
– U×V = U×V + U×DV + V×DU + DU×DV – U×V=
= U×DV + V×DU + DU×DV.
Разделим Dy на Dx и перейдем
к пределу при Dx ® 0:

![]()
так как по условию функции U(x) и V(x) дифференцируемы, а значит ![]() ,
,  и
и ![]() .
.
Следовательно, (U(x)× V(x))' = U ' (x) × V(x) + U(x) × V ' (x).
Теорема доказана.
Следствия:
а) Если U(x), V(x) и W(x) дифференцируемы
в точке х,
то функция (U(x)×V(x) ×W(x)) дифференцируема в точке х и её
производная вычисляется по формуле:
(U×V×W)' = U '×V×W + U×V '×W + U×V×W '.
б)
Производная постоянной,
умноженной на дифференцируемую функцию, равна этой постоянной, умноженной на
производную функции: (C×U(x))' = C×U ' (x).
Теорема 5. Если функции U(x) и V(x) дифференцируемы в точке х и V(x) ≠ 0,
то функция ![]() дифференцируема в
точке х и
её производная вычисляется по формуле:
дифференцируема в
точке х и
её производная вычисляется по формуле:  .
.
Доказательство.
Рассмотрим функцию  . Найдём её приращение
. Найдём её приращение
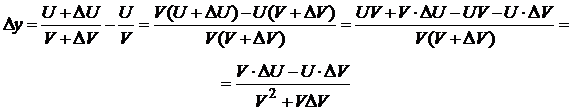
Разделим Dy на Dx и перейдём к пределу при Dx ® 0:  ,
,
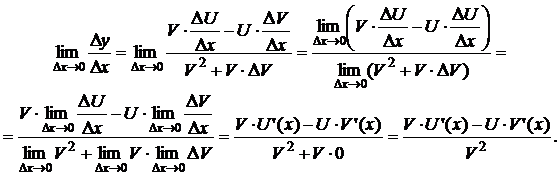
Значит,  .
.
Теорема доказана.
Теорема 6 (производная сложной
функции). Если
функция f(u)
дифференцируема в точке u, а функция u(x) дифференцируема в точке x, причём u =
u(x), тогда
сложная функция f(u(x)) дифференцируема в точке x и её производная вычисляется по
формуле: (f (u(x)))' = f '(u) ×u' (x).
Доказательство.
Рассмотрим функцию y =
f(u). Так как
функция f(u)
дифференцируема в точке u, то её приращение можно записать в
виде: ![]() , где
, где ![]() .
.
Разделим на Dx и перейдём
к пределу при Dx ® 0: ![]()

Если D x® 0, то D u® 0, так как u(x) дифференцируема, а значит непрерывна, т.е.
(f(u(x)))' = f ' (u) ×u' (x).
Теорема доказана.
Теорема 9. Если функции U(x) и V(x) дифференцируемы в точке x, то
показательно-степенная функция y = (U(x))V(x)
дифференцируема в точке x и справедлива формула:
![]() .
.
Доказательство можно выполнить с
помощью логарифмирования равенства y = (U(x))V(x)
по основанию логарифма e и дальнейшего дифференцирования
обеих частей полученного равенства.
6.
Производные обратных тригонометрических функций
Теорема 10. Функция y = arcsin x дифференцируема при любом xÎ(–1;1) и справедлива формула: 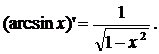
Доказательство:
Функция y =
arcsin x определена
при x Î[–1;1] и область ее значений  . Она монотонно возрастает на всей области её определения,
поэтому имеет обратную функцию x =
sin y. Уравнение x = sin y можно рассматривать как неявное задание функции y = arcsin x. Найдём производную от обеих частей уравнения:
. Она монотонно возрастает на всей области её определения,
поэтому имеет обратную функцию x =
sin y. Уравнение x = sin y можно рассматривать как неявное задание функции y = arcsin x. Найдём производную от обеих частей уравнения: ![]() .
.
Выразим из полученного равенства y':  .
.
Но ![]() при
при  . Поэтому
. Поэтому ![]() , так как
, так как ![]() . Следовательно, получаем:
. Следовательно, получаем:  .
.
Аналогично,
функция y =
arсcos x дифференцируема при x Î(–1;1) и справедлива формула:  .
.
Функция
y =
arctg x
дифференцируема при x Î(–¥;+¥) и справедлива формула:  .
.
Функция
y =
arcсtg x дифференцируема при x Î(–¥;+¥) и справедлива формула:  .
.
7.
Дифференциал функции
Пусть функция y = f(x) дифференцируема в точке x, тогда её
приращение можно записать в виде двух слагаемых, первое из которых линейно
относительно Dx, а второе
слагаемое – бесконечно малая величина при
Dx ® 0 (более высокого порядка малости по
сравнению с Dx): ![]() , где
, где ![]() (Dx) ® 0 при Dx ® 0.
(Dx) ® 0 при Dx ® 0.
Определение 4. Слагаемое ![]() называется главной линейной относительно Dx частью приращения функции y =
f(x),
называемой дифференциалом этой
функции. Дифференциал обозначается dy = y' (x)× Dx .
называется главной линейной относительно Dx частью приращения функции y =
f(x),
называемой дифференциалом этой
функции. Дифференциал обозначается dy = y' (x)× Dx .
Если x –
независимая переменная, то справедливо равенство Dx = dx, так как (x)' = 1. Тогда формула для дифференциала записывается: dy =
y' (x)× dx .
Так как второе слагаемое приращения
функция – малая величина более высокого порядка малости по сравнению с Dx, то между приращением функции и её дифференциалом можно приближённо поставить знак
равенства. Это равенство тем точнее, чем меньше Dx. На основе этого приближённого равенства получается
приближённое представление значения дифференцируемой функции:
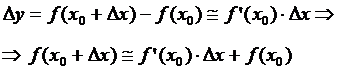
Геометрический смысл дифференциала
Рассмотрим график дифференцируемой функции y = f(x) в некоторой окрестности точки x0 (рис. 6):
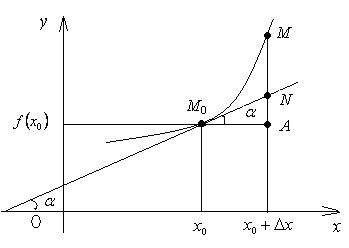
Рис. 6
Из DM0AN
AN = M0A×tg a =
Dx×f '(x0) = dy.
Итак: дифференциал функции y =
f(x) в точке x0 равен
приращению ординаты касательной (AN), проведённой к кривой y = f(x) в точке (x0; f(x0)), при переходе от x0 к x0+Dx (от точки М0 в точку М).
Инвариантность формы дифференциала
Теорема 14. Пусть функция
y =
f(u)
дифференцируема в точке u, а функция u = u(x)
дифференцируема в соответствующей точке x (u =
u(x)). Тогда
для сложной функции y =
f(u(x)) справедливо равенство: dy = f '(u)du = y'(x)dx.
Доказательство.
Сложная функция y=f(u(x)) является дифференцируемой в точке x. Поэтому справедливо равенство: dy = y'(x)dx .
Но так как функция y(x) = f(u(x)) сложная,
то y' (x) = f ' (u) × u' (x). Поэтому dy = y'(x)dx =
f '(u)×u'(x)dx = f '(u)×du, так как по условию теоремы функция u = u(x)
дифференцируема в точке x, следовательно, du = u' (x)×dx.
Теорема доказана.
8.
Производные и дифференциалы высших порядков
Если функция y = f(x) дифференцируема на некотором промежутке, то она
имеет на этом
промежутке производную y' = f ' (x), которая
в свою очередь может иметь
производную: (y')' = (f '(x))' = y'', называемую второй производной функции y = f(x). Она
обозначается:  .
.
Может случиться, что новая функция y''(x) имеет производную, тогда она
называется третьей производной
функции y = f(x) и
обозначается:  .
.
Производная “n”-го порядка
функции y =
f(x)
обозначается:  .
.
Дифференциалом второго порядка функции y = f(x) в точке x называется
выражение, обозначаемое d2y и вычисляемое по формуле: ![]() , если x – независимая переменная.
, если x – независимая переменная.
Дифференциал третьего порядка функции y = f(x): ![]() ,
,
если x – независимая переменная, и т.д.
Замечание. Дифференциал уже второго порядка не
обладает свойством инвариантности формы.
Тема 6. Теремы о среднем
дифференциального исчисления
Теорема 1. Если функция f(x) непрерывна на отрезке [a;b], то она достигает на этом отрезке
своих наименьшего m и наибольшего M значений, т.е. для любых
x Î [a;b]
выполняется неравенство: m ≤ f(x)
≤ M.
Теорема 2. Если функция f(x) непрерывна на отрезке [a;b], то для любого числа С,
удовлетворяющего неравенству m ≤ С ≤ M, на отрезке [a;b] найдётся хотя бы одна точка х0, в которой выполняется равенство: f(х0)
= С.
Теорема 3. Если функция f(x) непрерывна на отрезке [a;b] и на концах этого отрезка имеет
значения различных знаков, то существует хотя бы одна точка х0
Î (a;b), в которой выполняется равенство: f(х0)
= 0.
1.
Теорема Ролля
Теорема 4 (теорема Ролля). Если функция f(x) определена на отрезке [a;b] и выполнены следующие условия:
· f(x) непрерывна на отрезке [a;b];
· f(x) дифференцируема на интервале (a;b);
· f(a) = f(b),
то внутри этого отрезка [a;b] найдется хотя бы одна точка х0,
в которой выполняется равенство: f '(х0) = 0.
Доказательство. Так как f(x) непрерывна
на отрезке [a;b], то она
достигает на этом отрезке своих наименьшего m и
наибольшего M значений.
Возможны два случая: m = M и m < M.
· Если m = M, то f(x) = const = m = M. Тогда f '(x) = 0 при любом x Î
[a;b].
Следовательно, в этом случае теорема верна и при этом в качестве х0 можно
рассматривать любое значение x Î
[a;b].
· Если m < M, то исходя из условия f(a) = f(b), по
крайней мере одно из чисел m или M не равно f(a) = f(b). Для определённости предположим,
что M – наибольшее значение f(x) достигается не на концах отрезка [a;b], а в некоторой внутренней точке х0
Î (a;b). Тогда в точке х0 для приращения функции справедливо
неравенство: Dy = f(х0 +
Dx) – f(хо)
≤ 0, так как f(х0)
= M – наибольшее значение f(x) на
отрезке [a;b] и Dx такое, что х0
+ D x Î
[a;b].
· Если D x > 0, то ![]() и существует
и существует ![]()
·
Если
D x < 0, то ![]() и существует
и существует ![]()
Так как по условию теоремы функция f(x) дифференцируема при xÎ
(a;b), то в
точке хо существует производная. Значит справедливы
равенства: f ' (х0 + 0) = f ' (х0
– 0) = f ' (х0) = 0.
Теорема доказана.
Геометрический смысл теоремы Ролля
С геометрической точки зрения теорема
Ролля означает, что график функции, непрерывной на
отрезке [a;b],
дифференцируемой на интервале (a;b) и
принимающей на концах отрезка равные значения, имеет хотя бы одну точку с
координатами (х0 ; f (х0)),
где х0Î (a;b), в которой касательная параллельна оси Ox (рис. 7).
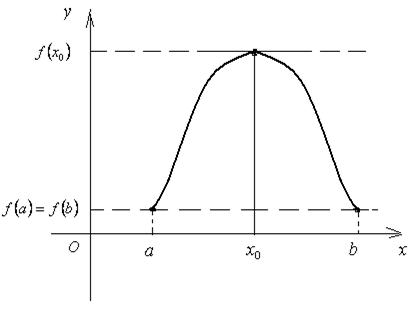
Рис.
7
2.
Теорема Лагранжа
Теорема 5 (теорема Лагранжа). Если функция f(x) определена на отрезке [a;b] и выполнены следующие условия:
· f(x) непрерывна на отрезке [a;b],
· f(x) дифференцируема на интервале (a;b),
то внутри этого отрезка существует
хотя бы одна точка х0, в которой выполняется равенство: f ' (х0) = ![]() .
.
Доказательство. Рассмотрим вспомогательную функцию F(x) =
f(x) + l×x, где l = const. Потребуем, что бы для F(x) выполнялось условие F(a) = F(b).
Так как F(a) = f(a) + l×a и F(b) = f(b) + l×b, то получим равенство: f(a) + l×a =
f(b) + l×b.
Отсюда выразим значение l:
l = – ![]() . При этом значении l
функция F(x) = f(x) –
. При этом значении l
функция F(x) = f(x) – ![]() .
.
Функция F(x)
удовлетворяет всем условиям теоремы Ролля:
· F(x) непрерывна на отрезке [a;b]:
· F(x) дифференцируема на интервале (a;b)
· F(a) = F(b).
Следовательно, по теореме Ролля на
интервале (a;b) существует
хотя бы одна точка х0, в которой выполняется равенство: F '(х0) = 0.
Найдём F '(x): F '(x) = f '(x) –  .
Поэтому F '(x0) = f '(х0) –
.
Поэтому F '(x0) = f '(х0) –![]() = 0, если f '(х0)
=
= 0, если f '(х0)
= ![]() .
.
Теорема доказана.
Геометрический смысл теоремы Лагранжа
С геометрической точки зрения теорема
Лагранжа означает, что график функции, непрерывной на отрезке [a;b] и дифференцируемой на интервале (a;b), имеет хотя бы одну точку (х0; f(х0),
в которой касательная параллельна секущей, проходящей через точки A(a; f(a)) и B(b; f(b)) (рис. 8)
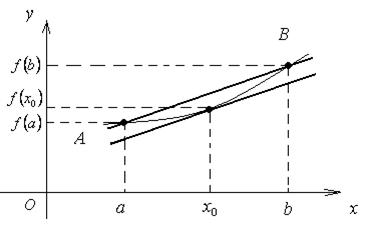
Рис. 8
3.
Теорема Коши
Теорема 6 (теорема Коши). Если функции f(x) и g(x) определены на отрезке [a;b] и удовлетворяют условиям:
· f(x)
и g(x) непрерывны
на отрезке [a;b];
· f(x) и g(x) дифференцируемы на интервале (a;b);
· g '(x) ¹ 0 при любом x Î (a;b),
то внутри отрезка [a;b] найдётся хотя бы одна точка х0,
в которой выполняется равенство:  .
.
Доказательство аналогично доказательству теоремы 5 (теорема Лагранжа)
при вспомогательной функции F(x) = f(x) + l × g(x),
где l = const, которую выбирают так, чтобы F(a) = F(b).
4.
Правило Лопиталя
Теорема 7 (правило Лопиталя). Если функции f(x) и g(x) определены в некоторой окрестности
точки х0
и в этой окрестности они удовлетворяют условиям:
· f(x) и g(x)
дифференцируемы в каждой точке за исключением может быть самой точки х0;
· g '(x) ¹ 0 для любого x из этой окрестности;
·
![]() или
или ![]() ,
,
тогда, если существует конечный или бесконечный, то
выполняется равенство:
конечный или бесконечный, то
выполняется равенство:  =
=  .
.
Замечание 1. Правило Лопиталя
используется для раскрытия неопределённостей типа ![]() или
или ![]() , возникающих при вычислении пределов. Если под знаком
предела оказывается неопределённость другого типа: 0×∞,
, возникающих при вычислении пределов. Если под знаком
предела оказывается неопределённость другого типа: 0×∞,
![]() , 10, 00 или ∞0, то с
помощью тождественных алгебраических преобразований такая неопределённость
приводится к
, 10, 00 или ∞0, то с
помощью тождественных алгебраических преобразований такая неопределённость
приводится к ![]() или
или ![]() и тогда можно
применить правило Лопиталя.
и тогда можно
применить правило Лопиталя.
Замечание 2. Если к условиям теоремы 7 добавить дифференцируемость
функций f '(x) и g'(x) в окрестности точки х0,
то при выполнении остальных требований для f '(x) и g'(x) правило Лопиталя можно
применить повторно. При этом будет справедливо равенство:  =
=  =
= 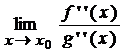
Пример 1. Вычислить предел: 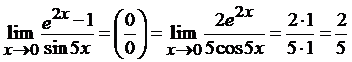
Пример 2.
Вычислить предел: 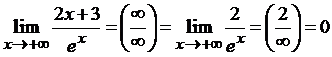
Тема
7. Производные высших порядков. Формула Тейлора
1.
Определение производных высших порядков
Пусть функция ![]() , определённая на интервале
, определённая на интервале ![]() , имеет в каждой точке
, имеет в каждой точке ![]() производную
производную ![]() и пусть
и пусть ![]() . Если при x = x0 у производной
. Если при x = x0 у производной ![]() функции
функции ![]() существует
производная, то она называется второй
производной (или производной второго
порядка) функции f и обозначается
существует
производная, то она называется второй
производной (или производной второго
порядка) функции f и обозначается ![]() или
или ![]() .
.
Таким образом, ![]() . Аналогично определяется производная
. Аналогично определяется производная ![]() любого порядка n=1, 2, ...: если существует производная
любого порядка n=1, 2, ...: если существует производная ![]() порядка n–1 (при этом под производной нулевого порядка подразумевается сама
функция
порядка n–1 (при этом под производной нулевого порядка подразумевается сама
функция ![]() , а под производной первого порядка –
, а под производной первого порядка – ![]() ), то, по определению,
), то, по определению, ![]() .
.
Вспоминая определение производной, определение n-й производной в точке x0 можно записать в виде предела:
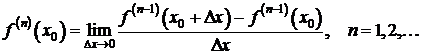
Отметим, из предположения, что функция f имеет в точке x0 производную порядка n, отсюда следует, в силу определения
последней, что в некоторой окрестности точки x0 у функции f существует производная порядка n–1, а, следовательно, при n > 1 и все производные более
низкого порядка k < n–1, в частности, сама функция определена в некоторой окрестности точки x0. При этом все производные, порядок
которых меньше n–1, непрерывны в указанной окрестности, поскольку во всех её точках они
имеют производную.
Функция называется n раз непрерывно дифференцируемой на некотором
промежутке, если во всех точках этого промежутка она имеет непрерывные
производные до порядка n включительно (n = 1, 2, ...).
Для того чтобы функция была n раз непрерывно дифференцируемой на некотором промежутке, достаточно,
чтобы она имела на нём непрерывную производную порядка n.
2.
Дифференциалы высших порядков
Пусть функция ![]() дифференцируема на
некотором интервале
дифференцируема на
некотором интервале ![]() . Как известно, её дифференциал
. Как известно, её дифференциал ![]() , который называется также её первым дифференциалом, зависит
от двух переменных: x и dx. Пусть функция
, который называется также её первым дифференциалом, зависит
от двух переменных: x и dx. Пусть функция ![]() , в свою очередь, дифференцируема в некоторой точке
, в свою очередь, дифференцируема в некоторой точке ![]() . Тогда дифференциал в этой точке функции dy, рассматриваемой как функция только от x (т. е. при некотором фиксированном dx), имеет вид
. Тогда дифференциал в этой точке функции dy, рассматриваемой как функция только от x (т. е. при некотором фиксированном dx), имеет вид ![]() и называется вторым дифференциалом функции f в этой точке и обозначается через
и называется вторым дифференциалом функции f в этой точке и обозначается через ![]() .
.
Подобным же образом в том случае, когда производная (n–1)-го порядка ![]() , дифференцируема в точке x0 или, что эквивалентно, когда при x=x0 существует производная n-го порядка
, дифференцируема в точке x0 или, что эквивалентно, когда при x=x0 существует производная n-го порядка ![]() , определяется дифференциал n-го порядка
, определяется дифференциал n-го порядка ![]() функции
функции ![]() в точке x0 как дифференциал от дифференциала (n–1)-го порядка
в точке x0 как дифференциал от дифференциала (n–1)-го порядка ![]() :
: ![]() , т. е.
, т. е.  .
.
3.
Формула Тейлора.
Теорема. Пусть функция ![]() , определённая на интервале
, определённая на интервале ![]() , имеет в точке
, имеет в точке ![]() производные до порядка
n включительно. Тогда при x®x0
производные до порядка
n включительно. Тогда при x®x0  .
.
Эта формула называется
формулой Тейлора n-го порядка с остаточным членом в
форме Пеано.
Многочлен  называется многочленом Тейлора степени n, а функция
называется многочленом Тейлора степени n, а функция ![]() – остаточным членом n-го порядка формулы Тейлора.
– остаточным членом n-го порядка формулы Тейлора.
Если в этой формуле
положить x0 = 0, то получается частный вид
формулы Тейлора, называемый обычно формулой
Маклорена:  .
.
Доказанная теорема позволяет любую функцию, удовлетворяющую
условиям этой теоремы, заменить в окрестности некоторой точки многочленом с
точностью до бесконечно малых более высокого порядка, чем члены многочлена.
Таким многочленом является многочлен Тейлора. Величина погрешности определяется
при этом остаточным членом.
Замечание. Можно показать, что если функция ![]() в некоторой
окрестности точки x0 имеет производную порядка n, то, какова бы ни была точка x этой окрестности, найдётся такая
точка x, лежащая между x0 и x, что для остаточного члена
в некоторой
окрестности точки x0 имеет производную порядка n, то, какова бы ни была точка x этой окрестности, найдётся такая
точка x, лежащая между x0 и x, что для остаточного члена ![]() формулы Тейлора
функции
формулы Тейлора
функции ![]() имеет место формула
имеет место формула  (форма Лагранжа),
(форма Лагранжа),  (форма Коши).
(форма Коши).
Тема
8. Исследование поведения функций с помощью производных
1.
Асимптоты плоской кривой
Определение 1. Если точка M(x; y) перемещается по кривой y =
f(x) так, что хотя бы одна из
координат точки стремится к ¥ и при этом расстояние от этой точки до некоторой
прямой стремится к 0, то эта прямая называется асимптотой кривой y = f(x).
Асимптоты бывают двух видов: вертикальные и наклонные.
Определение 2. Прямая x = a называется вертикальной асимптотой кривой y = f(x), если хотя
бы один из односторонних пределов ![]() или
или ![]() равен +¥ или
– ¥.
равен +¥ или
– ¥.
Замечание.
Если прямая x =
a является вертикальной асимптотой кривой y = f(x), то в
точке x =
a функция f(x) имеет
разрыв второго рода. Наоборот, если в точке x = a функция f(x) имеет разрыв второго рода, то прямая x = a является
вертикальной асимптотой кривой y = f(x).
Определение 3. Прямая ![]() называется наклонной асимптотой кривой
называется наклонной асимптотой кривой ![]() при
при ![]() (или
(или ![]() ), если функцию f(x) можно
представить в виде:
), если функцию f(x) можно
представить в виде:
![]() ,
,
где ![]() (x) – бесконечно малая функция при
(x) – бесконечно малая функция при ![]() (или
(или ![]() ).
).
Теорема 1. Для того
чтобы кривая y =
f(x) имела
наклонную асимптоту при ![]() (или
(или![]() ) необходимо и достаточно существования
двух конечных пределов:
) необходимо и достаточно существования
двух конечных пределов:
 и
и 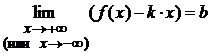
Доказательство. Ограничимся случаем ![]() .
.
Необходимость. Пусть y = kx+b – наклонная асимптота при ![]() кривой y = f(x). Тогда
функцию f(x) представим в виде:
кривой y = f(x). Тогда
функцию f(x) представим в виде:
![]() , где
, где ![]() при
при ![]() .
.
Убедимся в существовании конечных пределов:
 .
.
![]() .
.
Необходимость доказана.
Достаточность.
Пусть существуют конечные пределы  и
и ![]() .
.
Тогда по свойству конечных пределов
второй предел можно переписать в виде:
![]() ,
,
где ![]() (x) – бесконечно малая величина при
(x) – бесконечно малая величина при ![]() .
.
Отсюда получаем:![]() , где
, где ![]() при
при ![]() .
.
Достаточность доказана.
Пример 1.
Найти асимптоты кривой  .
.
Решение.
1) D(y) = (–¥;–1) È (–1;1) È (1;+ ¥).
2) Точки x = –1 и x =
1 являются точками разрыва второго рода, так как:
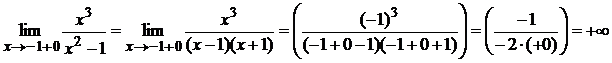
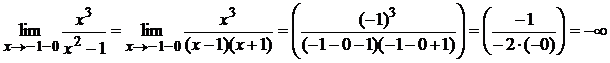
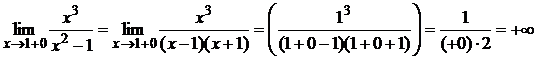
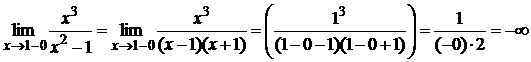
Поэтому прямые
x =
–1 и x =
1 являются вертикальными асимптотами.
3) Вычислим пределы:
 , k =
1.
, k =
1.
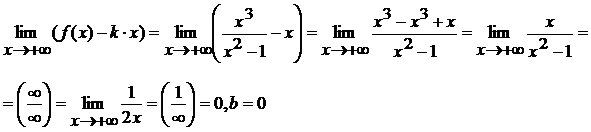
Отсюда следует, что при ![]() прямая y = 1×x +0, т.е. y = x –
наклонная асимптота при
прямая y = 1×x +0, т.е. y = x –
наклонная асимптота при ![]() .
.
Найдём наклонную асимптоту при ![]() .
.
Вычисляя те же пределы при ![]() , получим k = 1 и b = 0, т.е. прямая y = x является наклонной
асимптотой при
, получим k = 1 и b = 0, т.е. прямая y = x является наклонной
асимптотой при ![]() .
.
Ответ: x = ± 1 –
вертикальные асимптоты, y = x –
наклонная асимптота при x ® ±¥.
2.
Монотонность функции
Определение 4. Функция y = f(x) называется
возрастающей (убывающей) на
промежутке (a;b), если для
любых x1 и x2, принадлежащих этому промежутку, из условия x2
> x1 следует неравенство:
f(x2) > f(x1) (f(x2) < f(x1)).
Определение 5. Функция y = f(x) называется
монотонной на промежутке (a;b), если она на этом промежутке
является только возрастающей или только убывающей.
Теорема 2 (достаточные условия
монотонности). Если
функция y =
f(x)
дифференцируема на промежутке (a;b) и f’(x) > 0 (f’(x) < 0)
для любых x Î (a;b), то
функция возрастает (убывает) на этом промежутке.
Доказательство.
Возьмём любые два значения x1 и x2 из промежутка (a;b). Для определённости предположим, что x2 > x1.
На отрезке [x1;x2] функция y =
f(x) непрерывна
и дифференцируема (из условия теоремы). Следовательно, она удовлетворяет
теореме Лагранжа на отрезке [x1; x2], т.е. существует хотя бы одна точка c Î (x1; x2), в которой выполняется равенство:
f(x2) – f(x1) = f' (c) × (x2 – x1).
Если f '(x) > 0 для
любых xÎ(a;b), то f '(c) > 0. Поэтому f(x2) – f(x1) > 0, т.е. из условия x2 > x1 следует неравенство f(x2) > f(x1). А так как x1 и x2
–любые
значения из промежутка (a;b), то
функция y =
f(x) возрастает
на этом промежутке.
Если ![]() для любых
для любых ![]() , то
, то ![]() . Поэтому
. Поэтому![]() , то есть из условия x2 > x1 следует неравенство f(x2) < f(x1). Так как x1 и x2 любые значения из промежутка (a;b), то функция y = f(x) убывает на
этом промежутке.
, то есть из условия x2 > x1 следует неравенство f(x2) < f(x1). Так как x1 и x2 любые значения из промежутка (a;b), то функция y = f(x) убывает на
этом промежутке.
Теорема доказана.
3.
Экстремумы функции
Определение 6. Функция y = f(x) имеет в
точке x0ÎD(f) максимум
ymax (минимум
ymin), если существует такая окрестность
точки x0, в которой для всех x выполняется неравенство:
f(x0) > f(x) (f(x0) < f(x)).
Определение 7. Точки
максимума и минимума функции называются точками экстремума функции.
Теорема 3 (необходимое условие
экстремума). Если
функция y =
f(x) имеет
экстремум в точке x0, то в этой точке производная функции равна нулю или
не существует.
Доказательство. 1)Для определённости рассмотрим случай, когда функция y = f(x) в точке x0 имеет максимум и в этой точке существует производная.
Тогда из определения максимума для любого x,
принадлежащего окрестности точки x0
f(x0) > f(x).
Отсюда следует, что для любого Dx ≠ 0 справедливо
неравенство: f(x0+Dx) – f(x0) < 0. Разделим это неравенство на
Dx,
получим: при Dx > 0: ![]() при Dx < 0:
при Dx < 0: ![]()
Перейдём к пределам: ![]()
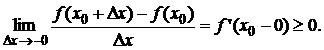
Так как![]() существует, то:
существует, то: ![]()
Аналогично рассматривается случай,
когда x0 – точка минимума.
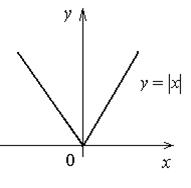
2) Если f '(x0) не существует или равна ¥, то
точка x0 может быть точкой экстремума функции.
Например, функция y = ![]() имеет минимум при x = 0, хотя y'(0) не
существует (рис. 9).
имеет минимум при x = 0, хотя y'(0) не
существует (рис. 9).
Теорема доказана.
Теорема 4 (достаточное условие
экстремума). Если
функция y =
f(x) непрерывна
в точке x0, дифференцируема в некоторой её окрестности, за
исключением может быть самой этой точки, f’(x0) = 0 или не существует и при переходе x через точку x0 производная f '(x) изменяет знак, то точка x0 является точкой экстремума. Если при этом знак
f '(x) меняется
с + на –, то x0 – точка максимума,
с
– на +, то x0 – точка минимума.
Доказательство.
Пусть f '(x) при переходе x через точку
x0 изменяет знак с
+
на – ,
т.е. f '(x) > 0 при x Î
(x0 – d; x0) и
f '(x) <
0 при x Î (x0; x0 + d),
где d > 0
(рис. 10).
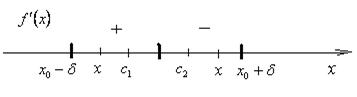
1) Пусть x Î (x0 – d; x0). На отрезке [x; x0] функция y =
f(x)
удовлетворяет теореме Лагранжа. Значит, на интервале (x; x0) найдётся хотя бы одна точка c1, в которой выполняется равенство: f(x) – f(x0) = f '(c1)×(x –
x0), где c1Î (x0 – d; x0).
Так как f '(c1) > 0 и x – x0 < 0, то f(x) – f(x0) < 0.
2) Пусть ![]() . На отрезке
. На отрезке ![]() функция
функция ![]() также удовлетворяет
теореме Лагранжа. Значит на интервале (x0; x) найдётся
хотя бы одна точка с2, в которой выполняется равенство: f(x) – f(x0) = f’(c2)×(x – x0),
также удовлетворяет
теореме Лагранжа. Значит на интервале (x0; x) найдётся
хотя бы одна точка с2, в которой выполняется равенство: f(x) – f(x0) = f’(c2)×(x – x0),
где c2 Î (x0; x0 + d). Так как f '(c2) < 0 и x –
x0
> 0, то f(x) – f(x0) < 0.
Следовательно, для любого x Î (x0 – d; x0 + d) выполняется неравенство: f(x0) > f(x).
Отсюда следует, что точка x0 является точкой
максимума функции y =
f(x). Аналогично рассматривается случай, когда ![]() при переходе x через точку x0 изменяет знак с – на +. При этом точка x0 является точкой минимума функции
при переходе x через точку x0 изменяет знак с – на +. При этом точка x0 является точкой минимума функции ![]() .
.
Теорема доказана.
4.
Выпуклость, вогнутость и точки перегиба графика функции
Пусть функция y = f(x) дифференцируема в любой точке промежутка (a;b). Тогда она имеет конечную
производную в любой точке этого промежутка. Значит, существует касательная к
графику функции y =
f(x) в любой
его точке (x; f(x)) при a <
x <
b.
Определение 8. График функции y = f(x), дифференцируемой в каждой точке промежутка (a;b), называется выпуклым (вогнутым) на этом промежутке, если для любого x Î (a;b) график расположен не выше (не ниже)
касательной к графику в точке (x; f(x)).
Теорема 5 (достаточное условие
выпуклости или вогнутости кривой).
Пусть функция y = f(x) дважды дифференцируема на промежутке (a;b) и
f ''(x) для x Î (a;b) сохраняет свой знак, тогда кривая y = f(x) выпуклая,
если f ''(x) £ 0
при x Î (a;b), и кривая y =
f(x) вогнутая, если f ''(x) ³ 0
при x Î (a;b).
Доказательство.
Для определённости рассмотрим случай, когда f ''(x) ³ 0 для x Î (a;b). Обозначим x0 любую точку промежутка (a;b). Построим касательную к кривой y = f(x) в точке (x0; f(x0)): yкасат = f(x0) + f '(x0)∙(x –
x0). Покажем, что график функции y = f(x) лежит не ниже этой касательной,
т.е. выполняется неравенство: (f(x) – yкасат(x)) ³ 0 для любого x Î (a;b).
f(x) – yкасат(x) = f(x) – (f(x0) + f '(x0)∙(x –
x0)) =
= f(x)
– f(x0) – f '(x0)∙(x – x0)
= (f(x) – f(x0)) – f '(x0)∙(x – x0), где x Î (a;b) . (1)
Функция y = f(x) на отрезке
[x0;x] удовлетворяет условию теоремы
Лагранжа, т.е. на отрезке [x0;x] найдётся хотя бы одна точка c1, для которой выполняется равенство: f (x) – f(x0) =
f '(c1)∙(x – x0).
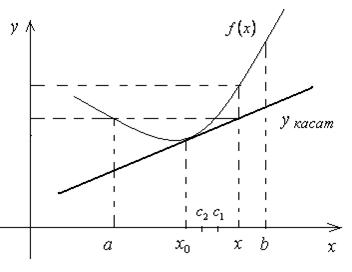
Подставим в равенство (1) полученное
соотношение.
f(x) –
yкасат(x) = f '(c1)(x– x0) – f ' (x0)(x –
x0) = (x – x0)×(f ' (c1) – f ' (x0)). (2) Функция f '(x) на отрезке
[x0;c1]
удовлетворяет условию теоремы Лагранжа, т.е. на промежутке (x0;c1) найдётся хотя бы одна точка с2, для которой выполняется
равенство:
f
'(c1) – f '(x0)
= f
''(c2)(c1 – x0).
Подставим в равенство (2) полученное
соотношение:
f(x) – yкасат(x) = (x –
x0)×f ''(c2)∙(c1 – x0). (3)
Если x > x0, то c1 > x0 и c2 > x0, т.е. x – x0 > 0 и с1
– x0 > 0.
По предположению f ''(x) ³ 0. Тогда f(x) – yкасат(x) ³ 0.
Если x < x0, то c1 < x0 и
c2 < x0, т.е. x – x0 < 0 и c1 – x0 < 0. Тогда f(x) – yкасат(x) ³ 0.
Следовательно, при любом x Î (a;b) выполняется неравенство: f(x) – yкасат(x) ³ 0, т.е. на промежутке (a,b) график функции y = f(x) вогнутый.
Аналогично можно доказать, что если f ''(x) £ 0 при любом x Î (a;b), то кривая y = f(x) на промежутке
(a;b) будет
выпуклой.
Теорема доказана.
Определение 9. Пусть в
точке (x0; f(x0)) существует касательная. Тогда точка
(x0; f(x0)), отделяющая выпуклую часть кривой
от вогнутой (или наоборот) называется точкой
перегиба графика функции y =
f(x).
Теорема 6 (достаточное условие точки
перегиба). Если
функция y =
f(x) дважды
дифференцируема в окрестности точки x0, вторая производная функции f ''(x0) = 0 (или не существует) и f ''(x) меняет свой знак при переходе x через точку x0, то точка (x0; f(x0)) – точка перегиба кривой y =
f(x).
Доказательство.
Для определенности рассмотрим случай, когда f ''(x) при переходе через точку x0 изменяет знак с
+ на
–.
Тогда в левой полуокрестности точки x0 f ''(x) > 0, т. е. кривая при x < x0 вогнутая, а в правой полуокрестности точки x0 f ''(x) < 0, т. е. кривая при x > x0 выпуклая.
Следовательно, точка (x0; f(x0)) по определению является точкой
перегиба графика функции y = f(x).
Аналогично рассматривается другой
случай, когда f ''(x) при
переходе через точку x0 изменяет знак с – на
+.
Теорема доказана.
5.
Наибольшее и наименьшее значения функции на отрезке
Пусть функция y = f(x) определена на отрезке [a;b].
Определение 10. Число f(c) называется
наибольшим (наименьшим) значением функции y = f(x) на отрезке
[a;b] и
обозначается ![]() (
(![]() ), если для любого x Î
[a;b]
выполняется неравенство: f(x) £ f(c)
(f(x) ³ f(c)) .
), если для любого x Î
[a;b]
выполняется неравенство: f(x) £ f(c)
(f(x) ³ f(c)) .
Если функция y = f(x) непрерывна на отрезке [a;b], то по свойству непрерывной на
отрезке функции она достигает
своих наибольшего и наименьшего значений.
Схема нахождения этих значений
следующая:
1) Найти все точки, в которых f '(x) = 0 (или
не существует). Причём выбрать те точки из полученных,
которые попадают на отрезок [a;b].
2) Вычислить значения функции в
полученных точках в п.1.
3) Вычислить значения функции в
граничных точках отрезка [a;b]: f(a) и f(b).
4) Из значений п.2 и п.3 найти
наибольшее число M и наименьшее m.
Тогда ![]()
![]()
6.
Схема исследования функции. Построение графика
1) Найти область определения функции y = f(x) –
множество D(f) тех
значений x, при которых функция y = f(x) имеет смысл.
2) Исследовать функцию на периодичность: выяснить, существует ли
наименьшее положительное число T такое, что f(x+T) = f(x) для любого
xÎ D(f). Если «да», то целесообразно далее
исследовать функцию и строить её график только на некотором отрезке длиной
периода T. Затем продолжить график на всю
область определения, разбивая её на интервалы длины T, в которых
повторяется картинка графика.
3)
Исследовать функцию на чётность и нечётность: выяснить, выполняются ли равенства:
f(– x) = f(x) для любого xÎ D(f) – чётность
или
f(– x) = – f(x) для любого xÎ D(f) – нечётность.
Это позволяет узнать, есть ли
симметрия графика: относительно оси Oy – чётная или относительно начала координат – нечётная.
4) Найти точки пересечения графика
функции![]() с осями координат:
с осями координат:
· с осью Oy: точка (0; f(0)), если 0 Î D(f),
· с осью Oх: точка (xk; 0), где xkÎ D(f) и является решением уравнения f(x) = 0.
5) Найти промежутки знакопостоянства:
выяснить, при каких x Î D(f) выполняются неравенства f(x) > 0 (график функции расположен выше оси Ox) и f(x) < 0
(график функции расположен ниже оси Ox).
6) Исследовать функцию на непрерывность, установить тип точек разрыва.
7) Найти вертикальные и
наклонные асимптоты (см. §6, п.1, с. 43).
8) Найти промежутки убывания и возрастания, экстремумы функции.
9) Найти множество E(f) значений функции.
10) Найти промежутки выпуклости, вогнутости и точки перегиба графика.
11) Построить график функции, используя свойства, установленные в
проведенном исследовании. Если в некоторых промежутках график остался неясным,
то его уточняют по дополнительным точкам.
Пример.
Исследовать функцию y =
(x +
2)e–x и построить её
график.
1) D(y) = R.
2) Функция не периодическая.
3) Так как y(–x) ≠ y(x) и y(–x) ≠ –y(x), то функция общего вида, не
является ни чётной, ни нечётной.
4) Точка пересечения графика с осью Ox : (– 2; 0), с Oy : (0; 2)
5) При x Î (–¥; –2) функция отрицательная, при x Î (–2; +¥) функция положительная.
6) Функция непрерывна при x Î R.
7) Вертикальных асимптот нет.
Наклонные асимптоты: y = kx +
b.
а) 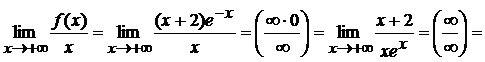
 k = 0
при x ® +¥
k = 0
при x ® +¥
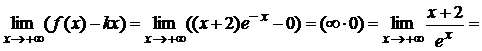
![]()
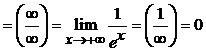
b = 0 при ![]() .
.
Следовательно, y = 0 – наклонная (горизонтальная)
асимптота при ![]() .
.
б) ![]()
при ![]() наклонной асимптоты
нет.
наклонной асимптоты
нет.
8) f '(x) = ((x + 2)e– x) ' = 1×e– x+(x + 2)×(–e–x) = e–x(1 – x – 2) = –(x + 1)e– x.
D(y') = R.
 y ' = 0: – (x+1)e– x = 0 Þ x = – 1,
f(–1) = 1×e1 =
e.
y ' = 0: – (x+1)e– x = 0 Þ x = – 1,
f(–1) = 1×e1 =
e.
при x Î (– ¥;– 1) f(x) возрастает, при x Î(– 1;+¥) f(x) убывает,
при x = –1 fmax (– 1) = (– 1+2)e– (– 1) = e.
9) E(f) = (–¥; e), так как
![]()
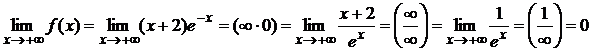
 и
fmax (–1) = e.
и
fmax (–1) = e.
10) f ''(x) = (– (x + 1)e– x) ' = – 1e– x + (x +
1)e–x = e– x(x +
1 – 1) = xe–x.
D(f '') = R
f
'' (x) = 0 : xe– x = 0 Þ x = 0,
f(0) = 2.
при x Î
(– ¥;0) график f(x) выпуклый,
при x Î
(0;+¥) график f(x) вогнутый. Точка (0;2) – точка перегиба
графика.
11) Результаты проведенного исследования cведём в таблицу и построим график
Результаты исследования функции y = (x + 2)e – x
|
x |
(– ¥;–
1) |
–
1 |
(– 1;0) |
0 |
(0;+¥) |
|
знак f
' (x) |
+ |
0 |
– |
– |
– |
|
знак f '' (x) |
– |
– |
– |
0 |
+ |
|
F(x) |
|
e |
|
2 |
|
|
|
|
|
|
|
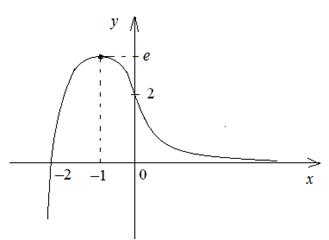
Модуль
3
Тема
9. Понятие сходимости в конечномерном пространстве
Определение
функции двух и более переменных
Пусть дано некоторое множество ![]() упорядоченных пар
чисел
упорядоченных пар
чисел ![]() .
.
Величина ![]() называется функцией
двух переменных
называется функцией
двух переменных ![]() и
и ![]() , если существует правило или закон, по которому каждой паре
чисел
, если существует правило или закон, по которому каждой паре
чисел ![]() соответствует вполне
определенное значение
соответствует вполне
определенное значение ![]() .
.
Переменные ![]() и
и ![]() называются
независимыми переменными или аргументами. Область
называются
независимыми переменными или аргументами. Область ![]() называется областью определения функции.
называется областью определения функции.
Обозначение функции двух переменных:
![]() ,
, ![]() ,
, ![]() и т.д.
и т.д.
Функцию ![]() можно рассматривать
как функцию точки
можно рассматривать
как функцию точки ![]() плоскости
плоскости ![]() и обозначить
и обозначить ![]() .
.
Значение функции ![]() в точке
в точке ![]() обозначают
обозначают ![]() ,
, ![]() .
.
Переменная величина ![]() называется функцией нескольких независимых переменных, если
каждой системе значений
называется функцией нескольких независимых переменных, если
каждой системе значений ![]() этих переменных из
данной области их значения соответствует единственное значение величины
этих переменных из
данной области их значения соответствует единственное значение величины ![]() .
.
Обозначение: ![]() ,
, ![]() - аргументы функции.
- аргументы функции.
Областью определения ![]() функции
функции ![]() ,
, ![]() может быть вся
плоскость или ее часть, ограниченная некоторыми линиями – границами области.
Точки области, не лежащие на границе, называются внутренними.
может быть вся
плоскость или ее часть, ограниченная некоторыми линиями – границами области.
Точки области, не лежащие на границе, называются внутренними.
Область называется открытой, если она состоит только из внутренних точек.
Область с присоединенной к ней границей
называется замкнутой и обозначается ![]() .
.
Область называется ограниченной, если существует такое число ![]() , что расстояние любой точки
, что расстояние любой точки ![]() области от начала
координат меньше
области от начала
координат меньше ![]() , т.е.
, т.е. ![]()
Пример1. Найти область
определения функции ![]() .
.
Решение. Для того,
чтобы значения функции ![]() были действительными
числами, подкоренное выражение должно быть неотрицательным, т.е.
были действительными
числами, подкоренное выражение должно быть неотрицательным, т.е.
![]() или
или ![]() .
.
Уравнением границы области является
окружность ![]() .
. ![]() - замкнутая,
ограниченная область.
- замкнутая,
ограниченная область.
Геометрическое изображение функции двух
переменных
Изобразим в плоскости ![]() область определения
функции
область определения
функции ![]() . В каждой точке
. В каждой точке ![]() восстановим
перпендикуляр к плоскости
восстановим
перпендикуляр к плоскости ![]() и отложим на нем
значение функции
и отложим на нем
значение функции ![]() .
.
Геометрическое место всех точек ![]() есть некоторая
поверхность, которая является геометрическим изображением функции
есть некоторая
поверхность, которая является геометрическим изображением функции ![]() .
.
Существует способ изображения функции двух
переменных, основанный на сечении поверхности ![]() плоскостями
плоскостями ![]() , где
, где ![]() - любое число.
- любое число.
Линией
уровня функции ![]() называется множество
точек
называется множество
точек ![]() плоскости
плоскости ![]() , в которых функция принимает одно и то же значение
, в которых функция принимает одно и то же значение ![]() . При различных
. При различных ![]() получаются различные
линии уровня для данной функции.
получаются различные
линии уровня для данной функции.
Тема 10. Пределы и непрерывность функции многих переменных
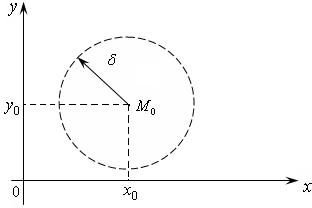
![]() -окрестностью точки
-окрестностью точки ![]() называется множество
всех точек
называется множество
всех точек ![]() плоскости, координаты
которых удовлетворяют неравенству:
плоскости, координаты
которых удовлетворяют неравенству:
![]() .
.
Пусть ![]() определена в некоторой
окрестности точки
определена в некоторой
окрестности точки ![]() , кроме быть может, самой этой
точки.
, кроме быть может, самой этой
точки.
Число ![]() называется пределом функции
называется пределом функции ![]() при
при
![]() и
и ![]() (т.е. при
(т.е. при ![]() ), если для любого
), если для любого ![]() существует
существует ![]() такое, что для всех
такое, что для всех ![]() и
и ![]() удовлетворяющих
неравенству
удовлетворяющих
неравенству ![]() будет выполняться
неравенство
будет выполняться
неравенство
![]() .
.
Обозначение: ![]() или
или ![]() .
.
Основные свойства предела
функции двух переменных аналогичны свойствам предела функции одной переменной.
Теорема. Если функции ![]() и
и ![]() определены на множестве
определены на множестве ![]() и имеют в точке
и имеют в точке ![]() этого множества
пределы
этого множества
пределы ![]() и
и ![]() соответственно, то и
функции
соответственно, то и
функции ![]() ,
, ![]() ,
,  имеют в точке
имеют в точке ![]() пределы, которые
соответственно равны
пределы, которые
соответственно равны ![]() ,
, ![]() ,
, ![]() .
.
Функция ![]() называется бесконечной малой в точке
называется бесконечной малой в точке ![]() , если
, если ![]() .
.
Замечание. Из
существования предела функции вдоль некоторой кривой, соединяющей точки ![]() и
и ![]() , вообще говоря, не следует существования предела функции в
точке
, вообще говоря, не следует существования предела функции в
точке ![]() , но он будет существовать в том случае, когда существует
предел по любой кривой, соединяющей точки
, но он будет существовать в том случае, когда существует
предел по любой кривой, соединяющей точки ![]() и
и ![]() , и все эти пределы равны между собой.
, и все эти пределы равны между собой.
Функция ![]() (или функция
(или функция ![]() ) называется непрерывной в
точке
) называется непрерывной в
точке ![]() , если:
, если:
1) ![]() определена
в этой точке и некоторой её окрестности,
определена
в этой точке и некоторой её окрестности,
2) ![]() имеет предел
имеет предел ![]() ,
,
3) этот предел равен значению функции ![]() в точке
в точке ![]() , т.е.
, т.е. ![]() или
или ![]() . Обозначим
. Обозначим 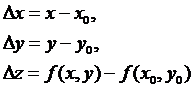
![]() ,
, ![]() - приращения аргументов
- приращения аргументов ![]() и
и ![]() .
.
![]() - полное приращение
функции
- полное приращение
функции ![]() в точке
в точке ![]()
Функция ![]() называется непрерывной в точке
называется непрерывной в точке ![]() , если
, если ![]() .
.
Функция ![]() называется непрерывной в некоторой области, если она
непрерывна в каждой точке этой области.
называется непрерывной в некоторой области, если она
непрерывна в каждой точке этой области.
Точки, в которых функция
не является непрерывной, называются точками
разрыва этой функции.
Теорема. Если функция ![]() непрерывна в
ограниченной замкнутой области
непрерывна в
ограниченной замкнутой области ![]() , то она в этой области:
, то она в этой области:
1) ограничена, т.е.
![]()
![]() ,
, ![]() .
.
2) имеет точки, в которых принимает наименьшее ![]() и наибольшее
и наибольшее ![]() значения.
значения.
3) принимает хотя бы в одной точке области любое
численное значение, заключенное между значениями ![]() и
и ![]() .
.
Тема 11. Частные производные и дифференциалы
Пусть ![]() определена
в некоторой окрестности точки
определена
в некоторой окрестности точки ![]() .
.
Дадим переменной ![]() в точке
в точке ![]() приращение
приращение ![]() , а переменную
, а переменную ![]() оставим без изменения.
Тогда функция
оставим без изменения.
Тогда функция ![]() получит приращение
получит приращение ![]() .
. ![]() называется частным приращением
называется частным приращением ![]() по
по
![]() в точке
в точке ![]() .
.
Аналогично получаем частное приращение ![]() по
по
![]() :
: ![]() .
.
Если существует предел
![]() ,
,
то он называется частной
производной функции ![]() в точке
в точке ![]() по переменной
по переменной ![]() и обозначается
и обозначается ![]() .
.
Итак, ![]() .
.
Аналогично определяется частная
производная от функции ![]() по переменной
по переменной ![]() в точке
в точке ![]() .
.
 .
.
Частные производные функции ![]() находят по формулам
вычисления производных функции одной переменной, при этом другая переменная
считается постоянной.
находят по формулам
вычисления производных функции одной переменной, при этом другая переменная
считается постоянной.
Примеры. Для указанных
функций найти частные производные.
1) ![]() .
.
![]() ,
,  .
.
2) ![]() .
.
![]() ,
,  .
.
Понятие дифференцируемости функции
Пусть функция ![]() определена в некоторой
окрестности точки
определена в некоторой
окрестности точки ![]() , тогда полное приращение этой функции в точке М имеет вид:
, тогда полное приращение этой функции в точке М имеет вид:
![]() .
.
Функция ![]() называется дифференцируемой в точке
называется дифференцируемой в точке ![]() , если её полное приращение в этой точке можно представить в
виде
, если её полное приращение в этой точке можно представить в
виде
![]() ,
,
где ![]() и
и ![]() при
при ![]() и
и ![]() .
.
Теорема (необходимое условие
дифференцируемости функции).
Если функция ![]() дифференцируема в точке
дифференцируема в точке ![]() , то она непрерывна
в этой точке, имеет в ней частные производные
, то она непрерывна
в этой точке, имеет в ней частные производные ![]() и
и ![]() , причем
, причем ![]() ,
,  .
.
Теорема (достаточное условие дифференцируемости функции).
Если функция ![]() имеет непрерывные
частные производные
имеет непрерывные
частные производные ![]() и
и ![]() в точке, то она
дифференцируема в этой точке.
в точке, то она
дифференцируема в этой точке.
Известно, если функция дифференцируема в
точке ![]() , то имеет место соотношение
, то имеет место соотношение
![]() ,
,
где ![]() - бесконечно малые
функции при
- бесконечно малые
функции при ![]() и
и ![]() .
.
Главная линейная часть относительно ![]() и
и ![]() полного приращения
функции Δz в точке
полного приращения
функции Δz в точке ![]() называется полным дифференциалом функции
называется полным дифференциалом функции ![]() и обозначается:
и обозначается: ![]() .
.
Теорема. Если ![]() дифференцируема
в точке
дифференцируема
в точке ![]() , то её полный дифференциал равен:
, то её полный дифференциал равен:  .
.
Частные производные и дифференциалы высших
порядков
Пусть функция ![]() в некоторой области
в некоторой области ![]() имеет частные
производные
имеет частные
производные
![]() и
и  .
.
Будем называть их частными
производными первого порядка.
Частные производные первого порядка можно
рассматривать как функции от двух переменных ![]() и
и ![]() . Если эти функции дифференцируемы в точке
. Если эти функции дифференцируемы в точке ![]() области
области ![]() , то их частные производные называются частными производными второго порядка и
обозначаются следующим образом:
, то их частные производные называются частными производными второго порядка и
обозначаются следующим образом:
 ,
,  ,
,  ,
,  .
.
Производные ![]() и
и ![]() называются смешанными частными производными.
называются смешанными частными производными.
Теорема. Если функция ![]() имеет в точке
имеет в точке ![]() и ее окрестности
непрерывные смешанные производные
и ее окрестности
непрерывные смешанные производные ![]() и
и ![]() , то они в этой точке равны, т.е.
, то они в этой точке равны, т.е. ![]() =
=![]() .
.
Аналогично определяются частные
производные третьего, четвертого и т.д. порядков. Например,  ,
,  .
.
Дифференциалы второго, третьего и т.д.
порядков от функции ![]() определяются
формулами
определяются
формулами ![]() ,
, ![]() и т.д.
и т.д.
 .
.
Тема 12. Задачи на экстремум функций многих переменных
Экстремум функции многих переменных
рассмотрим на функции двух переменных.
Точка ![]() называется точкой максимума (минимума) функции
называется точкой максимума (минимума) функции ![]() , если существует такая
, если существует такая ![]() -окрестность точки
-окрестность точки ![]() , для всех точек которой выполняется неравенство:
, для всех точек которой выполняется неравенство: ![]() или
или ![]() (
(![]() ,
, ![]() ) .
) .
Точки максимума и минимума называются точками экстремума (экстремальными точками),
а значение функции в такой точке называется экстремумом функции.
Теорема (необходимый признак экстремума
дифференцируемой функции). Если функция ![]() дифференцируема в точке
дифференцируема в точке ![]() и достигает в ней
экстремум, то все её частные производные первого порядка в этой точке равны
нулю, т.е.
и достигает в ней
экстремум, то все её частные производные первого порядка в этой точке равны
нулю, т.е.
 .
.
Точка ![]() называется стационарной точкой для функции
называется стационарной точкой для функции ![]() , если её частные производные первого порядка в этой точке
равны нулю.
, если её частные производные первого порядка в этой точке
равны нулю.
Отсюда следует, что всякая экстремальная
точка дифференцируемой функции будет и стационарной. Обратное утверждение
неверно, т.е. не всякая стационарная точка является точкой экстремума.
Например, точка ![]() является стационарной
для функции
является стационарной
для функции ![]() , но
, но ![]() не является
экстремумом, т.к. в любой окрестности точки
не является
экстремумом, т.к. в любой окрестности точки ![]() будут находиться как
точки в окрестности
будут находиться как
точки в окрестности ![]() , так и точки в окрестности
, так и точки в окрестности ![]() .
.
В точке
экстремума функция не обязательно должна быть дифференцируемой.
Например, в точке ![]() функция
функция ![]() имеет минимум, однако
её частные производные в этой точке не существуют.
имеет минимум, однако
её частные производные в этой точке не существуют.
Следствие. Точками экстремума могут
быть либо стационарные точки, либо точки, в которых функция не дифференцируема.
Все эти точки
называются критическими и
только они являются «подозрительными» на экстремум.
Все
сказанное обобщается на функцию любого числа переменных.
Рассмотрим достаточный признак экстремума
дифференцируемой функции.
Пусть точка ![]() является стационарной, причем в этой точке и
некоторой её
является стационарной, причем в этой точке и
некоторой её ![]() -окрестности функция
-окрестности функция ![]() имеет частные
производные до второго порядка включительно.
имеет частные
производные до второго порядка включительно.
Введем обозначения значений частных
производных второго порядка в точке ![]() . Пусть
. Пусть
 ,
,  ,
,  .
.
Обозначим
![]() .
.
Теорема 1. Если в
стационарной точке ![]()
![]() > 0, то функция
> 0, то функция ![]() в точке
в точке ![]() имеет
экстремум, причем при
имеет
экстремум, причем при ![]() – max, при
– max, при ![]() – min.
– min.
Теорема 2. Если в стационарной точке ![]()
![]() < 0, то функция
< 0, то функция ![]() в точке
в точке ![]() экстремума не
имеет.
экстремума не
имеет.
Замечание.
Если в стационарной точке ![]()
![]() = 0, то вопрос о наличии экстремума в ней остается открытым.
= 0, то вопрос о наличии экстремума в ней остается открытым.
Схема
исследования функции двух переменных ![]() на экстремум.
на экстремум.
1. Найти стационарные
(критические) точки ![]() .
.
1) Найти ![]() ,
, ![]() .
.
2) Решить систему: 
Пусть ![]() и
и ![]() – решения
системы, тогда
– решения
системы, тогда ![]() и
и ![]() - стационарные
точки.
- стационарные
точки.
2. Проверим точки на
экстремум с помощью достаточного условия.
3. Найдем ![]() ,
, ![]() ,
, ![]() .
.
Для каждой стационарной точки найдем значения
![]() ,
, ![]() ,
, ![]() ,
, ![]() (например, для точки
(например, для точки ![]() ).
).
 ,
,  ,
,  .
.
4. Вычислим ![]() .
.
5.
Для определения точек экстремума воспользуемся
следующей таблицей
|
D |
А |
Вывод |
|
+ |
+ |
min |
|
+ |
– |
max |
|
– |
|
экстремума
нет |
|
0 |
|
дополнительное
исследование |
Пример
13.2.
Исследовать на экстремум функцию
![]() .
.
Решение.
1) ![]() ,
,  .
.
2) 




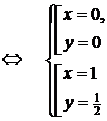
![]() и
и ![]() - стационарные
точки.
- стационарные
точки.
3)  ,
,  ,
,  .
.
4) Для точки ![]() :
:
 ,
,  ,
,  .
.
Так как ![]() , в точке
, в точке ![]() экстремума нет.
экстремума нет.
Для точки ![]() имеем:
имеем:
 ,
,  ,
,  .
.
![]() .
.
Так как ![]() и
и ![]() , то в точке
, то в точке ![]() функция имеет минимум,
функция имеет минимум,
![]() .
.
Литература
1. Фихтенгольц Г.М. Основы математического анализа. Т. 1,
2. М.: Наука, 1968.
2. Шипачев В.С. Задачник по высшей математике. М.: Высшая школа, 2009.
3. Шипачев В.С. Высшая
математика. М.: Юрайт, 2013.
4. Берман Г.Н. Сборник задач по курсу математического
анализа. СПб.: Профессия, 2001.
5. Фихтенгольц Г.М. Курс дифференциального и
интегрального исчисления. Т. 1 –3.
ИД: Лань, 2009.
6. Кудрявцев Л.Д. Курс математического анализа.Т. 1, 2.М.: Высшая школа,
1981.
7. Никольский С.М. Курс
математического анализа.Т.
1, 2. М.: Наука, 1983.
8. Ильин В.А., Позняк Э.Г. Основы математического
анализа. Ч. 1, 2. М.: Наука, 1967.
9. Кудрявцев Л.Д., Кутасов А.Д., Чехлов В.И., Шабунин М.И. Сборник задач по математическому анализу.
Интегралы и ряды. М.: Наука, 1986.
10. Камынин
Л.И. Курс математического анализа.Т.
1, 2. М.: Изд. МГУ, 1995.
11. Архипов Г.И., Садовничий В.А., Чубариков В.Н.
Лекции по математическому анализу.
М., 1999.



