МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ
РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ
ДАГЕСТАНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
АБДУРАГИМОВ Э.И., БЕЙБАЛАЕВ В.Д.
ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ ЗАДАЧИ КОШИ ДЛЯ
ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
Электронный лабораторный практикум
Махачкала 2017
Электронный лабораторный практикум предназначен
для студентов математического факультета специальностей 010100- математика,
010400- прикладная математика и информатика. Оно содержит варианты тем лабораторной
работы и краткие теоретические сведения по теме: «Численные методы решения
дифференциальных уравнений», необходимые для выполнения лабораторной работы по
этой теме. В нем приведен также образец выполнения нулевого варианта
лабораторной работы, аналогичного вариантам, которые должны выполнить студенты.
Студенты математического факультета специальности 010100- математика выполняют
только задание 1, а студенты специальности 010400- прикладная математика и
информатика выполняют задания 1 и 2.
Составители: Абдурагимов Э.И.─доцент кафедры
прикладной математики
ДГУ,
прикладной математики ДГУ
4.
Задание 1
5.
Задание 2
6.
Образец выполнения лабораторной
работы
7. Литература
КРАТКИЕ СВЕДЕНИЯ
Численные методы решения задачи Коши для
обыкновенных дифференциальных уравнений первого порядка
Метод Тейлора. Метод Тейлора является приближенным методом решения задачи Коши. Он
позволяет, зная значения решения и производных решения задачи Коши в некоторой
точке ![]() , найти приближенно решение
, найти приближенно решение ![]() этой задачи в точках
этой задачи в точках ![]() достаточно близких к точке
достаточно близких к точке ![]() .
.
Рассмотрим задачу Коши для
дифференциального уравнения первого порядка
 (1)
(1)
Введем на отрезке ![]() сетку (в общем случае
неравномерную) значений аргумента
сетку (в общем случае
неравномерную) значений аргумента ![]() такую, чтобы
выполнялось соотношение
такую, чтобы
выполнялось соотношение ![]() . Точки
. Точки ![]() называются узлами
сетки. Предполагая, что решение
называются узлами
сетки. Предполагая, что решение ![]() задачи (1) бесконечно
дифференцируема в точке
задачи (1) бесконечно
дифференцируема в точке ![]()
![]() , напишем разложение
, напишем разложение ![]() в окрестности точки
в окрестности точки ![]() :
:
 , (2)
, (2)
где ![]() . Если функция
. Если функция ![]() имеет непрерывные
производные по
имеет непрерывные
производные по ![]() и
и ![]() до порядка
до порядка ![]() , то из (2) получим приближенную формулу
, то из (2) получим приближенную формулу
 . (3)
. (3)
По этой формуле, зная значения ![]() , можно найти приближенно значение
, можно найти приближенно значение ![]() решения задачи Коши
(1) в точке
решения задачи Коши
(1) в точке ![]() близкой к точке
близкой к точке ![]() . Чем ближе точка
. Чем ближе точка ![]() к узлу
к узлу ![]() , тем точнее получим значение решения
, тем точнее получим значение решения ![]() по формуле (3). Если
же значение
по формуле (3). Если
же значение ![]() больше радиуса
сходимости ряда (2), то погрешность не стремится к нулю и предлагаемый метод
неприменим.
больше радиуса
сходимости ряда (2), то погрешность не стремится к нулю и предлагаемый метод
неприменим.
Производные, входящие в правую часть
разложения (3), можно найти, дифференцируя уравнение (1) требуемое число раз.
Например, для первой и второй производных имеем
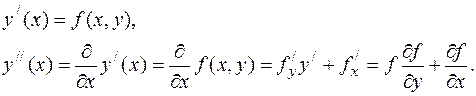
Аналогично
можно найти и производные более высоких порядков.
Однако, использование формулы (3) с
большим значением ![]() имеет ряд недостатков:
во-первых, с ростом порядка производной выражение для нее может оказаться очень
сложным; во-вторых, если функция
имеет ряд недостатков:
во-первых, с ростом порядка производной выражение для нее может оказаться очень
сложным; во-вторых, если функция ![]() известна, лишь
приближенно или задано таблично, ее производные находятся с большой ошибкой. Поэтому
не целесообразно на практике применять формулу (3) с большим значением
известна, лишь
приближенно или задано таблично, ее производные находятся с большой ошибкой. Поэтому
не целесообразно на практике применять формулу (3) с большим значением ![]() .
.
Метод
Эйлера. Метод Эйлера является простейшим численным методом решения задачи
Коши и имеет невысокую точность, поэтому на практике его используют редко.
Однако на его основе легче объяснить алгоритмы более эффективных методов и
способы построения и исследования этих алгоритмов.
Для построения метода Эйлера возьмем в
формуле (3) ![]() и
и ![]() . Получим
. Получим
![]() (4)
(4)
На
основе этого приближенного равенства напишем точное равенство
![]() . (5)
. (5)
Формально
это равенство получается из (4), заменяя ![]() на
на ![]() , приближенное равенство на точное. Если положить
, приближенное равенство на точное. Если положить ![]() при всех
при всех ![]() , то есть шаг интегрирования считать постоянным, то из (5)
получим формулу
, то есть шаг интегрирования считать постоянным, то из (5)
получим формулу
![]() (6)
(6)
которая
называется численным методом Эйлера.
При ![]() , полагая в (6)
, полагая в (6) ![]() , получим
, получим
![]() .
.
Поскольку
правая часть этого равенства известна, то можно найти ![]() . Затем полагая
. Затем полагая ![]() , аналогично находим
, аналогично находим ![]() . Доказывается [1. Бахвалов Н.С., Жидков Н.П., Кобельков Г.М.
Численные методы,
. Доказывается [1. Бахвалов Н.С., Жидков Н.П., Кобельков Г.М.
Численные методы, ![]() непрерывна отрезке
непрерывна отрезке ![]() и имеет непрерывную
производную
и имеет непрерывную
производную ![]() , то
, то
![]() , (7)
, (7)
где
С- постоянная не зависящая от ![]() , т.е. метод Эйлера (6) сходится с первым порядком
сходимости. Поэтому при малом
, т.е. метод Эйлера (6) сходится с первым порядком
сходимости. Поэтому при малом ![]() можно положить
можно положить ![]() .
.
Существует несколько модификаций метода
Эйлера. Например, метод Эйлера- Коши
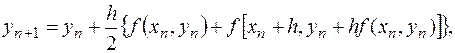
метод Эйлера- Маклорена
 .
.
Обе
эти модификации имеют второй порядок сходимости (см. [1]).
Методы
Рунге-Кутта. Рассмотрим задачу Коши
 (7)
(7)
Рассмотрим одношаговые методы
Рунге-Кутта построения задачи Коши (7). Сначала рассмотрим общий подход к
выводу формул Рунге-Кутта, затем- реализацию этого подхода к построению формул
второго порядка сходимости.
Пусть ![]() три набора чисел,
где
три набора чисел,
где ![]() - некоторое натуральное число. Положим
- некоторое натуральное число. Положим
 (8)
(8)
и
 (9)
(9)
Рассмотрим вопрос о выборе параметров ![]() . Обозначим
. Обозначим ![]() Если
Если ![]() достаточно гладкая функция своих аргументов, то
достаточно гладкая функция своих аргументов, то ![]() и
и ![]() - гладкие функции параметра
- гладкие функции параметра ![]() . Предположим, что
. Предположим, что ![]() настолько гладкая
функция, что существуют производные
настолько гладкая
функция, что существуют производные ![]() , а
, а ![]() выбраны так, что
выбраны так, что
![]() (10)
(10)
Кроме
того, предположим, что существует достаточно гладкая функция ![]() , для которой соответствующее значение
, для которой соответствующее значение ![]() . Согласно формуле Тейлора выполняется равенство
. Согласно формуле Тейлора выполняется равенство
 , (11)
, (11)
где ![]() . Величина
. Величина ![]() называется
погрешностью метода на шаге, а
называется
погрешностью метода на шаге, а ![]() - порядком погрешности метода.
- порядком погрешности метода.
Таким образом, параметры ![]() определяют из системы
(10) при фиксированном
определяют из системы
(10) при фиксированном ![]() . Отметим, что система (10) должна иметь место для
произвольной правой части
. Отметим, что система (10) должна иметь место для
произвольной правой части ![]() уравнения (1).
уравнения (1).
Теперь рассмотрим вывод формул (8), (9) при
значении ![]() . В силу (9) имеем
. В силу (9) имеем
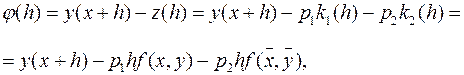
где
![]() . Вычислим производные функции
. Вычислим производные функции ![]() :
:
![]() ,
,
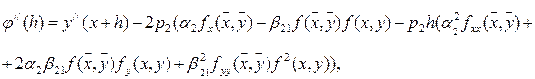
![]()
Согласно исходному дифференциальному
уравнению
![]() .
.
Подставим в выражения ![]() значение
значение ![]() и потребуем выполнение
равенств (10) при всех гладких функциях
и потребуем выполнение
равенств (10) при всех гладких функциях ![]() . Пользуясь последними соотношениями, получим
. Пользуясь последними соотношениями, получим

Соотношение ![]() выполняется при всех
гладких
выполняется при всех
гладких ![]() , если
, если
![]() . (12)
. (12)
Соотношение ![]() выполняется при всех
гладких
выполняется при всех
гладких ![]() , если
, если
![]()
![]() (13)
(13)
Таким
образом, ![]() при всех гладких
при всех гладких ![]() , если выполнены соотношения (12), (13). Задавая произвольно
один из параметров, получим различные методы Рунге-Кутта с погрешностью второго
порядка малости
, если выполнены соотношения (12), (13). Задавая произвольно
один из параметров, получим различные методы Рунге-Кутта с погрешностью второго
порядка малости ![]() .
.
Например, при  получаем
получаем  ,
, ![]() . Тогда в силу (3) имеем
. Тогда в силу (3) имеем
![]()
Этой
приближенной формуле соответствует расчетная формула
 ,
(14)
,
(14)
где ![]() . Формула (14) называется формулой Эйлера-Коши.
. Формула (14) называется формулой Эйлера-Коши.
При ![]() ,
,  в силу (8) получаем
расчетную формулу вида
в силу (8) получаем
расчетную формулу вида
 .
(15)
.
(15)
Формула
(15) называется формулой Эйлера-Маклорена.
В случае уравнения ![]() согласно (11), имеем
согласно (11), имеем ![]() независимо от значений
независимо от значений
![]() . Отсюда следует, что нельзя построить формулы Рунге-Кутта со
значениями
. Отсюда следует, что нельзя построить формулы Рунге-Кутта со
значениями ![]() и
и ![]() .
.
Для погрешности метода на шаге в силу
(11) получим выражение
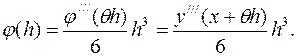
Во многих пакетах прикладных программ
используются следующие формулы Рунге-Кутта третьего порядка точности
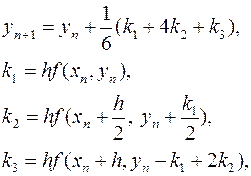
и
четвертого порядка точности

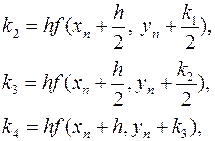
которые
можно построить указанным методом.
· Экстраполяционный метод Адамса
· Интерполяционный метод Адамса
Экстраполяционный метод Адамса. Рассмотрим задачу Коши
 (16)
(16)
Пусть,
каким либо образом найдены значения ![]() и требуется найти
приближенное решение задачи (16) в следующих точках
и требуется найти
приближенное решение задачи (16) в следующих точках ![]() ,
,  . Приближенные значения решения задачи
. Приближенные значения решения задачи ![]() , могут быть вычислены методом Рунге-Кутта либо Эйлера.
Начало решения должно быть вычислено с большей точностью. Если для нахождения
начала решения применяется метод Рунге-Кутта, то величина шага
, могут быть вычислены методом Рунге-Кутта либо Эйлера.
Начало решения должно быть вычислено с большей точностью. Если для нахождения
начала решения применяется метод Рунге-Кутта, то величина шага ![]() для него нужно брать
меньшую, чем для последующей схемы расчета.
для него нужно брать
меньшую, чем для последующей схемы расчета.
Расчетное правило экстраполяционного
метода Адамса имеет вид
 , (17)
, (17)
где
![]()
![]() - конечные разности
- конечные разности ![]() -го порядка,
-го порядка,
 .
.
Для
остаточного члена имеет место следующая оценка:
![]()
где
![]() .
.
В экстраполяционном методе Адамса
убывание абсолютных величин слагаемых происходит главным образом за счет
убывания абсолютных величин конечных разностей. Этим в основном и
руководствуются, выбирая ![]() и
и ![]() : чем меньше возьмем шаг
: чем меньше возьмем шаг ![]() , тем ниже при постоянных требованиях к точности будет
порядок
, тем ниже при постоянных требованиях к точности будет
порядок ![]() последней участвующей
в вычислениях конечной разности и тем меньше слагаемых будет содержать правая
часть формулы (17). Однако, уменьшив шаг, мы тем самым увеличиваем число
узловых точек на данном отрезке, что дает возможность применять укороченную
формулу большое число раз, а это, как правило, сопряжено с ростом погрешности.
Обычно
последней участвующей
в вычислениях конечной разности и тем меньше слагаемых будет содержать правая
часть формулы (17). Однако, уменьшив шаг, мы тем самым увеличиваем число
узловых точек на данном отрезке, что дает возможность применять укороченную
формулу большое число раз, а это, как правило, сопряжено с ростом погрешности.
Обычно ![]() и
и ![]() стараются подобрать
так, чтобы последняя конечная разность, участвующая в вычислениях, была
практически постоянной в пределах принятой точности. Например, если третья конечная
разность в пределах принятой точности практически постоянна, то правило (17)
примет вид
стараются подобрать
так, чтобы последняя конечная разность, участвующая в вычислениях, была
практически постоянной в пределах принятой точности. Например, если третья конечная
разность в пределах принятой точности практически постоянна, то правило (17)
примет вид
 (18)
(18)
с
локальной ошибкой дискретизации
 .
.
Таким
образом, метод Адамса (18) имеет четвертый порядок точности на интервале. Чтобы
начать счет по схеме Адамса, необходимо знать решение в четырех начальных
точках ![]() .
.
Интерполяционный метод Адамса. Рассмотрим интерполяционную формулу
Адамса вида:
![]() (19)
(19)
где ![]()
 .
.
Для
остаточного члена имеет место следующая оценка:
![]()
где
![]() .
.
Использование вычислительной схемы
интерполяционного метода Адамса связано со следующей особенностью. Так как в
равенстве (19) величина ![]() входит в правую часть,
начиная со второго члена, то имеем уравнение для нахождения этой величины. В
практике используют обычно такой прием: по формулам (17) экстраполяционного
метода Адамса вычисляют
входит в правую часть,
начиная со второго члена, то имеем уравнение для нахождения этой величины. В
практике используют обычно такой прием: по формулам (17) экстраполяционного
метода Адамса вычисляют ![]() , затем это значение применяют в правой части формулы (19)
для нахождения
, затем это значение применяют в правой части формулы (19)
для нахождения ![]() «коррекционного»
значения. Затем это коррекционное значение можно снова уточнить по формуле
(19), пока не добьются требуемой точности.
«коррекционного»
значения. Затем это коррекционное значение можно снова уточнить по формуле
(19), пока не добьются требуемой точности.
Одношаговая:
![]()
Двухшаговая: ![]()
Трехшаговая: ![]()
Четырехшаговая: ![]()
II.
Интерполяционные(неявные) формулы
Одношаговая: ![]()
Двухшаговая: ![]()
Трехшаговая: ![]()
Четырехшаговая:
![]()
![]() Перейти к содержанию темы
Перейти к содержанию темы
· Варианты
· План отчета по лабораторной работе
Найти приближенное решение
задачи Коши на отрезке ![]() для данного
дифференциального уравнения (пункт а) варианта ) с заданными начальными условиями
указанным в варианте одношаговым методом с точностью
для данного
дифференциального уравнения (пункт а) варианта ) с заданными начальными условиями
указанным в варианте одношаговым методом с точностью ![]() . Для этого составить алгоритм, выбрать
. Для этого составить алгоритм, выбрать ![]() шаг метода и составить соответствующую программу решения
задачи на ЭВМ. Для контроля работы составленной программы сначала по этой
программе найти приближенное решение задачи Коши пункта б) на том же отрезке
шаг метода и составить соответствующую программу решения
задачи на ЭВМ. Для контроля работы составленной программы сначала по этой
программе найти приближенное решение задачи Коши пункта б) на том же отрезке ![]() ( тестовая задача
); проверить верно ли оно найдено,
находя точное решение этой задачи
( тестовая задача
); проверить верно ли оно найдено,
находя точное решение этой задачи ![]() . Шаг метода
. Шаг метода ![]() выбрать так, чтобы
выбрать так, чтобы ![]() где
где ![]() порядок метода. Например, для метода Эйлера-Коши
порядок метода. Например, для метода Эйлера-Коши ![]() поэтому
поэтому ![]() выбираем так, чтобы
выбираем так, чтобы ![]() Можно взять
Можно взять ![]()
Выписать значения полученного решения в точках  - шаг таблицы. Заполнить таблицу вида
- шаг таблицы. Заполнить таблицу вида
Таблица результатов
![]()
![]()
|
|
0.0 |
0.2 |
0.4 |
. . . |
2.0 |
||
|
б) |
|||||||
|
|
|
|
|
. . . |
|
||
|
|
|
|
|
. . . |
|
||
|
|
|||||||
|
а) |
|||||||
|
|
|
|
|
. . . |
|
||
При заполнении таблицы в результатах
для ![]() и
и ![]() сохранять по два
десятичных знака. Значение
сохранять по два
десятичных знака. Значение ![]() выписать с плавающей
точкой с двумя значащими цифрами (например,
выписать с плавающей
точкой с двумя значащими цифрами (например, ![]() ). По данным таблицы построить график решения задачи Коши
пункта а) варианта. Сделать выводы о
поведении решения.
). По данным таблицы построить график решения задачи Коши
пункта а) варианта. Сделать выводы о
поведении решения.
|
№ пп |
Дифференциальное уравнение |
Начальные условия |
Отрезок [a,b] |
Численный метод |
|
1 |
|
|
[0; 2] |
Рунге-Кутта 4-го порядка точности |
|
2 |
|
|
[1; 2] |
Эйлера-Коши |
|
3 |
|
|
[1;2,6] |
Рунге- Кутта 3-го порядка |
|
4 |
|
|
[0; 1] |
Эйлера-Маклорена |
|
5 |
|
|
[0; 1] |
Рунге-Кутта 4-го порядка
точности |
|
6 |
|
|
[1; 2,4] |
Эйлера-Маклорена |
|
7 |
|
|
[1; 2] |
Эйлера-Коши Рунге-Кутта 3-го
порядка точности |
|
8 |
|
|
[0; 2] |
Эйлера-Маклорена |
|
9 |
|
|
[0; 1] |
Эйлера-Коши |
|
10 |
|
|
[0; 2,8] |
Рунге-Кутта 3-го порядка
точности |
|
11 |
|
|
[0; 1,2] |
Эйлера-Коши |
|
12 |
|
|
[0; 2] |
Рунге-Кутта 3-го порядка
точности |
|
13 |
|
|
|
Эйлера-Маклорена |
|
14 |
|
|
[0;0,8] |
Эйлера-Коши |
|
15 |
|
|
[0; 1,2] |
Рунге-Кутта 4-го порядка
точности |
|
16 |
|
|
[0, 1] |
Эйлера-Маклорена |
|
17 |
|
|
[0; 1,2] |
Эйлера-Коши |
|
18 |
|
|
[0; 2] |
Рунге-Кутта 4-го порядка
точности |
|
19 |
|
|
[0; 2] |
Рунге-Кутта 3-го порядка
точности |
|
20 |
|
|
[0; 2,4] |
Эйлера-Коши |
|
21 |
|
|
[0; 2] |
Рунге-Кутта 4-го порядка
точности |
|
22 |
|
|
[0; 1] |
Эйлера-Маклорена |
|
23 |
|
|
[0; 2,8] |
Эйлера-Коши |
|
24 |
|
|
[1; 2,4] |
Рунге-Кутта 3-го порядка
точности |
|
25 |
|
|
[0; 2] |
Эйлера-Маклорена |
Отчет по
заданию 1 работы должен содержать
2.
Схема алгоритма решения
задачи.
3.
Программа на ЭВМ, составленная по схеме алгоритма.
4.
Таблица результатов вида указанного в задании.
5.
График решения задачи Коши ( пункт а) варианта).
6.Выводы
относительно поведения решения задачи Коши ( пункт а) варианта) на отрезке ![]() .
.
· Варианты
· План отчета по лабораторной работе
Решить задачу Коши указанным методом на
отрезке [0;a] для данных значений параметра
А. Шаг интегрирования взять равным h.
Решение задачи Коши получить для указанных значений параметра A в данных точках
xi из отрезка [0;a]. Приближённые значения yi решения в точках xi, полученные явным k-шаговым методом Адамса, каждый раз уточнять неявным
k-шаговым методом Адамса. Необходимые для начала вычислений по k-шаговым формулам Адамса k начальных значений ![]() вычислить каким-либо одношаговым методом
Рунге-Кутта. Составить таблицы вида:
вычислить каким-либо одношаговым методом
Рунге-Кутта. Составить таблицы вида:
А=0
|
xi |
0 |
0.1 |
0.2 |
… |
1.0 |
|
y(xi) |
0 |
0.1263 |
0.2947 |
… |
3.2678 |
A=1
|
xi |
0 |
0.1 |
0.2 |
… |
1.0 |
|
y(xi) |
0 |
0.2015 |
0.4163 |
… |
4.8762 |
и т.д.
По данным этих таблиц построить
графики решений для двух каких─либо значений параметра A. Сделать выводы относительно зависимости решения от значений параметра A.
|
№ п/п |
Задача Коши |
Шаг h |
Отрезок [0;a] |
Метод |
Точки, в которых необходи-мо
найти решение |
Значения пара- метра A |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
1. |
|
0.01 |
[0;1] |
Двухшаговый метод Адамса (q=1) |
|
A=0,
|
|
2. |
|
0.01 |
[0;1] |
Трёхшаговый метод Адамса (q=2) |
|
A=0,1,2, 3,4 |
|
3. |
|
0.05 |
[0;1] |
Четырехшаго- вый метод Адамса (q=3) |
|
|
|
4 |
|
0.01 |
[0;0.4] |
Четырехшаго- вый метод Адамса (q=3) |
|
A=-2,
-1,0,1,2
|
|
5 |
|
0.01 |
[0;0.5] |
Четырехшаго вый метод Адамса (q=3) |
|
A=-2, -1,0,1,2 |
|
6 |
|
0.01 |
[0;1] |
Двухшаговый метод Адамса (q=1) |
|
A=1,2,3,4
|
|
7 |
|
0.01 |
[0;2] |
Трёхшаговый метод Адамса (q=2) |
|
A=0,1,-2 |
|
8 |
|
0.05 |
[0;1] |
Четырехшаго- вый метод Адамса (q=3) |
|
A=0,1,2,4 |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
9 |
|
0.01 |
[0;0.5] |
Четырехшаго- вый метод Адамса (q=3) |
|
A=0,1,2,4 |
|
10 |
|
0.01 |
[0;0.5] |
Трёхшаговый метод Адамса (q=2) |
|
A=0,1,2 |
|
11 |
|
0.1 |
[0;2] |
Двухшаговый метод Адамса (q=1) |
|
A=1,2, 4,5 |
|
12 |
|
0.01 |
[0;2] |
Трёхшаговый метод Адамса (q=2) |
|
|
|
13 |
|
0.01 |
[0;1] |
Двухшаговый метод Адамса (q=1) |
|
A=0,1,2,3 |
|
14 |
|
0.01 |
[0;1] |
Четырехшаго- вый метод Адамса (q=3) |
|
|
|
15 |
|
0.01 |
[0;0.5] |
Двухшаговый метод Адамса (q=1) |
|
|
|
16 |
|
0.01 |
[0;1] |
Трёхшаговый метод Адамса (q=2) |
|
A=0,1,2,5 |
|
17 |
|
0.01 |
[0;1] |
Четырехшаго- вый метод Адамса (q=3) |
|
A=0,2,5 |
Отчет по
заданию 2 работы должен содержать
2.
Схема алгоритма решения задачи.
3.
Программа на ЭВМ, составленная по схеме алгоритма.
4.
Таблица результатов вида указанного в задании.
5.
Графики решений для каких либо двух значений параметра А.
6.Выводы
о зависимости решения от параметра А.
ОБРАЗЕЦ
ВЫПОЛНЕНИЯ ЛАБОРАТОРНОЙ РАБОТЫ
Вариант 0
Задание 1
Найти решение задачи Коши
 (0.1)
(0.1)
одношаговым
методом Рунге-Кутта 4-го порядка точности.
Обозначая в уравнении ![]() , перейдем к задаче Коши для системы дифференциальных
уравнений
, перейдем к задаче Коши для системы дифференциальных
уравнений
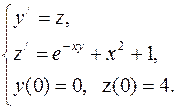
Эту
задачу можно записать в векторной форме следующим образом
 (0.2)
(0.2)
где
 ,
,
![]() .
.
Пусть известно значение вектора  в точке
в точке ![]() ( в нашем случае это
( в нашем случае это ![]() и
и ![]() ). Укажем схему алгоритма, по которому пользуясь формулами
(0.3), (0.4) можно найти следующую точку
). Укажем схему алгоритма, по которому пользуясь формулами
(0.3), (0.4) можно найти следующую точку
![]() и приближенное
значение вектора
и приближенное
значение вектора ![]() (в нашем случае
(в нашем случае ![]() ).
).
1. Вводим ![]() - число уравнений в системе (в нашем случае их два, поэтому
- число уравнений в системе (в нашем случае их два, поэтому ![]() ),
), ![]() - шаг,
- шаг, ![]() - точность.
- точность.
2.
Задаем правую
часть системы в виде некоторой процедуры pr, в которой
![]()
3.
Считая ![]() и вектор
и вектор ![]() известным (например, известны начальные данные
известным (например, известны начальные данные ![]() ), вычисляем с помощью процедуры pr правую часть системы при этих значениях
), вычисляем с помощью процедуры pr правую часть системы при этих значениях ![]() и
и ![]() . С ее помощью вычисляем вектор
. С ее помощью вычисляем вектор ![]() :
: ![]() , затем вычисляем
, затем вычисляем ![]() и вектор
и вектор 
![]() и соответствующую им
правую часть
и соответствующую им
правую часть ![]() с помощью процедуры pr. Тогда
с помощью процедуры pr. Тогда ![]() .
.
4.
Затем вычисляем вектор 
![]() . По значениям
. По значениям ![]() и
и  с помощью процедуры pr вычисляем правую часть
с помощью процедуры pr вычисляем правую часть ![]() . Тогда
. Тогда ![]() . Затем вычисляем аргумент
. Затем вычисляем аргумент ![]() и аргумент
и аргумент ![]()
![]() . По этим данным с помощью процедуры pr вычисляем правую часть
. По этим данным с помощью процедуры pr вычисляем правую часть ![]() . Тогда
. Тогда ![]() . Наконец, вычисляем вектор
. Наконец, вычисляем вектор  . Это и будет приближенным значением решения в точке
. Это и будет приближенным значением решения в точке ![]() , т.е.
, т.е. ![]() .
.
По
указанной схеме можно составить процедуру (на языке Паскаль) в которой по
входным данным ![]() вычисляются выходные данные
вычисляются выходные данные ![]() - следующие значения. Далее, считая
- следующие значения. Далее, считая ![]() входными данными можно
по этой процедуре вычислить следующие значения
входными данными можно
по этой процедуре вычислить следующие значения ![]() и т.д. Таким образом,
обращаясь к этой процедуре в цикле можно найти приближенное решение в
точках
и т.д. Таким образом,
обращаясь к этой процедуре в цикле можно найти приближенное решение в
точках ![]() . В нашем случае сначала задаем начальные данные
. В нашем случае сначала задаем начальные данные ![]() :
:
![]() .
(0.3)
.
(0.3)
Затем обращаясь к процедуре ![]() , составленную по вышеуказанному алгоритму, в ней по входным
данным (0.3) будут вычислены выходные данные
, составленную по вышеуказанному алгоритму, в ней по входным
данным (0.3) будут вычислены выходные данные ![]() . Если теперь еще раз обратится к процедуре
. Если теперь еще раз обратится к процедуре ![]() , считая полученные выходные данные
, считая полученные выходные данные ![]() за входные данные,
будут вычислены выходные данные
за входные данные,
будут вычислены выходные данные ![]() т.е
т.е ![]() . Таким образом, задав входные данные (0.3) и обращаясь
в цикле
. Таким образом, задав входные данные (0.3) и обращаясь
в цикле ![]() к процедуре
к процедуре
![]() получим
последовательность
получим
последовательность ![]()
![]() - значений узлов
- значений узлов ![]() , приближенных значений
решения
, приближенных значений
решения ![]() и приближенные значения производных решения
и приближенные значения производных решения ![]() . При каждом значении
. При каждом значении ![]() их можно распечатать. В результате получим
таблицу значений решения
их можно распечатать. В результате получим
таблицу значений решения ![]() (производные
(производные ![]() можно не распечатывать, если нет необходимости
их распечатывать).
можно не распечатывать, если нет необходимости
их распечатывать).
Аналогично составляются схемы алгоритма и
для методов Рунге-Кутта второго порядка (Эйлера-Коши, Эйлера-Маклорена) и
третьего порядка.
Приводим
программу на языке Паскаль для этих методов, составленную в соответствии с
приведенной здесь схеме алгоритма. В нашем случае требуется решить данную
задачу методом Рунге-Кутта 4-го порядка точности. Поэтому в головной программе,
задав ![]() , обращаемся к процедуре
, обращаемся к процедуре ![]() из описанных в
программе процедур.
из описанных в
программе процедур.
Работу
составленной программы предварительно проверяем на аналогичной тестовой задаче:
![]()
с решением ![]() . Убедившись, что верно (с
применяемой точностью) решена тестовая задача, по этой же программе, внося в
нее соответствующие изменения, решаем задачу Коши своего варианта.
. Убедившись, что верно (с
применяемой точностью) решена тестовая задача, по этой же программе, внося в
нее соответствующие изменения, решаем задачу Коши своего варианта.
Задание 2
Найти решение задачи Коши
 (0.4)
(0.4)
четырехшаговым
методом Адамса с шагом ![]() при значениях параметра
при значениях параметра ![]()
Решения задачи Коши для обыкновенного
дифференциального уравнения
ses crt; {$F+}
const
n=2;
type
vect = array [1..n] of real;
prc = procedure (x:real; y:vect; var
f:vect);
Var
y,u,f,f0,f1,f2,f3,f4,fn,fn1,fn2,fn3,fnp:vect;
i,j,k:integer;
h,x,x0:real;
{-----------------------------------------------------------}
procedure pr1(x:real; y:vect; var f:vect);
Begin
f[1]:=y[2];
f[2]:=3*y[2]-2*y[1]+2*x-3;
end;
procedure rgkem(var x:real; h:real; var y:vect; pr:prc);
var
i:integer;
k1,k2,k3,k4:vect;
Begin
u:=y;
pr(x,y,f);
for i:=1 to n do k1[i]:=h*f[i] ;
x:=x+h/2;
for i:=1 to n do
y[i]:=u[i]+k1[i]/2;
pr(x,y,f);
for i:=1 to n do k2[i]:=h*f[i] ;
for i:=1 to n do
y[i]:=u[i]+k2[i]; x:=x+h/2;
end;
procedure rgkek(var x:real; h:real; var y:vect; pr:prc);
var
i:integer;
k1,k2,k3,k4:Vect;
Begin
u:=y;
pr(x,y,f);
for i:=1 to n do k1[i]:=h*f[i] ;
x:=x+h;
for i:=1 to n do
y[i]:=u[i]+k1[i];
pr(x,y,f);
for i:=1 to n do k2[i]:=h*f[i] ;
for i:=1 to n do
y[i]:=u[i]+(k1[i]+k2[i])/2;
end;
procedure rgk3(var x:real; h:real; var y:vect; pr:prc);
var
i:integer;
k1,k2,k3,k4:Vect;
Begin
u:=y;
pr(x,y,f);
for i:=1 to n do k1[i]:=h*f[i] ;
x:=x+h/2;
for i:=1 to n do
y[i]:=u[i]+k1[i]/2;
pr(x,y,f);
for i:=1 to n do k2[i]:=h*f[i];
x:=x+h/2;
for i:=1 to n do
y[i]:=u[i]-k1[i]+2*k2[i];
pr(x,y,f);
for i:=1 to n do k3[i]:=h*f[i];
y[i]:=u[i]+(k1[i]+4*k2[i]+k3[i])/6;
end;
procedure rgk4(var x:real; h:real; var y:vect; pr:prc);
var
i:integer;
k1,k2,k3,k4:Vect;
Begin
u:=y;
pr(x,y,f);
for i:=1 to n do k1[i]:=h*f[i] ;
x:=x+h/2;
for i:=1 to n do
y[i]:=u[i]+k1[i]/2;
pr(x,y,f);
for i:=1 to n do k2[i]:=h*f[i];
for i:=1 to n do
y[i]:=u[i]+k2[i]/2;
pr(x,y,f);
for i:=1 to n do k3[i]:=h*f[i] ;
x:=x+h/2;
for i:=1 to n do
y[i]:=u[i]+k3[i];
pr(x,y,f);
for i:=1 to n do k4[i]:=h*f[i];
for i:=1 to n do
y[i]:=u[i]+(k1[i]+2*(k2[i]+k3[i])+k4[i])/6;
end;
procedure adext2(var x:real;
h:real; fn, fn1:vect; var y:vect; pr:prc);
begin
u:=y;
for i:=1 to n do
y[i]:=u[i]+h/2*(3*fn[i]-fn1[i]); x:=x+h;
end;
procedure adext3(var x:real;
h:real; fn, fn1,fn2:vect; var y:vect; pr:prc);
begin
u:=y;
for i:=1 to n do
y[i]:=u[i]+h/12*(23*fn[i]-16*fn1[i]+5*fn2[i]); x:=x+h;
end;
procedure adext4(var x:real;
h:real; fn, fn1,fn2,fn3:vect; var y:vect; pr:prc);
begin
u:=y;
for i:=1 to n do
y[i]:=u[i]+h/24*(55*fn[i]-59*fn1[i]+37*fn2[i]-9*fn3[i]);
x:=x+h
end;
procedure adint2(x:real;
h:real;fnp, fn,fn1:vect; y:vect;
pr:prc);
begin
u:=y;
for i:=1 to n do
y[i]:=u[i]+h/12*(5*fnp[i]+8*fn[i]-fn1[i]);
end;
procedure adint3(x:real;
h:real; fnp, fn,fn1,fn2:vect; y:vect; pr:prc);
begin
u:=y;
for i:=1 to n do
y[i]:=u[i]+h/24*(9*fnp[i]+19*fn[i]-5*fn1[i]+fn2[i]);
end;
procedure adint4(x:real; h:real;
fnp, fn,fn1,fn2,fn3:vect; y:vect; pr:prc);
begin
u:=y;
for i:=1 to n do
y[i]:=u[i]+h/720*(251*fnp[i]+646*fn[i]-
264*fn1[i]+106*fn2[i]-19*fn3[i]);
end;
{-----------------------------------------------------------}
begin
clrscr;
x:=0; y[1]:=0; y[2]:=4;
h:=0.1;
{ writeln;
writeln('vtoroi poryadok');
writeln('x= ',x:3:1,' y=',y[1]:6:3,' yt=', 3*(exp(2*x-exp(x))+x:6:3);
for k:=1 to 20 do
begin
rgkem(x,h,y,pr1);
if k=19 then pr1(x,y,fn1);
if k=20 then pr1(x,y,fn);
if k mod 1=0 then
writeln('x= ',x:4:2,' y=',y[1]:6:3,' yt=',3*(exp(2*x-exp(x))+x:6:3);
end;
readkey;
for k:=1 to 100 do
begin
adext2(x,h,fn,fn1,y,pr1);
pr1(x,y,fnp);
if k mod 10=0 then
writeln('xe=',x:4:2,' y=',y[1]:6:3,' yt=', 3*(exp(2*x-exp(x))+x:6:3);
adint2(x,h,fnp,fn,fn1,y,pr1);
if k mod 10=0 then
writeln('xi=',x:4:2,' y=',y[1]:6:3,' yt=', 3*(exp(2*x-exp(x))+x:6:3);
fn1:=fn;fn:=fnp;
end;
readkey;
writeln('tretii poryadok');
x:=0; y[1]:=0; y[2]:=1;
writeln('x= ',x:4:2,' y=',y[1]:6:3,' yt=', 3*(exp(2*x-exp(x))+x:6:3);
for k:=1 to 100 do
begin
rgk3(x,h,y,pr1);
if k=98 then pr1(x,y,fn2);
if k=99 then pr1(x,y,fn1);
if k=100 then pr1(x,y,fn);
if k mod 10=0 then
writeln('x= ',x:4:2,' y=',y[1]:6:3,' yt=', 3*(exp(2*x-exp(x))+x:6:3);
end;
readkey;
for k:=1 to 100 do
begin
adext3(x,h,fn,fn1,fn2,y,pr1);
pr1(x,y,fnp);
if k mod 10=0 then
writeln('xe=',x:4:2,' y=',y[1]:6:3,' yt=', 3*(exp(2*x-exp(x))+x:6:3);
adint3(x,h,fnp,fn,fn1,fn2,
y,pr1);
if k mod 10=0 then
writeln('xi=',x:4:2,' y=',y[1]:6:3,' yt=', 3*(exp(2*x-exp(x))+x:6:3);
fn2:=fn1; fn1:=fn; fn:=fnp;
end;
readkey;}
writeln;
writeln('chetvertii
poryadok'); h:=0.1;
x:=0; y[1]:=0; y[2]:=4;
writeln('x= ',x:4:2,' y=',y[1]:6:3,' yt=', 3*(exp(2*x-exp(x))+x:6:3);
for k:=1 to 20 do
begin
rgk4(x,h,y,pr1);
if k=17 then pr1(x,y,fn3);
if k=18 then pr1(x,y,fn2);
if k=19 then pr1(x,y,fn1);
if k=20 then pr1(x,y,fn);
if k mod 1=0 then
writeln('x= ',x:4:2,' y=',y[1]:6:3,' yt=', 3*(exp(2*x-exp(x))+x:6:3);
end;
readkey;
for k:=1 to 10 do
begin
adext4(x,h,fn,fn1,fn2,fn3,y,pr1); pr1(x,y,fnp);
if k mod 1=0 then
writeln('xe=',x:4:2,' y=',y[1]:6:3,' yt=', 3*(exp(2*x-exp(x))+x:6:3);
adint4(x,h,fnp,fn,fn1,fn2,fn3, y,pr1);
if k mod 1=0 then
writeln('xi=',x:4:2,' y=',y[1]:6:3,' yt=', 3*(exp(2*x-exp(x))+x:6:3);
fn3:=fn2; fn2:=fn1;fn1:=fn;
fn:=fnp;
end;
readkey;
end.
|
|
0.0 |
0.2 |
0.4 |
0.6 |
0.8 |
1.0 |
1.2 |
1.4 |
1.6 |
1.8 |
2.0 |
|
б) |
|||||||||||
|
|
0.00 |
1.01 |
2.60 |
5.09 |
8.98 |
15.01 |
24.31 |
38.57 |
60.34 |
93.44 |
144.62 |
|
|
0.00 |
1.011 |
2.60 |
5.09 |
8.98 |
15.01 |
24.31 |
38.57 |
60.34 |
93.45 |
143.63 |
|
|
|||||||||||
|
а) |
|||||||||||
|
|
0.00 |
0.84 |
1.75 |
2.74 |
3.78 |
4.89 |
6.09 |
7.38 |
8.79 |
10.34 |
12.06 |
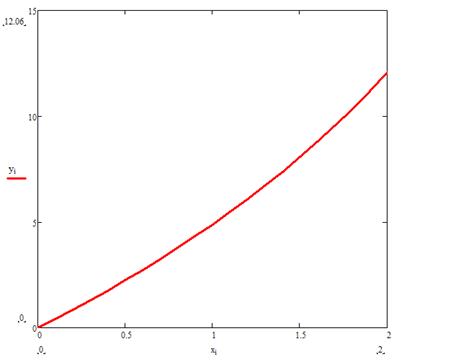
Рис. 1. График решения ![]() задачи (0.1)
задачи (0.1)
|
|
0.00 |
0.10 |
0.20 |
0.30 |
0.40 |
|
|
0.000 |
0.405 |
0.816 |
1.224 |
1.613 |
![]()
|
|
0.00 |
0.10 |
0.20 |
0.30 |
0.40 |
|
|
0.000 |
0.400 |
0.798 |
1.190 |
1.568 |
![]()
|
|
0.00 |
0.10 |
0.20 |
0.30 |
0.40 |
|
|
0.000 |
0.395 |
0.780 |
1.155 |
1.520 |
![]()
|
|
0.00 |
0.10 |
0.20 |
0.30 |
0.40 |
|
|
0.000 |
0.390 |
0.762 |
1.119 |
1.468 |
![]()
|
|
0.00 |
0.10 |
0.20 |
0.30 |
0.40 |
|
|
0.000 |
0.385 |
0.744 |
1.083 |
1.414 |
|
|
|
|
|
|
|
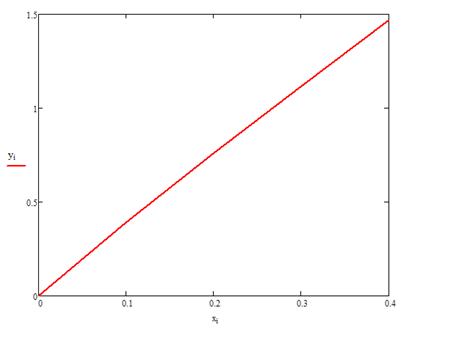
Рис. 2.
График решения задачи (0.4) при ![]() .
.
ЛИТЕРАТУРА
1. В.И. Крылов, В.В. Бобков, П.И. Монастырный.
Вычислительные методы, т.2. -М.: Наука, 1977.-400 с.
2. Н.С. Бахвалов, Н.П. Жидков, Г.М. Кобельков. Численные
методы. -М.: Наука, 1987. - 600 с.

























