§ 5. Спектральное представление стационарных случайных процессов с дискретным спектром

Рассмотрим случайный процесс вида

(1)

где -постоянное число, а и -центрированные некоррелированные случайные величины, причем .

Понятно, что и случайный процесс (1) может быть представлен в виде

(2)

где

Как видно из (2), случайный процесс (1) задает гармонические колебания со случайной амплитудой

И случайной фазой , частотой колебаний . Легко убедится в том, что

(3)

Дисперсия процесса задается одним числом, каноническое разложение (1)- единственным значением . Поэтому процесс (1) называют тривиальным стационарным процессом с дискретным спектром.

Теперь рассмотрим обобщение процесса (1), а именно действительный случайный процесс вида

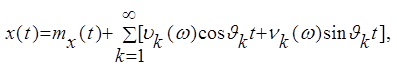(4)

где , -центрированные попарно некоррелированные случайные величины с конечными дисперсиями

Представление (4) называется спектральным представлением, разложением случайного процесса.

Оно же является и каноническим разложением действительного случайного процесса с дискретным спектром. Ясно, что

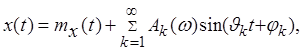(5)

где ,

Нетрудно убедиться, что ковариационная функция

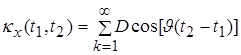, (6)

и, соответственно дисперсия

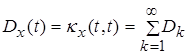. (7)

Дисперсия стационарного случайного процесса , представленного спектральным разложением (4), равна сумме дисперсий всех гармоник его разложения. Совокупность дисперсий всех составляющих процесс гармоник называется его дискретным спектром. Соответственно значения , обычно называют частотами, в совокупности образуют частотный спектр стационарного процесса.

При известном спектральном разложении (4) мы имеем спектральное разложение ковариационной функции (6), записываемое в следующей эквивалентной форме

, (8)

а также представление (7) для дисперсии. Возникает вопрос как получить разложение (4) при известной ковариационной функции ?

Вполне понятно, что коэффициенты в разложении (8) и набор различных частот должны зависеть от свойств, конкретного вида ковариационной функции . Но в то же время эту зависимость можно получить различными способами, разлагая ковариационную функцию в ряд.

Функция четная и его можно разложить в ряд Фурье по косинусам на интервале (-Т,Т).

Выберем частоты и , k=0,1,2,…

тогда ряд Фурье для будет иметь вид

(9)

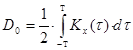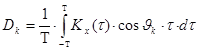где , (10)

Следует отметить это можно доказать для любой ковариационной функции стационарного случайного процесса коэффициенты , k=0,1,2,… будут неотрицательными величинами. По частотам и дисперсиям подбираются случайные величины и . Полученное разложение (9) тем точнее, чем больше интервал разложения. При этом сумма коэффициентов любого разложения (9) одна и та же она равна дисперсии процесса .

В комплексной форме спектральным разложением случайного процесса с дискретным спектром называется представление вида

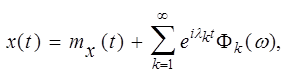(11)

где -центрированные попарно некоррелированные случайные величины, -некоторые действительные числа, .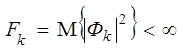

Спектральное разложение ковариационной функции соответственно принимает вид

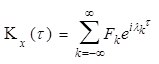. (12)

Задача 1. Случайный процесс задан уравнением 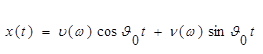,-центрированные некоррелированные случайные процессы, -некоторая константа, Найти спектральную плотность

Решение. x(t) представляет собой простейший случайный процесс с дискретным спектром сосредоточенный в одной точке. Как нетрудно убедиться, его ковариационная функция зависит лишь от разности аргументов, причем

.

Если масса сосредоточена в конкретной точке трехмерного пространства, то плотность этой массы задается выражением

,

где - дельта функция Дирака. Аналогично задаются распределения разных физических величин, сосредоточенных по точечно.

Спектр случайного процесса распределен на вещественной оси, а нашем примере в конкретной точке .

Поэтому естественно ожидать что спектральная плотность имеет вид

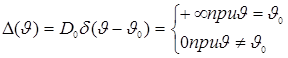, (13)

Причем

Покажем, что данная функция действительно является спектральной плотностью. Иными словами, требуется уточнить, что

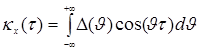. (14)

Подставив выражение для в последнюю формулу, имеем в соответствии со свойствами -функций, что

.

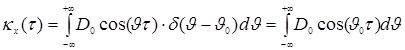Функции и связки друг с другом преобразованием Фурье F:

.

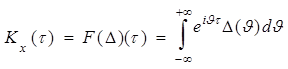Поскольку преобразование Фурье является взаимно-однозначным отображением, то функция , удовлетворяющий равенству (14), единственна, то есть функция (13) действительно является спектральной плотностью исходного процесса.

Задача 2. Действительный стационарный случайный процесс задан своим спектральным разложением

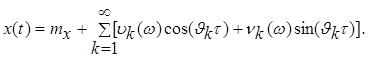
Определить спектральную плотность процесса.

Решение. Ковариационная функция процесса имеет вид

,

Спектральная плотность есть интервальные преобразование ковариационной функции:

,

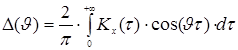т.е.

Но поскольку согласно предыдущей задаче

,

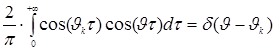то мы приходим к равенству

.