§4. Спектральное разложение ковариационной функции действительного спектрального стационарного случайного процесса с непрерывным спектром

В случае вещественного стационарного случайного процесса ковариационная функция четная и потому формула (9) спектральной плотности принимает вид

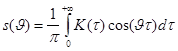(1)

Как видно из полученного соотношения (1), в этом случае и спектральная плотность четная и ковариационной функции получим представление

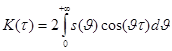(2)

Поскольку в случае стационарных процессов то

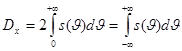(3)

Полезными характеристиками стационарных случайных процессов с непрерывным спектром являются эффективная ширина спектра и эффективная длительность корреляции , средний интервал корреляции, определяемые следующими формулами:

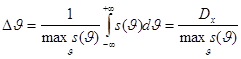(4)

(5)

Эффективная ширина спектра равна длине основания прямоугольника с высотой , площадь которого равна площади под кривой . Точно также эффективная длительность корреляции рана длине основания прямоугольника с высотой , площадь которого равна площади под кривой .

Из приведенных определений и формулы (5) вытекает, что величина связаны между собой соотношением

(6)

обычно называемым «соотношением неопределенности».

Смысл соотношения неопределенности состоит в следующем: чем уже ширина спектра стационарного процесса, тем больше интервал корреляции его сечений, и наоборот.

Спектральная плотность производной процесса связана с плотностью самого процесса соотношением

Для того чтобы стационарный случайный процесс x(t) был дифференцируемым, необходимо и достаточно выполнение условия,

Задача 1. Ковариационная функция стационарного случайного процесса x(t) задана в виде

Найти спектральную плотность и эффективные характеристики

Решение. Согласно формуле (8) имеем:

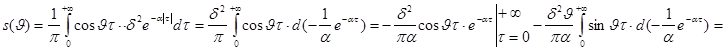
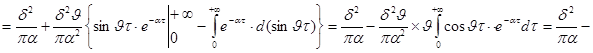
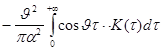
Итак, мы пришли к уравнению

откуда

Спектральную плотность можно вычислить и согласно формула (6):

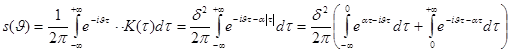
Проведя формальное интегрирование комплекснозначных функций, мы получим

Сама возможность такого интегрирования остается под вопросом.

Эффективные характеристики находим элементарно:

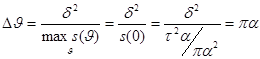
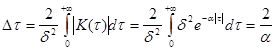
Задача 2. «Белым шумом» называется стационарный широком смысле процесс с постоянной спектральной плотностью на всех частотах . Белый шум физически неосуществим, поскольку его дисперсия бесконечна. Пусть x(t)- стационарный в широком смысле процесс со спектральной плотностью следующего вида

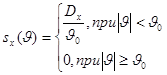
(низкочастотный белый шум).

Найти ковариационную функцию данного процесса и выяснить, является ли низкочастотный белый шум дифференцируемым.

Решение. По формуле (7) имеем:

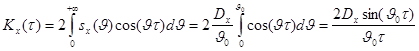
Вычислим вторую производную от ковариационной функции и оценим ее, поскольку для дифференцируемости стационарного в широком смысле случайного процесса необходимо и достаточно существования второй производной автоковариационной функции при

Разложив функцию по степеням в окрестности точки , мы получим следующее представление в виде ряда для ковариационной функции:

Значит,

Так как ряды для равномерно сходятся на любом отрезке, содержащем точку , то из последнего имеем, что

Производную данную можно найти несколько иначе, но без привлечения разложений функции не обойтись. Действительно, непосредственное дифференцирование дает:

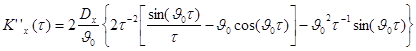
Очевидно, что .Можно показать, что

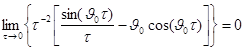
Следовательно, мы получим тот же результат (7).

В силу конечности процесс является дифференцируемым.

Задача 3. Определить ковариационную функцию, дисперсию и эффективные характеристики стационарного случайного процесса, имеющего спектральную плотность

Решение. Согласно формуле для имеем

(8)

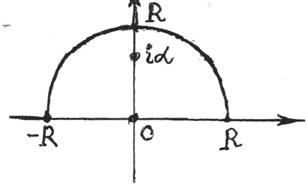
Определим данный интеграл с помощью метода вычетов. Рассмотрим замкнутый контур L, состоящий из отрезка [-R,R] и верхней полуокружности радиуса R с центром в начале координат .

Поскольку то при внутри контура содержится одна особая точка подынтегральной функции

Поэтому

Введем обозначения

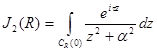
значит,

(9)

Рассмотрим второй интеграл . Произведя в нем замену

приведем его к виду

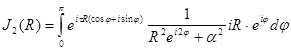
т.е. к виду

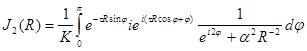
Поскольку 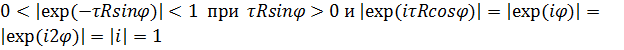, то мы получим оценку

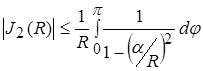
т.е. оценку

Поэтому при и поэтому из (9) будем иметь

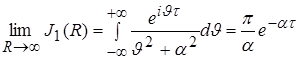
Следовательно, согласно (8) получим, что

Дисперсия процесса равна

.

Определим теперь эффективные характеристики процесса. По определению

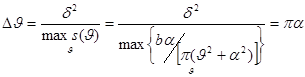
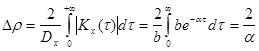
При решении других подобных задач, в более общих случаях, в которых нужно вычислить интегралы вида

(10)

можно воспользоваться леммой Жордана и вытекающим из нее утверждением.

Лемма (Жордан). Пусть функция f(z) регулярна в верхней полуплоскости за исключением конечно числа особых точек есть полуокружность в верхней полуплоскости с центром в точке z=0 и радиусом R:

Тогда

Теорема. Если функция f(z) определена на множестве вещественных чисел R¹ и может быть продолжена на верхнюю полуплоскость с помощью функции f(z), удовлетворяющей условию Леммы Жордана и не имеющей особых точек на вещественной оси, то существует несобственный интеграл (10), причем

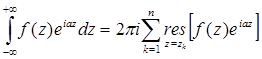
1. Ковариационная функция случайного процесса x(t) имеет вид

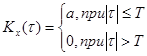
Найти спектральную плотность u, проверив ее свойства, убедиться, что данный процесс не является стационарным в широком смысле.

2. Спектральная плотность случайного процесса x(t) имеет вид

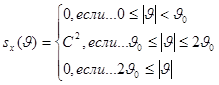
Определить ковариационную функцию

3. Определить дисперсию случайного процесса x(t), если ее спектральная плотность имеет вид

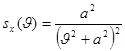
4. Определить ковариационную функцию, дисперсию и эффективную ширину спектра стационарного случайного процесса, имеющего спектральную плотность

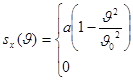
5. Найти спектральную плотность, эффективную ширину спектра и средний интервал корреляции стационарного случайного процесса x(t) с ковариационной функцией

6. Команда y(t), поступающая на пульт управления автоматически управляемого объекта, определяется по формуле

Доказать, что спектральные плотности входного сигнала x(t) и выходного сигнала, команды y(t) связаны уравнением

Найти если