§3.Спектральное представление ковариационной функции стационарного случайного процесса с непрерывным спектра

Периодические колебания величины S(t) называются гармоническими колебаниями, если

S(t)=Asin (ꙍt+ или S(t)=Acos (ꙍt+ ),

где ꙍ=2𝝿ν=2𝝿/T – циклическая или круговая частота колебаний A=max S(t)=const >0 – максимальное значение колеблющейся величины S, называемое амплитудой колебаний , и =-𝝿/2 –постоянные величины – начальные фразы колебаний .

Кинетическая энергия материальной точки массы – m, совершающей прямолинейные гармонические колебания , равна

Кинетическая энергия меняется в пределах [0,.

Гармонические колебания материальной точки на плоскости с нулевой начальной фазой задаются уравнением , её кинетическая энергия в любой момент времени постоянна и равна

.

Рассмотрим теперь интегральное представление (3) из §2 ковариационной функции ясно ,что

,

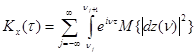где -произвольное разбиение вещественной оси .

Понятно, что,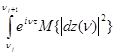

Функция (1)

Задает гармонические колебания на плоскости Q средней амплитудой , кинетической энергией

Как теперь нетрудно понять ,величина (2) имеет смысл среднего значения квадрат модуля амплитуды элементарной гармонической составляющей. В электрофизических приложениях она пропорциональна доли мощности сигнала , вносимый этой составляющей .

Обозначим через среднюю мощность вносимую гармонической составляющей (1) с частотами в интервале (ν,ν+∆ν). Как нетрудно понять,

∆P(ν).

Введем величину S(ν), которая с точностью до постоянного множителя равна пределу отношения средней мощности к ширине этого интервала :

S(ν)=

Если этот предел существует ,то

S(ν)dν

и поэтому

(3)

Интегральное представление (3) получено из приведенных физических соображений , но оно позволяет искать условия ,при которых ковариационная функция представлена в виде(3). Ответ на этот вопрос дает следующая теорема .

Теорема 2.(Бохнер-Хинчин). Для того чтобы непрерывная функция K( представлена собой в ковариационную функцию некоторого стационарного непрерывного( в среднем квадратичном ) процесса , необходимо и достаточно , чтобы она была представлена в виде

(4)

где S(ν) – неотрицательная монотонно неубывающая ограниченная слева функция.

Функция S(ν) называется спектральной функцией .Если она абсолютно непрерывна ,то почти всюду существует S и формула (4) имеет вид

(5)

Выражение (5) есть интегральное преобразование Фурье функции S(ν). Обратное преобразование Фурье

(6)

даёт возможность по ковариационной функции случайного процесса вычислить его спектральную плотность .

Формулы (5)-(6) называются формулами Винера- Хинчина. Выражение ,формула (5) называется спектральным представлением ковариационной функции , а функция - спектральной плотностью случайного процесса.

Стационарный случайный процесс называется случайным процессом с непрерывным спектром ,если для него существует спектральная плотность и справедливы интегральные формулы Винера – Хинчина .