Модуль
2. Тема 3. Плотность распределения и ее свойства
2.
Свойства
Важнейшей
характеристикой непрерывной случайной величины (помимо функции распределения)
является плотность распределения вероятностей.
Определение. Плотностью распределения
вероятностей непрерывной случайной величины ![]() называется
первая производная от ее функции
распределения.
называется
первая производная от ее функции
распределения.
Обозначается
плотность распределения непрерывной случайной величины через
![]() или
или ![]() .
.
Таким
образом, по определению
![]() . (1)
. (1)
Функция ![]() называют также дифференциальной функцией распределения;
она является одной из форм закона распределения непрерывной случайной величины.
называют также дифференциальной функцией распределения;
она является одной из форм закона распределения непрерывной случайной величины.
Установим
вероятностный смысл плотности распределения. Из определения производной следует
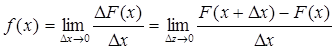 .
.
Но
согласно свойству функции распределения
![]() .
.
Отношение
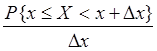
представляет собой среднюю
вероятность, которая приходится на единицу длины участка ![]() . Тогда
. Тогда
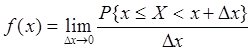 , (2)
, (2)
т.е. плотность распределения
есть предел отношения вероятности попадания случайной величины в промежуток ![]() к длине
к длине ![]() этого
промежутка, когда
этого
промежутка, когда ![]() стремится к нулю. Из равенства (2) следует, что
стремится к нулю. Из равенства (2) следует, что
![]() .
.
Таким
образом, плотность вероятности определяется как функция ![]() , удовлетворяющая условию
, удовлетворяющая условию ![]() . Выражение
. Выражение ![]() называется
элементом вероятности.
называется
элементом вероятности.
Отметим,
что плотность ![]() аналогична
таким понятиям, как плотность распределения масс на оси абсцисс или плотность
тока в теории электричества.
аналогична
таким понятиям, как плотность распределения масс на оси абсцисс или плотность
тока в теории электричества.
Плотность
распределения обладает следующими свойствами:
1.
Плотность
распределения ![]() неотрицательная
функция, т.е.
неотрицательная
функция, т.е. ![]() .
.
2.
Вероятность
попадания непрерывной случайной величины в промежуток ![]() равна
определенному интегралу от ее плотности в пределах от
равна
определенному интегралу от ее плотности в пределах от ![]() до
до ![]() , т.е.
, т.е. 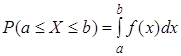 .
.
3.
Функция
распределения непрерывной случайной величины представляется через плотность
распределения в виде: 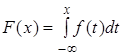 .
.
4.
Несобственный
интеграл от плотности вероятности в бесконечных пределах равен единице, т.е.
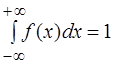 .
.
Можно
дать еще одно определение непрерывной случайной величины.
Определение.
Случайная
величина ![]() называется
непрерывной, если существует неотрицательная функция
называется
непрерывной, если существует неотрицательная функция ![]() такая, что при
любом
такая, что при
любом ![]() функцию
распределения можно представить в виде
функцию
распределения можно представить в виде 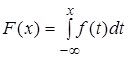 .
.
Наиболее
употребительные непрерывные распределения:
Равномерное
распределение на отрезке [a,b]. Плотность распределения
задается функцией
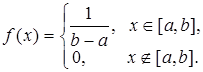
Функция распределения имеет
вид
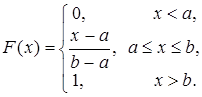
Нормальное (гауссово)
распределение с параметрами ![]() :
:
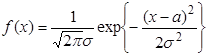 .
.
Функция распределения имеет
вид
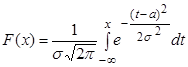 .
.
Пример. Плотность распределения непрерывной случайной
величины ![]() задана функцией
задана функцией
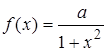 . Найти значение параметра
. Найти значение параметра ![]() .
.
Решение. Согласно свойству 4
плотности, имеем
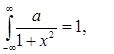 т.е.
т.е. 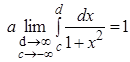
![]()
или ![]() .
.
Следовательно, ![]() .
.