Модуль 2. Тема 1. Случайные величины

1. Случайные величины

2. Закон распределения дискретной случайной величины

3. Многоугольник распределения

Наряду со случайным событием и вероятностью, одним из важнейших понятий теории вероятностей является понятие случайной величины.

Под случайной величиной понимают величину, которая в результате опыта принимает значение случайным образом, которое заранее невозможно предсказать.

Случайные величины обозначают прописными латинскими буквами X, Y, Z,… или строчными греческими буквами и т.д., а принимаемые значения соответственно малыми буквами

Примерами случайных величин могут служить: число очков, появившихся при бросании игральной кости, число выстрелов до первого попадания в цель, рост человека, курс доллара и т.д.

Определение. Случайная величина, принимающая конечное и счетное множество значений, называется дискретной. А если же множество возможных значений случайной величины несчетно, то такая величина называется непрерывной.

Получается, что дискретная случайная величина принимает отдельные изолированные друг от друга значения, а непрерывная случайная величина может принимать любые значения из некоторого промежутка.

Примером дискретной случайной величины может служить число выстрелов до первого попадания, а примером непрерывной случайной величины может служить время безотказной работы прибора, так как ее возможные значения принадлежат промежутку , где .

Дадим определение случайной величины, исходя из теоретико-множественной трактовки основных понятий теории вероятностей.

Определение. Случайной величиной называется числовая функция, определенная на пространстве элементарных событий , которая каждому элементарному событию ставит в соответствие число , т.е. .

Наиболее употребительные дискретные распределения:

Биномиальное распределение. Случайная величина – число появлений некоторого события А в независимых испытаниях с вероятностью появления события А в каждом испытании. Она может принимать значения . Соответствующие вероятности:

,

где .

Гипергеометрическое распределение. Пусть имеется некоторое множество из элементов, среди которых элементов, обладающих некоторым свойством . Из всего множества выбирают случайно элементов без возвращения. Случайная величина – число элементов со свойством среди выбранных может принимать значения . Соответствующие вероятности вычисляются по формуле:

,

где n, M и N —натуральные числа.

Распределение Пуассона. Случайная величина может принимать значения . Соответствующие вероятности:

,

где .

Геометрическое распределение. Производятся независимые испытания, в каждом из которых с вероятностью может наступить (с вероятностью не наступит) некоторое событие А. Случайная величина – число испытаний до первого появления («успеха») события А. Может принимать значения Соответствующие вероятности:

,

где .

Пример. Опыт состоит в бросании монеты 2 раза. Тогда , , , , . Можно рассмотреть случайную величину - число появлений герба. Случайная величина является функцией от элементарного события . . - дискретная случайная величина со значениями с вероятностями соответственно , , .

Определение. Любое правило, позволяющее находить вероятности произвольных событий F (F - алгебра событий пространства ), в частности указывающие вероятности отдельных значений случайной величины или множества этих значений, называется законом распределения случайной величины.

Пусть - дискретная случайная величина, которая принимает значения с вероятностями , где . Закон распределения дискретной случайной величины удобно задать с помощью формулы , определяющей вероятность того, что в результате опыта случайная величина примет значение . Для дискретной случайной величин закон распределения может быть задан в виде таблицы распределения:

X			….		….
P			….		…

где первая строка содержит все возможные значения случайной величины, а вторая - их вероятности. Такую таблицу называют рядом распределения.

Так как события несовместны и образуют полную группу, то сумма их вероятностей равна 1, т.е. .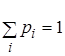

Закон распределения дискретной случайной величины можно задать графически, если на оси абсцисс отложить возможные значения случайной величины, а на оси ординат - вероятности этих значений. Ломаную, соединяющую последовательно точки

называют многоугольником распределения.

Таким образом, случайная величина дискретна, если существует конечное или счетное множество чисел , таких, что и .

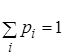Определим математические операции над дискретными случайными величинами.

Суммой (разностью, произведением) дискретной случайной величины , принимающей значения с вероятностями , и дискретной случайной величины , принимающей значения с вероятностями , , называется дискретная случайная величина

,

принимающая значения с вероятностями для всех указанных значений (здесь - вероятности совместного распределения случайных величин и ). В случае совпадения некоторых сумм , разностей , произведений соответствующие вероятности складываются

Произведением дискретной случайной величины на число называется дискретная случайная величина , принимающая значения с вероятностями .

Определение. Две случайные величины и называют независимыми, если события и независимы для любых ,, т.е.

.

В противном случае их называют зависимыми. Несколько случайных величин называются взаимно независимыми, если закон распределения любой из них не зависит от того, какие значения приняли остальные величины.

Пример. В урне 8 шаров, из которых 5 белых, остальные черные. Из нее наудачу вынимают 3 шара. Найти закон распределения числа белых шаров в выборке.

Решение. Возможные значения случайной величины Х- числа белых шаров в выборке есть 0, 1, 2, 3. Их соответствующие вероятности:

.

Закон распределения запишем в виде таблицы.

X	0	1	2	3
р	1/56	15/56	30/56	10/56

Контроль: 1/56+15/56+30/56+10/56=1.