Модуль
1. Тема
9. Независимые испытания. Схема Бернулли
1.
Серия независимых
испытаний Бернулли
Серия
независимых испытаний Бернулли
С
понятием «независимых событий» связано понятие «независимых испытаний»
(опытов).
Несколько
опытов называются независимыми, если их исходы представляют собой независимые
события (независимые в совокупности).
Другими
словами, если проводится несколько испытаний, т.е. опыт выполняется при данном
комплексе условий многократно (такое явление называется последовательностью
испытаний), причем вероятность наступления некоторого события А в каждом
испытании не зависит от исходов других испытаний, то такие испытания называются независимыми.
Примерами
независимых испытаний могут служить: многократное подбрасывание монеты,
стрельба (![]() -раз) по мишени без поправок на ранее допущенную ошибку при
новом выстреле.
-раз) по мишени без поправок на ранее допущенную ошибку при
новом выстреле.
При
практическом применении теории вероятностей часто используется стандартная
схема, называемая схемой Бернулли или схемой независимых испытаний.
Событие А, которое может произойти при
выполнении некоторых условий S, называют иначе успехом. Вероятность такого
события обозначают ![]() , т.е.
, т.е. ![]() . А противоположное ему событие
. А противоположное ему событие ![]() называют
неудачей. Вероятность такого события обозначают
называют
неудачей. Вероятность такого события обозначают ![]() , т.е.
, т.е. ![]() .
.
Последовательность
n независимых
испытаний, в каждом из которых может произойти некоторое событие А с вероятностью ![]() или
противоположное ему событие
или
противоположное ему событие ![]() с вероятностью
с вероятностью ![]() , называется схемой
Бернулли.
, называется схемой
Бернулли.
Например,
при стрельбе по мишени: событие А - попадание
(успех), событие ![]() - промах (неудача); при обследовании n изделий
на предмет годности: А - деталь
годная (успех), событие
- промах (неудача); при обследовании n изделий
на предмет годности: А - деталь
годная (успех), событие ![]() - деталь бракованная (неудача) и т.д.
- деталь бракованная (неудача) и т.д.
В каждом
таком опыте последовательность элементарных исходов состоит только из двух
элементарных событий, т.е. ![]() , где
, где ![]() неудача,
неудача, ![]() успех, при этом
успех, при этом ![]() ,
, ![]() . Вероятности этих событий обозначают через
. Вероятности этих событий обозначают через ![]() и
и ![]() . Множество элементарных исходов для n опытов состоит из
. Множество элементарных исходов для n опытов состоит из ![]() элементов.
Например, при n=3, т.е. опыт повторяется 3 раза,
элементов.
Например, при n=3, т.е. опыт повторяется 3 раза, ![]() . Вероятность каждого элементарного события
определяется однозначно. По теореме умножения вероятность события, скажем
. Вероятность каждого элементарного события
определяется однозначно. По теореме умножения вероятность события, скажем ![]() , равна
, равна ![]() .
.
Простейшая
задача, относящаяся к схеме Бернулли, состоит в определении вероятности того,
что в n
независимых испытаниях событие А
наступит m раз ![]() . Обозначается искомая вероятность
. Обозначается искомая вероятность ![]() .
.
Например,
при бросании игральной кости 3 раза ![]() означает
вероятность того, что в 3-х опытах событие
означает
вероятность того, что в 3-х опытах событие ![]() – выпадение часла очков 4- произойдет ровно 2 раза. Очевидно,
– выпадение часла очков 4- произойдет ровно 2 раза. Очевидно,
![]()
Теорема. Если производятся n независимых испытаний, в каждом из которых
вероятность появления события ![]() равна
равна ![]() , а вероятность его непоявления равна
, а вероятность его непоявления равна ![]() , то вероятность того, что событие
, то вероятность того, что событие ![]() произойдет ровно m раз определяется формулой Бернулли
произойдет ровно m раз определяется формулой Бернулли
![]() (1)
(1)
Доказательство.
Вероятность одного сложного события, состоящего в том, что событие
![]() в
в ![]() независимых опытах появится
ровно m раз в
первых m опытах
и не появится (n-m) раз в остальных опытах
независимых опытах появится
ровно m раз в
первых m опытах
и не появится (n-m) раз в остальных опытах ![]() по теореме умножения
вероятностей равна
по теореме умножения
вероятностей равна ![]() . Вероятность появления события
. Вероятность появления события ![]() снова m раз, но в другом порядке ( например
снова m раз, но в другом порядке ( например ![]() ) будет той же самой, т.е.
) будет той же самой, т.е. ![]() .
.
Число
таких сложных событий- в n опытах m раз встречается событие А в различном порядке-
равно числу сочетаний из n по m, т.е. ![]() . Так
как все эти сложные события несовместны, то по теореме сложения вероятностей
искомая вероятность равна сумме вероятностей всех возможных сложных событий,
т.е.
. Так
как все эти сложные события несовместны, то по теореме сложения вероятностей
искомая вероятность равна сумме вероятностей всех возможных сложных событий,
т.е.
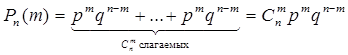 , m=0,1,…,n.
, m=0,1,…,n.
Пример1. Монету бросают 10 раз. Какова
вероятность того, что герб выпадет: а) 4 раза; б) ни разу; в) хотя бы один раз.
Решение. Вероятность успеха в одном «испытании» (при
одном бросании монеты) равна 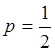 , неудачи
, неудачи 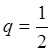 . Тогда по формуле (1):
. Тогда по формуле (1):
а) 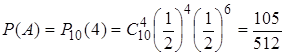 , где А –
событие, что герб выпадет 4 раза.
, где А –
событие, что герб выпадет 4 раза.
б) 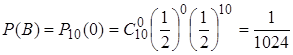 , где В –
событие, что герб ни разу не выпадет.
, где В –
событие, что герб ни разу не выпадет.
в) ![]() , где С –
событие, что герб выпадет хотя бы один раз.
, где С –
событие, что герб выпадет хотя бы один раз.
Вероятности ![]() (1.10.1)
являются коэффициентами при
(1.10.1)
являются коэффициентами при ![]() в разложении
в разложении ![]() по формуле бинома
Ньютона:
по формуле бинома
Ньютона:
![]() .
.
Поэтому
совокупность вероятностей ![]() называют
биномиальным законом распределения вероятностей, а функцию
называют
биномиальным законом распределения вероятностей, а функцию ![]() производящей функцией.
производящей функцией.
Если в
серии из n
независимых опытов, в каждом опыте может произойти одно и только одно из ![]() событий
событий ![]() с соответствующими
вероятностями
с соответствующими
вероятностями ![]() ,
, 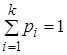 , то вероятность того, что в
этих опытах событие
, то вероятность того, что в
этих опытах событие ![]() появится
появится ![]()
![]() раз, событие
раз, событие ![]() появится
появится ![]() раз,…., событие
раз,…., событие ![]() появится
появится ![]() раз, равна
раз, равна
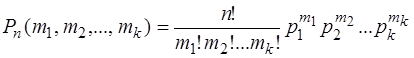 ,
,
где ![]() . Эти вероятности называются полиномиальным
распределением.
. Эти вероятности называются полиномиальным
распределением.
Определение. Число ![]() , при котором функция
, при котором функция ![]() ,
, ![]() , принимает максимальное значение, называется наивероятнейшим числом «успехов».
, принимает максимальное значение, называется наивероятнейшим числом «успехов».
Число ![]() определяют
следующим образом: если
определяют
следующим образом: если ![]() - не целое число, то
- не целое число, то ![]() равно ближайшему
целому числу, большему чем
равно ближайшему
целому числу, большему чем ![]() ; если
; если ![]() - целое число, то
принимает два значения
- целое число, то
принимает два значения ![]() и
и ![]() .
.
Пример 2. Стрелок стреляет по мишени с
вероятностью попадания равной 0,8. Сделано 20 выстрелов. Определить
наивероятнейшее число попаданий в цель.
Решение. Здесь ![]() ,
, ![]() ,
, ![]() . Следовательно,
. Следовательно,
![]() , т. е.
, т. е. ![]()
Так как ![]() - целое число,
то
- целое число,
то ![]() .
.
Использование
формулы Бернулли ![]() при больших
значениях n и m
вызывает большие трудности, так как это связано с громоздкими
вычислениями. В таких случаях подсчитать результат практически невозможно.
Пользоваться формулой Бернулли вызывает затруднения также при малых значениях p и q. В
таких случаях, возникает необходимость в отыскании приближенных формул для вычисления
при больших
значениях n и m
вызывает большие трудности, так как это связано с громоздкими
вычислениями. В таких случаях подсчитать результат практически невозможно.
Пользоваться формулой Бернулли вызывает затруднения также при малых значениях p и q. В
таких случаях, возникает необходимость в отыскании приближенных формул для вычисления ![]() , обеспечивающих необходимую точность. Такие формулы
дают нам предельные теоремы; на них основаны так называемые асимптотические
формулы, которые при больших значениях числа испытаний дают сколь угодно малую
относительную погрешность. Рассмотрим три такие предельные теоремы.
, обеспечивающих необходимую точность. Такие формулы
дают нам предельные теоремы; на них основаны так называемые асимптотические
формулы, которые при больших значениях числа испытаний дают сколь угодно малую
относительную погрешность. Рассмотрим три такие предельные теоремы.
Теорема Пуассона. Если
число испытаний неограниченно увеличивается (![]() ) и вероятность p
наступления события А в каждом испытании неограниченно уменьшается (
) и вероятность p
наступления события А в каждом испытании неограниченно уменьшается (![]() ), но так, что произведение
), но так, что произведение ![]() является
постоянной величиной
является
постоянной величиной ![]() , то вероятность
, то вероятность ![]() удовлетворяет
предельному равенству
удовлетворяет
предельному равенству
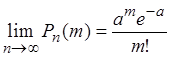 . (2)
. (2)
Выражение
(2) называется асимптотической формулой Пуассона.
Доказательство. Преобразуем
формулу Бернулли с учетом того, что ![]() :
:
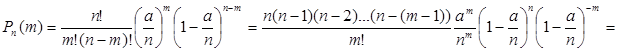
![]() Переходя к пределу при
Переходя к пределу при ![]() , получим
, получим 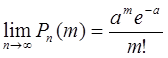 .
.
Из
предельного равенства (2) при больших ![]() и малых
и малых ![]() вытекает приближенная
формула Пуассона
вытекает приближенная
формула Пуассона
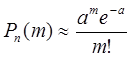 ,
, ![]() ,
, ![]() . (3)
. (3)
Формула
(3) применяется, когда вероятность успеха ![]() крайне мала, т.е сам по себе успех является редким событием.
Приближенную формулу (3) обычно используют, когда
крайне мала, т.е сам по себе успех является редким событием.
Приближенную формулу (3) обычно используют, когда ![]() , а
, а ![]() . Формула Пуассона находит применение в теории массового
обслуживания.
. Формула Пуассона находит применение в теории массового
обслуживания.
Пример 1. С винного завода отправили в Москву 1500 бутылок вина.
Вероятность того, что в пути бутылка может разбиться, равна 0,002. Найти
вероятность того, что в пути будет разбито не более 4-х бутылок.
Решение. Искомая
вероятность равна
![]() .
.
Так как n=1500, p=0.002, то ![]() . Вероятность события
. Вероятность события ![]() найдем
по формуле Пуассона (3):
найдем
по формуле Пуассона (3):
![]()
![]() .
.
Формулу
Пуассона можно считать математической моделью простейшего потока событий.
Потоком событий
называют последовательность событий, наступающих в случайные моменты времени
(например, поток посетителей в парикмахерской, поток вызовов на телефонной
станции, поток отказов элементов, поток обслуженных абонентов).
Поток
событий, обладающих свойствами стационарности, ординарности и отсутствия
последствия называется простейшим (пуассоновским) потоком.
Свойство
стационарности
означает, что вероятность появления ![]() событий на
участке времени длины
событий на
участке времени длины ![]() зависит только от его
длины (т.е. не зависит от начала его отсчета).
Следовательно, среднее число событий, появляющихся
в единицу времени, так называемая интенсивность
зависит только от его
длины (т.е. не зависит от начала его отсчета).
Следовательно, среднее число событий, появляющихся
в единицу времени, так называемая интенсивность ![]() потока, есть
величина постоянная:
потока, есть
величина постоянная: ![]() .
.
Свойство
ординарности
означает, что событие появляется не группами, а поодиночке. Другими словами,
вероятность появления более одного события за малый промежуток времени ![]() пренебрежительно
мала по сравнению с вероятностью появления только одного события (например,
поток катеров, подходящих к причалу, ординарен).
пренебрежительно
мала по сравнению с вероятностью появления только одного события (например,
поток катеров, подходящих к причалу, ординарен).
Свойство
отсутствия
последствия означает, что вероятность появления ![]() событий на
любом отрезке времени длины
событий на
любом отрезке времени длины ![]() не зависит от того,
сколько событий появилось на любом другом непересекающимся с ним отрезке
(говорят: «будущее» потока не зависит от прошлого, например, поток людей, входящих в
супермаркет).
не зависит от того,
сколько событий появилось на любом другом непересекающимся с ним отрезке
(говорят: «будущее» потока не зависит от прошлого, например, поток людей, входящих в
супермаркет).
Вероятность
появления ![]() событий
простейшего потока за время продолжительностью
событий
простейшего потока за время продолжительностью ![]() определяется формулой
Пуассона
определяется формулой
Пуассона
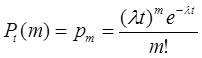
Пример 2. Телефонная станция
обслуживает 2000 абонентов. Вероятность позвонить любому абоненту в течении
часа равна 0,003. Какова вероятность того, что в течении часа позвонят 5
абонентов?
Решение. Среднее
число позвонивших в течении часа абонентов равно ![]() . Тогда
. Тогда 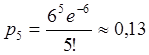 .
.
В тех
случаях, когда число испытаний велико, а вероятность p не близка к нулю, для вычисления биномиальных
вероятностей используются приближенные формулы, получаемые на основе теоремы
Муавра-Лапласа.
Локальная теорема Муавра-Лапласа. Если
вероятность p наступления события А в каждом испытании
постоянна и отлична от нуля и единицы и величина 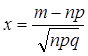 при
при ![]() ограничена, тогда
справедливо равенство
ограничена, тогда
справедливо равенство
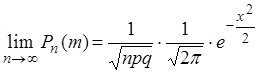 , где
, где 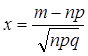 .
.
Отсюда
можно получить приближенную формулу
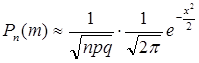 , где
, где 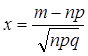 . (4)
. (4)
Равенство
(4) тем точнее, чем больше ![]() .
.
Выражение 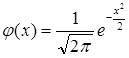 называется
функцией Гаусса, а ее график- кривой вероятностей. Тогда формулу (4) можно
переписать в виде
называется
функцией Гаусса, а ее график- кривой вероятностей. Тогда формулу (4) можно
переписать в виде
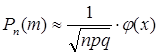 , где
, где
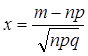 . (5)
. (5)
Для функции ![]() составлены
таблицы значений (они приводятся как Приложения в книгах по теории
вероятностей) При использовании таблицы следует учитывать, что:
составлены
таблицы значений (они приводятся как Приложения в книгах по теории
вероятностей) При использовании таблицы следует учитывать, что:
а)
функция ![]() четная, т.е.
четная, т.е. ![]() ;
;
б) при ![]() можно считать,
что
можно считать,
что ![]() .
.
Пример 3. Вероятность попадания в
мишень при одном выстреле для данного стрелка равна 0,7. Найти вероятность
того, что при 200 выстрелах мишень будет поражена 160 раз.
Решение. Здесь ![]() . Применим формулу (5). Имеем
. Применим формулу (5). Имеем ![]() . Следовательно,
. Следовательно, 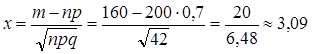 . Учитывая, что
. Учитывая, что ![]() , получаем
, получаем
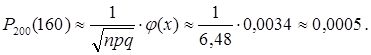
В тех
случаях, когда требуется вычислить вероятность того, что в ![]() независимых испытаниях
событие А появится не менее
независимых испытаниях
событие А появится не менее ![]() , но не более
, но не более ![]() раз, т.е.
раз, т.е. ![]() , используют интегральную теорему Муавра-Лапласа.
, используют интегральную теорему Муавра-Лапласа.
Интегральная теорема Муавра-Лапласа. Если вероятность p наступления события А в каждом испытании постоянна и отлична от нуля и единицы, то для
схемы Бернулли при ![]() и для любых
и для любых ![]() и
и ![]() справедливо
справедливо
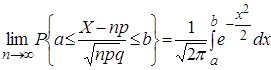
Отсюда, в частности, следует, что для вычисления вероятности ![]() можно
использовать формулу
можно
использовать формулу
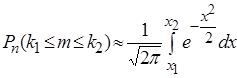 , где
, где 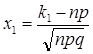 ,
, 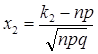 (6)
(6)
Равенство
(6) тем точнее, чем больше ![]() .
.
Используя
функцию Гаусса, равенство (6) можно записать в виде
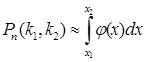 .
.
Однако
для упрощения вычислений, при использовании формулы (6), вводят специальную
функцию
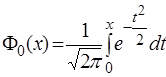 , (7)
, (7)
называемую нормированной
функцией Лапласа. Функция (7) нечетная, т.е. 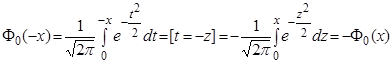 .
.
При ![]() можно
считать, что
можно
считать, что ![]()
Выразим
правую часть равенства (6) через функцию Лапласа (7).
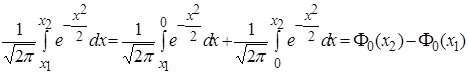
Формула
(6) принимает вид
![]() , где
, где 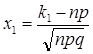 ,
, 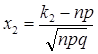 .
.