Модуль 1. Тема 7. Условные вероятности

4. Независимые события

Пусть события A и B несовместные, причем вероятности этих событий известны. Как найти вероятность того, что наступит либо событие А, либо событие В. Ответ на этот вопрос дает аксиома сложения А3 или свойство 4 при классическом определении вероятности.

В случае, когда события не являются несовместными, справедлива теорема

Теорема (сложения). Вероятность суммы двух совместных событий равна сумме их вероятностей без вероятности их произведения,

. (1)

Доказательство. Представим события А+В и В в виде суммы двух несовместных событий:

, (2)

. (3)

Тогда согласно аксиоме А3 и из (2) и (3) имеем и . Отсюда следует .

Формула (1) справедлива для любых событий А и В.

В случае трех событий формула сложения имеет вид:

Пример. Бросают две игральные кости. Какова вероятность появления хотя бы одной шестерки?

Решение. Введем события: А-появление шестерки на первой кости, В- на второй кости. Тогда А+В- появление хотя бы одной шестерки при бросании двух игральных костей. События А и В совместные. Тогда .

Условная вероятность

Пусть А и В- два события, рассматриваемые в данном опыте. Наступление одного события (скажем А) может влиять на возможность наступления другого B. Для характеристики зависимости одних событий от других вводится понятие условной вероятности.

Определение. Условной вероятностью события В при условии, что произошло событие А, называется отношение вероятности произведения этих событий к вероятности события А, причем , обозначается символом .

Таким образом, по определению

(4)

Вероятность , в отличие от условной, называется безусловной.

Аналогично определяется условная вероятность события А при условии В, т.е. :

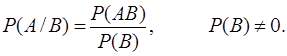(5)

Отметим, что условная вероятность удовлетворяет аксиомам Колмогорова :

1) ;

2) ;

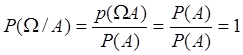3) Ø.

Для условной вероятности справедливы все следствия (свойства) из аксиом. Формула (4) принимается по определению при аксиоматическом определении вероятности. В случае классического (геометрического, статистического) определения она может быть доказана.

Пример 1. В урне 2 белых и 7 черных шаров. Из нее последовательно вынимают два шара. Какова вероятность того, что 2-й шар окажется белым при условии, что 1-й шар был черным?

Решение. Пусть А- 1-й шар черный, В- 2-й шар белый. Так как событие А произошло, то в урне осталось 8 шаров, из которых 2 белых. Поэтому .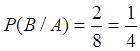

Из определений условной вероятности (4) и (5) следует, что

, (6)

т.е. вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого при условии, что первое событие произошло.

Равенство (6) называется правилом или теоремой умножения вероятностей. Это правило обобщается на случай n событий:

Так, для трех событий получаем

Пример 2. В коробке находятся 4 белых, 3 синих и 2 черных шара. Наудачу последовательно вынимают 3 шара. Какова вероятность того, что 1-й шар будет белым, 2-й шар будет синим, 3-й шар будет черным?

Решение. Введем следующие события: - первым вытащили белый шар, - вторым синий, - третьим черный. Тогда . По правилу умножения вероятностей

Правило умножения вероятностей имеет простой вид, если события, образующие произведение, независимые.

Определение. Событие А называется независимым от события В, если его условная вероятность равна безусловной, т.е. если выполняется равенство

. (7)

Лемма. Если событие А не зависит от события В, то событие В не зависит от события А.

Доказательство. Из равенства

с учетом (7), следует

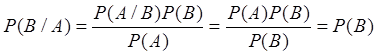т.е .

А это означает, что событие В не зависит от события А.

Можно дать следующее (новое) определение независимости событий.

Определение. Два события называются независимыми, если появление одного из них не меняет вероятность появления другого.

Для независимых событий правило умножения вероятностей принимает вид:

т.е. вероятность произведения двух независимых событий равна произведению вероятностей этих событий.

Можно показать, что если события А и В независимые, то независимы также события и , и , и .

Понятие независимости может быть распространено на случай n событий.

Определение. События называются независимыми в совокупности, если каждое из них не зависит от произведения любого числа остальных событий и от каждого в отдельности. В противном случае называются зависимыми. Для независимых событий условные вероятности равны безусловным:

Определение. События называются попарно-независимыми, если для любых двух событий и () выполняется:

Из попарной независимости событий не следует их независимость в совокупности. (Обратное верно).

Пример 3. Два стрелка стреляют по мишени залпом. Вероятность попадания для первого стрелка равно 0.9, а для второго 0.8. Найти вероятность того, что оба стрелка попадут в мишень.

Решение. Пусть А- первый попадет в мишень, а В- второй попадет в мишень. Нужно найти вероятность события С=АВ. События независимые. Следовательно вероятность их совместного появления равно произведению вероятностей этих событий .