Модуль 1. Тема 5. Относительная частота

Относительная частота наряду с вероятностью принадлежит к основным понятиям теории вероятностей.

Классическое определение вероятности предполагает, что число элементарных исходов испытания конечно. На практике же весьма часто встречаются испытания, число возможных исходов которых бесконечно. Уже это обстоятельство и указывает на ограниченность классического определения.

Наиболее слабая сторона классического определения состоит в том, что очень часто невозможно представить результат испытания в виде совокупности элементарных событий. Еще труднее указать основания, позволяющие считать элементарные события равновозможными. По этой причине наряду с классическим определением вероятности используют и другие определения вероятности, в частности статистическое определение: в качестве вероятности события принимают относительную частоту или число близкое к ней.

Относительной частотой события называют отношение числа испытаний, в которых событие появилось, к общему числу фактически произведенных испытаний. Таким образом, относительная частота события А определяется формулой

,

где m-число появлений события, n-общее число испытаний.

Таким образом вероятность вычисляют до опыта, а относительную частоту после опыта.

Пример. Отдел технического контроля обнаружил 3 нестандартных деталей в партии из 80 случайно отобранных деталей. Относительная частота появления нестандартных деталей W(A)=3/80.

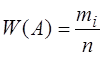Длительные наблюдения показали, что если в одинаковых условиях производят опыты, в каждом из которых число испытаний достаточно велико и в каждом -ом опыте определяют относительную частоту события , то относительная частота обнаруживает свойство устойчивости.

Это свойство состоит в том, что в различных опытах относительная частота изменяется мало (тем меньше, чем больше произведено испытаний), колеблясь около некоторого постоянного числа. Это постоянное число есть вероятность появления события.

Таким образом, если опытным путем установлена относительная частота, то полученное значение можно принять за приближенное значение вероятности.

Например, если в результате достаточно большого числа испытаний оказалось, что относительная частота весьма близка к числу 0,4, то это число можно принять за статистическую вероятность события. Все свойства вероятности, вытекающие из классического определения, сохраняются и при статистическом определении вероятности.

Для существования статистической вероятности события А требуется:

а) возможность, хотя бы принципиально, производить неограниченное число испытаний, в каждом из которых событие А наступает или не наступает;

б) устойчивость относительных частот появления А в различных сериях достаточно большого числа испытаний.

Недостатком статистического определения является неоднозначность статистической вероятности.