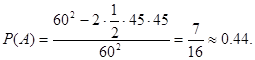Модуль 1. Тема 4. Геометрические вероятности

Чтобы преодолеть недостаток классического определения вероятности, состоящий в том, что оно не применимо к испытаниям с бесконечным числом исходов, в некоторых случаях вводят геометрические вероятности- вероятности попадания точки в область (отрезок, часть плоскости и т.д.).

Пусть отрезок составляет часть . На отрезок наудачу поставлена точка. Это означает выполнение следующих предположений: поставленная точка может оказаться в любой точке отрезка , вероятность попадания точки на отрезок пропорциональна длине этого отрезка и не зависит от его расположения относительно всего отрезка . В этих предположениях вероятность попадания точки на отрезок определяется равенством

.

Пример 1. На отрезок ОА длины числовой оси Ох на удачу поставлена точка . Найти вероятность того, что меньший из отрезков ОВ и ВА имеет длину, большую /3.

Решение. Разобьем отрезок ОА точками C и D на 3 равные части. Требование задачи будет выполнено, если точка попадет на отрезок CD длины L/3. Искомая вероятность

Рассмотрим на плоскости некоторую область , имеющую площадь , и внутри области область D с площадью . В области случайно выбирается точка X. Этот выбор можно интерпретировать как бросание точки X в область . При этом попадание точки X в область - достоверное событие, в D- случайное событие. Предполагается, что все точки области равноправны (все элементарные события равновозможные), т.е. что брошенная точка может попасть в любую точку области и вероятность попасть в область D пропорциональна площади этой области и не зависит от ее расположения и формы. Пусть событие A={XD}, т.е. брошенная точка попадет в область D.

Геометрической вероятностью события A называется отношение площади области D к площади области , т.е.

.

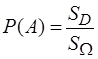Геометрическое определение вероятности события применимо и в случае, когда области и D некоторые объемы. В этом случае:

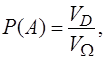
где V объем соответствующей области. Все три формулы можно записать в виде:

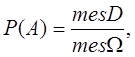
где через mes обозначена мера области.

Геометрическая вероятность обладает всеми свойствами, присущими классическому определению.

Пример 2. Внутрь круга радиуса R наудачу брошена точка. Найти вероятность того, что точка окажется внутри вписанного в круг квадрата.

Решение. Вероятность того, что точка окажется внутри вписанного в круг квадрата равна отношению площади данного квадрата к площади круга, а именно

.

Пример 3. (Задача о встрече). Два человека договорились о встрече в течении определенного часа. Пришедший первым ждет второго в течении 15 минут, после чего уходит. Найти вероятность того, что встреча состоится, если в течении указанного промежутка каждый выбирает момент своего прихода наудачу.

Решение. Пусть x- время прихода первого, а y- время прихода второго. Возможные значения x и y: , которые на плоскости Oxy определяют квадрат со стороной равной 60. Точки этого квадрата изображают время встречающихся (рис.2).

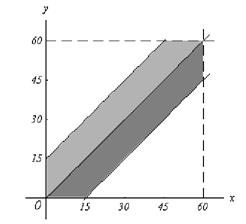
Рис. 2

Тогда ; все исходы равновозможны, так как лица приходят наудачу. Событие А- лица встретятся, если разность между моментами прихода будет не более 15 мин. (по модулю), т.е. , т.е. . Это множество точек есть множество благоприятствующих встрече исходов. Искомая вероятность равно: