Модуль 1. Тема 3. Основные формулы комбинаторики

Комбинаторика - раздел математики, посвященный решению задач выбора и расположения элементов некоторого, обычно конечного, множества. Выбор элементов и их расположение подчинены некоторым условиям. Каждое условие определяет некоторую схему (комбинацию), составленную из элементов исходного множества, называемую комбинаторной схемой. Целью комбинаторики является разработка методов подсчета числа элементов различных множеств, числа комбинаций из элементов множества.

Комбинаторные методы широко применяются в теории вероятностей, статистике, экономике, физике, теории игр, химии, биологии и многих других областях науки, техники и производства.

Основные правила комбинаторики. Рассмотрим два общих правила, с помощью которых решаются задачи комбинаторики – правило суммы и правило произведения.

Правило суммы: пусть имеется попарно непересекающихся множеств , содержащих элементов соответственно. Число способов, которыми можно выбрать один элемент из всех этих множеств, равно

Выборка. Упорядоченная последовательность (допускающая повторения) элементов из множества А. называется выборкой объема из множества А.

Правило произведения: пусть имеется множеств содержащих элементов соответственно. Число способов, которыми можно последовательно выбрать по одному элементу из каждого множества, т. е. построить (), где (i = 1, 2, · · · , ), равно .

Размещения. Из некоторого конечного множества M, содержащего элементов можно извлекать с возвращениями или без возвращений наборы по элементов. Если выборка производится без возврата, то элементы в каждом наборе не повторяются. В случае возврата элементы естественно могут повторяться.

Определение. Наборы () из элементов множества M, содержащего элементов, осуществляемые выбором без возвращения, называются размещениями из элементов по .

Согласно определению два размещения из по могут отличаться как элементами, так и их порядком (размещения () и () различные).

Число всех размещений из по обозначается символом .

Теорема. .

Доказательство. В упорядоченном наборе () первый элемент может быть выбран способами ( возможностей). После выборе элемент может быть выбран из оставшихся способами, и так далее. Используя правило умножении комбинаторики, получим искомую формулу.

Пример 1. .

Перестановки.

Определение. Размещения () из по называются перестановками из элементов (поскольку все такие размещения состоят из одних и тех же элементов и отличаются только порядком элементов).

Число перестановок из элементов обозначается и равно:

Пример 2. Сколькими способами можно расположить в ряд на книжной полке семь различных книг?

Решение. Число всех таких расположений равно числу всех перестановок множества, состоящего из семи элементов, т. е. числу

= 7! = 5040.

Размещения с повторениями.

Определение. Размещение элементов из , выбираемых с возвратом каждого элемента, называется размещением с повторениями (поскольку каждый элемент может повторяться).

Так как каждый элемент набора имеет возможностей выбора, то для числа всех размещений с повторениями имеет место формула:

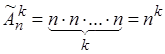Пример 3. Сколькими способами могут пять пассажиров выйти на девяти остановках?

Решение. Каждый из пассажиров может выйти на любой из остановок, поэтому элементы в наборе могут повторяться. Следовательно, искомые наборы есть выборки длины 5 из множества S в 9 элементов. Таким образом, ответ:

Сочетания.

Определение. Подмножество из элементов -элементного множества M (неупорядоченный набор различных элементов) называется сочетанием из по .

Два различных сочетания из по обязательно отличаются хотя бы одним элементом.

Каково число всех сочетаний из по (то есть число всех -элементных подмножеств элементного множества)?

Рассмотрим все сочетания из по . В каждом совершим всевозможные перестановки его элементов. Очевидно, что получим все размещения из по . Таким образом,

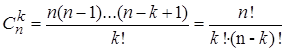Пример 4. Сколькими способами можно составить комиссию в составе из 3 человек, выбирая их из 4 супружеских пар, если:

а) в комиссию могут входить любые 3 из 8 человек;

б) в комиссию не могут входить члены одной семьи?

Решение. а) Если в комиссию могут входить любые 3 из 8 человек, то существует всего таких комиссий:

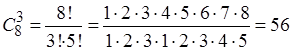б) Если в комиссию не могут входить члены одной семьи, то в ней должны быть представлены 3 из 4 семей. Эти семьи можно выбрать

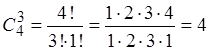
способами. После этого в каждой из них можно 2 способами выбрать представителя – мужа или жену. Следовательно, всего

таких комиссий.

Очевидно, что

, .

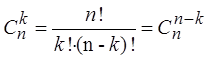В случае = 0 принято соглашение 0! =1 ⇒ .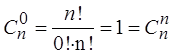

Числа , = 0, 1, . . . , n, называются биномиальными коэффициентами, поскольку являются коэффициентами разложения бинома Ньютона (И. Ньютон, 1643-1727):

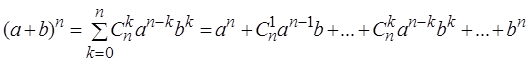Формула бинома Ньютона может быть доказана методом математической индукции.

Замечание 1. Существуют перестановки предметов с повторениями предметов одного типа, – второго, . . . , --го типа; . Их число равно:

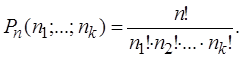
В частности,

Также существуют сочетания из по с повторениями (при выборке элементов с возвратом). Их число равно:

Замечание 2. При повторении элементов в наборе, наборы могут быть любой длины . Например, телефонные номера длины 15 можно выбрать в количестве .