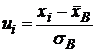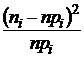Тема 6. Статистическая проверка гипотез

Наиболее часто возникающей задачей при исследовании данных некоторой случайной величины заключается в определении ее функции распределения .

По некоторым предварительным соображениям пусть можно сделать предположение (гипотезу) о неизвестной функции распределения . Например, что она имеет вполне определенный вид или , - неизвестные параметры, которые обычно приходится заранее оценить. Задачей математической статистики является проверка согласованности имеющихся выборочных данных с выдвигаемой гипотезой.

Для проверки этой цели необходимо разрабатывать специальные критерии.

В общем виде процедуру проверки статистической гипотезы можно сформулировать следующим образом.

Итак, имеется выборка

(1)

1. По этой выборке вычисляем выборочные характеристики , , моду, медиану, эмпирическую функцию распределения и другие параметры выборки по необходимости.

2. Строится неотрицательная функция, которая, представляет собой некоторую меру отличия между эмпирической функцией и предполагаемой теоретической (гипотетической) функцией : . Эта функция есть случайная величина. В предположении того, что выдвинутая гипотеза верна, можно найти распределение случайной величины . Функция называется критерием. Меру отличия можно, вообще говоря, выбирать разными способами. Таким образом, для проверки выдвинутой гипотезы могут существовать различные критерии.

3. Задается малое число , настолько малое, что появление события с вероятностью можно считать практически невозможным: - называется уровнем значимости; - определяется из равенства в соответствии с вероятностным распределением критерия и называется критическим значением или пределом значимости. Область, определяемая неравенством , называется критической областью.

4. По выборке (1) вычисляется так называемое наблюдаемое значение критерия и сравнивают с критическим значением .

Если окажется, что , то это означает, что происходит событие с малой вероятностью , т. е. практически невозможное событие. Таким образом, наша гипотеза о равенстве приводит к противоречивому результату – происходит невозможное событие и, поэтому, гипотезу опровергают.

Если , то считают, что нет оснований опровергнуть выдвинутую гипотезу и ее принимают. Гипотезу обозначают: .

Отметим следующее: событие может произойти, в принципе, и в случае, когда наша гипотеза неверна, а событие может произойти когда гипотеза верна. Поэтому не принятие гипотезы () вовсе не означает логического доказательства ее неверности, также, как ее принятие – логического доказательства ее верности.

Однако при малом значении событие является практически невозможным в единичном опыте и, как правило, при этом гипотезу опровергают, в случае же - гипотезу принимают, но она проверятся также с помощью других критериев.

Критерий Пирсона.

Рассмотрим пример проверки гипотезы , когда функция вполне определена, - не содержит неизвестные параметры.

Введем сначала понятие -распределения.

Распределение («хи-квадрат»).

Пусть независимы и распределены , т. е. .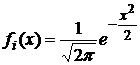

Образуем случайную величину

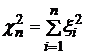Параметр - называется числом степеней свободы.

Плотность распределения этой случайной величины

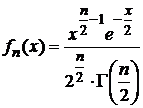, (2)

где - -функция:

, .

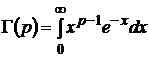Случайная величина 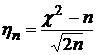, имеет математическое ожидание равное 0 и дисперсию =1.

- асимптотически нормальна .

В критерии Пирсона меру отклонения эмпирической функции от теоретической (гипотетической) строится следующим образом.

Множество значений случайной величины разделим на непересекающихся подмножеств с помощью чисел так, чтобы правый конец -го интервала включался в множество ,

Подсчитываются числа - количество выборочных значений (1), попавших в -й интервал, ; .

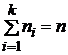Пусть - вероятность попадания случайной величины в -ый интервал: , где и - концы -го интервала, .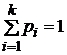

Отношение - частота попадания величин в -ый интервал при наблюдениях, .

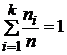Вспомним, что 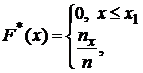где . Отсюда имеем, что - это приращение эмпирической функции на -ом отрезке. В то же время - это приращение теоретической функции на этом отрезке.

Поэтому имеет смысл сравнивать эти две величины: и .

В качестве меры отклонения берут неотрицательную величину

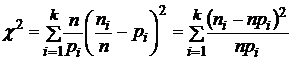(3)

Пирсоном было доказано, что случайная величина (3) в пределе при имеет (хи-квадрат) распределение с плотностью распределения (2) при числе степеней свободы . Составлены таблицы распределения при различных значениях . При достаточно большом можно полагать, что величина (3) имеет приближенно -распределение. Тогда при заданном можно найти критическое значение из условия

Далее по формуле (3) вычисляют наблюдаемое значение и, если гипотезу отвергают, в противном случае принимают.

Пример. Используя критерий Пирсона, при уровне значимости 0,05 проверить, согласуется ли гипотеза о нормальной совокупности с эмпирическим распределением выборки объема :

	5	7	9	11	13	15	17	19	21
	15	26	25	30	26	21	24	20	13

Решение. 1. Найдем выборочную среднюю

и выборочное среднее квадратическое отклонение

2. Вычислим вероятности , учитывая, что , (шаг), , по формуле

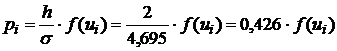Составим таблицу


1	5	-1,62	0,1074	9,1
2	7	-1,2	0,1942	16,5
3	9	-0,77	0,2966	25,3
4	11	-0,35	0,3752	32
5	13	0,08	0,3977	33,9
6	15	0,51	0,3502	29,8
7	17	0,93	0,2589	22
8	19	1,36	0,1582	13,5
9	21	1,78	0,0818	7

3. Сравним эмпирические и теоретические частоты.

Для этого составим таблицу,


1	15	9,1	5,9	34,81	3,8
2	26	16,5	9,5	90,25	5,5
3	25	25,3	-0,3	0,09	0
4	30	32	-2	4	0,1
5	26	33,9	-7,9	62,41	1,8
6	21	29,8	-8,8	77,44	2,6
7	24	22	2	4	0,2
8	20	13,5	6,5	42,25	3,1
9	13	7	6	36	2,1

из которой найдем наблюдаемое значение критерия . По таблице критических точек распределения, по уровню значимости и числе степеней свободы находим критическую точку правосторонней критической области

Так как - гипотезу о нормальном распределении генеральной совокупности отвергаем. Т.е. эмпирические и теоретические частоты различаются значимо.