Тема 2. Статистическая оценка неизвестных параметров распределений

1. Оценка неизвестного параметра

2. Свойства оценок:

состоятельность

несмещенность

эффективность

3. Несмещенность и состоятельность оценок некоторых параметров

Пусть для изучаемой случайной величины известно, что ее функция распределения принадлежит к определенному классу функций распределения , однако параметр (или вектор параметров) неизвестен.

Имеется выборка значений . Необходимо по этой выборке найти оценку неизвестного параметра . Оценка является функцией выборочных значений , т. е. . Следовательно, - случайная величина с распределением, зависящим от параметра . Для конкретной выборки получается одно частное значение случайной величины .

Чтобы была «хорошей» оценкой для , она должна быть достаточно близка к . Это означает, что распределение должно быть сосредоточено около неизвестного параметра с небольшим рассеянием.

Следующие свойства оценок являются математическим выражением их качества.

Состоятельность.

Определение. Если при по вероятности сходится к оцениваемому параметру , то такая оценка называется состоятельной.

Напомним, что сходимость по вероятности означает следующее:

,

или

.

Несмещенность.

Определение. Оценка называется несмещенной оценкой параметра , если

.

Для случайной величины с плотностью это можно записать следующим образом:

_.

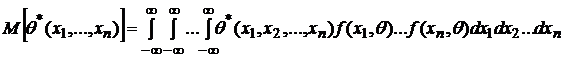В общем случае оценка параметра может иметь некоторое смещение , зависящее от , т. е.

.

Эффективность.

По одним и тем же выборочным данным можно построить различным образом оценки неизвестного параметра .

Возникает вопрос: какая из оценок лучше?

Для сравнения различных оценок будем использовать средний квадрат отклонения . Чем меньше эта величина, тем лучше оценка.

В классе оценок с заданным смещением будем выбирать оценку, для которой величина минимальна, т. е. минимизировать , т. к.

.

- фиксировано. Значит надо минимизировать величину .

Имеется возможность показать для класса оценок для одного и того же параметра , что ограничена снизу некоторым положительным числом , зависящим от функции распределения , объема выборки и смещения .

Определение. Если существует оценка , дисперсия которой равна этой нижней границе , то эта оценка называется эффективной оценкой.

Нижняя граница дисперсии оценки определяется неравенством Рао-Крамера.

Покажем теперь несмещенность и состоятельность оценок некоторых параметров.

Выборочная средняя

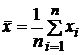
берется в качестве оценки математического ожидания случайной величины .

Теорема 1. Выборочная средняя является несмещенной и состоятельной оценкой для математического ожидания случайной величины, т. е.

и

при .

Доказательство.

Значения являются по определению выборки последовательностью независимых одинаково распределенных случайных величин.

Каждая из случайных величин имеет такое же распределение, как и случайная величина , значениями которой они являются (т. е. ).

Тогда

,

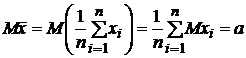т. е. является несмещенной оценкой математического ожидания .

Так как распределены одинаково, то их дисперсии ограничены одной и той же постоянной;

.

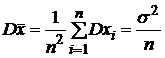Тогда по теореме Чебышева (закон больших чисел) получаем

,

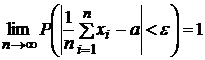т. е. является состоятельной оценкой для математического ожидания .

Теорема доказана.

Выборочная дисперсия

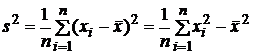
берется в качестве оценки дисперсии генеральной совокупности.

Теорема 2. Выборочная дисперсия не является несмещенной оценкой для дисперсии случайной величины .

Доказательство.

Пусть , . Имеем , .

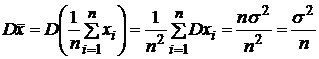Тогда

,

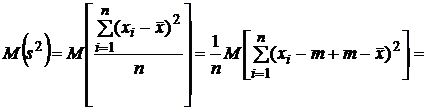
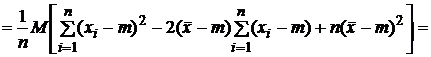
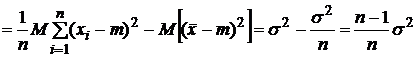так как .

Итак

.

Таким образом, - является смещенной оценкой дисперсии ; смещение .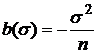

Теорема доказана.

Величина

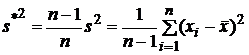
является несмещенной оценкой для , - называют исправленной выборочной дисперсией.

Можно показать, что является состоятельной оценкой для генеральной дисперсии.