Тема 1.
Выборка.
Функция
распределения
и числовые
характеристики
выборки
1.
Выборка
3.
Числовые
характеристики
выборки
Главным
объектом при
статистическом
исследовании
какой –либо случайной
величины ![]() является
выборка
совокупность
полученных в
результате
наблюдений
значений
этой случайной
величины.
является
выборка
совокупность
полученных в
результате
наблюдений
значений
этой случайной
величины.
Под
выборкой мы
будем
понимать
последовательность
независимых
одинаково
распределенных
случайных
величин
![]() . (1)
. (1)
Таким
образом,
определенная
выборка представляет
собой
естественную
математическую
модель
совокупности
из ![]() экспериментальных
значений
некоторой случайной
величины
экспериментальных
значений
некоторой случайной
величины ![]() .
.
Определение
выборки
предполагает,
что наблюдения
производятся
в одинаковых
условиях и,
что
результаты
не зависят
друг от друга.
Величина
![]() -
называется
объемом
выборки.
-
называется
объемом
выборки.
Всевозможные
значения
изучаемого
случайного
признака
называют генеральной
совокупностью.
Выборку (1)
называют
выборкой из
генеральной
совокупности.
Последовательность
(1) расположим
в порядке
возрастания
![]() (2)
(2)
Последовательность
(2) называется вариационным
рядом.
Функция ![]() ,
определенная
по выборке
следующим
образом:
,
определенная
по выборке
следующим
образом:
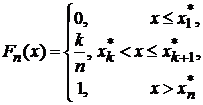
называется
функцией
распределения
выборки, или эмпирической
функцией
распределения.
Геометрически
![]() представляет
собой
ступенчатую
неубывающую
функцию. Она
непрерывна
слева и имеет
точки
разрыва при
значениях
представляет
собой
ступенчатую
неубывающую
функцию. Она
непрерывна
слева и имеет
точки
разрыва при
значениях ![]() .
Величина
скачков =
.
Величина
скачков =![]() ;
; ![]() -
можно
рассматривать
как функцию распределения
дискретной
случайной
величины
-
можно
рассматривать
как функцию распределения
дискретной
случайной
величины ![]() с
вероятностью
с
вероятностью
![]() .
.
Подчеркнем,
что
выборочная
функция
распределения
![]() сама
является
дискретной
случайной
величиной,
которая
принимает
значения 0,
сама
является
дискретной
случайной
величиной,
которая
принимает
значения 0, ![]() ,
, ![]() ,…
,…![]() ,
, ![]() с
вероятностями
с
вероятностями
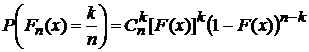 .
.
Поэтому
мы можем
говорить о
числовых
характеристиках
или
распределении
функции ![]() .
.
В
дальнейшем
будем
считать, что
выборка (1) располагается
в виде (2).
Разность
между наибольшим
и наименьшим
значениями
выборки называется
размахом
выборки.
Как
было указано
выше функцию ![]() можно
рассматривать
как функцию распределения
дискретной
случайной
величины
можно
рассматривать
как функцию распределения
дискретной
случайной
величины
|
|
|
|
… |
|
|
|
|
|
…. |
|
Для
этой
случайной
величины
можно вычислить
числовые
характеристики:
математическое
ожидание:
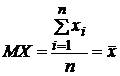 .
.
дисперсию:
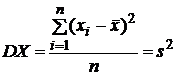 ,
,
для
которых
справедливы
все свойства
математического
ожидания и
дисперсии.
Для
![]() можно
получить
другое
выражение
можно
получить
другое
выражение
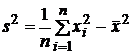
Величины
![]() и
и ![]() рассматриваются
в
математической
статистике в
качестве
оценок для
рассматриваются
в
математической
статистике в
качестве
оценок для ![]() и
и ![]() .
.
Аналогичным
образом
можно ввести
понятия
выборочных
моментов.
Определение.
Выборочным
моментом ![]() -го
порядка
называется
величина
-го
порядка
называется
величина 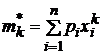 .
.
Отсюда
![]() ;
; ![]() -
выборочная
средняя.
-
выборочная
средняя.
Определение.
Центральным
выборочным
моментом
порядка ![]() называется
величина
называется
величина 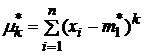 .
.
Отсюда
![]() ;
; ![]() ;
; ![]() -
выборочная
дисперсия.
-
выборочная
дисперсия.
Остальные
характеристики
(математическое
ожидание,
дисперсия,
моменты и т. д.)
получаются,
как
характеристики
этой
случайной величины.
А
именно
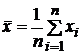 ,
, 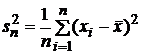 ,
,
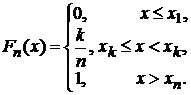
Для
характеристической
функции
выборки имеем
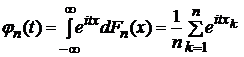 .
.
Аналогичные
характеристики
вводятся и
для
многомерных
распределений.
Например,
если имеется ![]() пар
значений
пар
значений ![]() , т. е.
выборку из
двумерного
распределения
, т. е.
выборку из
двумерного
распределения
![]() , то
, то
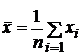 ,
,
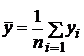 ,
,
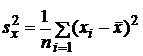 ,
,
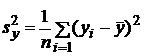 .
.
Коэффициент
регрессии
выборки
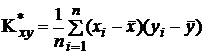 .
.
Коэффициент
корреляции
выборки
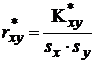 ,
,
![]() и
и ![]() может
принять свои
предельные
значения,
если все
выборочные
точки расположены
на одной
прямой.
может
принять свои
предельные
значения,
если все
выборочные
точки расположены
на одной
прямой.
Статистическим
аналогом
плотности
распределения
вероятностей
![]() является
гистограмма
частот или относительных
частот.
Гистограмма
строится
следующим
образом.
Подсчитываются
число
выборочных
значений
попавших в
каждый из
интервалов
некоторого
разбиения.
Каждый
интервал
этого
разбиения
берется в
качестве
основания
прямоугольника
высоты
является
гистограмма
частот или относительных
частот.
Гистограмма
строится
следующим
образом.
Подсчитываются
число
выборочных
значений
попавших в
каждый из
интервалов
некоторого
разбиения.
Каждый
интервал
этого
разбиения
берется в
качестве
основания
прямоугольника
высоты ![]() , где
, где ![]() -
длина
-
длина ![]() -го
интервала,
-го
интервала, ![]() -
число
выборочных
значений
попавших в
этот
интервал.
Получающаяся
фигура называется
гистограммой
выборки.
Площадь каждого
прямоугольника
равна
-
число
выборочных
значений
попавших в
этот
интервал.
Получающаяся
фигура называется
гистограммой
выборки.
Площадь каждого
прямоугольника
равна ![]() :
:
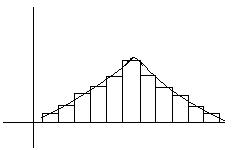
Гистограмма
выборки из
совокупности
с нормальной
функцией
распределения.
Отметим
следующее:
Каждая
характеристика
выборки ![]() может
рассматриваться,
как
наблюденное
значение
случайной
величины
может
рассматриваться,
как
наблюденное
значение
случайной
величины ![]() , где
, где ![]() независимые
величины,
имеющие то же
распределение,
что и
независимые
величины,
имеющие то же
распределение,
что и ![]() . Таким
образом, мы
можем
говорить о
распределении
случайной
величины
. Таким
образом, мы
можем
говорить о
распределении
случайной
величины ![]() , т. е. о
выборочном
распределении
среднего значения
, т. е. о
выборочном
распределении
среднего значения
![]() ,
дисперсии
,
дисперсии ![]() и
т. д.
и
т. д.
Так,
всякий раз,
когда мы
имеем дело с
выборочными
распределениями,
связанными с
данной совокупностью,
надо иметь в
виду, что
выборочные
характеристики
(![]() и т. д.)
рассматриваются
как
случайные
величины, в
то время, как
соответствующие
характеристики
генеральной
совокупности
(
и т. д.)
рассматриваются
как
случайные
величины, в
то время, как
соответствующие
характеристики
генеральной
совокупности
(![]() и т. д.)
фиксированные
(хотя иногда
и неизвестные)
постоянные.
и т. д.)
фиксированные
(хотя иногда
и неизвестные)
постоянные.