Тема 5. Интервальные оценки

1. Понятие доверительного интервала

2. Уровень значимости

Пусть необходимо оценить неизвестный параметр распределения .

Имеется выборка .

Пусть построена оценка для параметра . Значение оценки отличается, естественно, от значения параметра , т. е. – приближенная оценка. Значит необходимо указать границы погрешности этого приближения и тем самым надежность оценки .

В математической статистике этот вопрос решается путем определения таких величин и , чтобы интервал с заданной вероятностью содержал искомый параметр , т. е.

. (1)

Здесь ( - малая величина).

Величины и являются случайными величинами, значит и интервал является случайным.

Определение. Вероятность называется доверительной вероятностью или уровнем доверия; она определяет надежность выполнения неравенства

после вычисления и .

Определение. Интервал , удовлетворяющий условию (1), называется доверительным интервалом с заданным уровнем доверия . Величина называется уровнем значимости.

Иногда определяют симметричный интервал

.

Практически поступают следующим образом: по выборке , полученной для величины с функцией распределения , находят значения доверительного интервала с уровнем доверия и считают, что истинное значение параметра с надежностью попадает в этот интервал. Так как при конкретной выборке величины и не являются случайными величинами, то здесь уже не говорят о вероятности.

Рассмотрим общий подход для определения доверительного интервала. По данной выборке надо построить такую монотонную по функцию с известным распределением, что для нее можно разрешить относительно неравенство

.

Решение этого неравенства дает и , которые и определяют доверительный интервал с заданным уровнем доверия, равным вероятности исходного неравенства. При этом можно варьировать и так, чтобы получить наиболее узкий интервал:

.

Пример. Построим доверительный интервал для математического ожидания нормально распределенной случайной величины при известном .

Пусть имеется выборка для нормально распределенной случайной величины с параметрами . Обозначим: .

Случайная величина 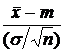(где 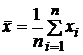) распределенная нормально с параметрами (0,1), т. е. . Таким образом, в качестве функции используется функция .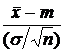

Для всякого можно найти такое , что

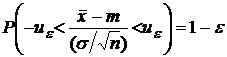. (2)

Здесь использован симметричный интервал, потому что для при заданном он минимален. Выражение (2) можно переписать так:

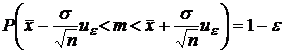(3)

Неравенство

определяет доверительный интервал для неизвестного параметра с уровнем доверия или доверительной вероятностью .

Как определить ?

Выражение (3) равносильно

.

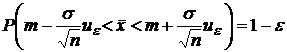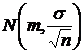Так как распределен нормально с параметрами и , т. е. , то

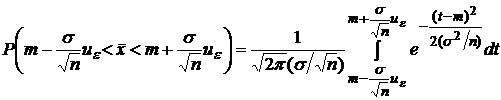
Делая замену 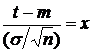и учитывая (3) получим, что

.

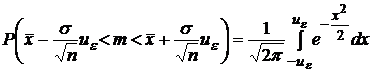Таким образом, для определения получаем:

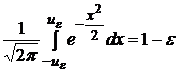. (4)

Существуют таблицы интегралов, с помощью которых и находят при заданном значение . Они составлены для функции Лапласа

.

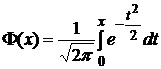Интеграл в (4) можно написать в следующем виде

.

Отсюда . Используя таблицы, находим .