Тема
4. Методы
нахождения
оценок
неизвестных
параметров
распределения
2.
Метод
максимального
правдоподобия
Пусть
![]() -
случайная
величина.
Закон
распределения
задан
плотностью
-
случайная
величина.
Закон
распределения
задан
плотностью ![]() ;
; ![]() -
неизвестно.
-
неизвестно.
Определение.
Среднее
значение
функции ![]() (если
(если ![]() интегрируема
на
интегрируема
на ![]() )
относительно
)
относительно
![]() называется
моментом
порядка
называется
моментом
порядка ![]() случайной
величины
случайной
величины ![]() с
функцией
распределения
с
функцией
распределения
![]() :
:
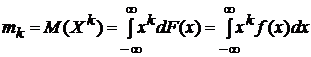 ,
,
где
![]() -
плотность
распределения
вероятностей.
-
плотность
распределения
вероятностей.
Для
дискретной
случайной
величины
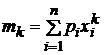 ,
,
![]() -
всегда
существует,
-
всегда
существует,
![]() -
математическое
ожидание
случайной
величины.
-
математическое
ожидание
случайной
величины.
Определение.
Центральным
моментом
порядка ![]() называется
величина
называется
величина
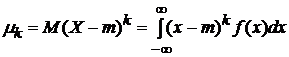 ,
где
,
где ![]() ;
;
![]() ,
,
![]() ,
,
![]() -
дисперсия
случайной
величины.
-
дисперсия
случайной
величины.
Метод
моментов
состоит в
следующем:
по
выборке ![]() строят
выборочные
моменты
строят
выборочные
моменты
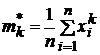
или
центральные
выборочные
моменты
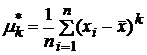 ,
где
,
где 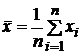 .
.
Затем
определенное
количество
этих моментов
приравнивают
к соответствующим
моментам ![]() или
или ![]() распределения
распределения
![]() , которые
являются
функциями
неизвестных параметров
(или
параметра).
, которые
являются
функциями
неизвестных параметров
(или
параметра).
Рассматривая
количество
моментов,
равное числу
неизвестных
параметров,
подлежащих
оценке, и
решая
полученную
таким образом
систему
относительно
этих
параметров, мы
получим
соответствующие
оценки.
Пример
1.
Пусть
необходимо
оценить
неизвестную вероятность
события ![]() .
.
С
событием ![]() можно
связать
случайную
величину
можно
связать
случайную
величину ![]() следующего
вида
следующего
вида
|
|
1 |
0 |
|
|
|
|
(1)
т.
е. ![]() =1, когда
событие
=1, когда
событие ![]() наступает
и
наступает
и ![]() =0 в
противном
случае.
=0 в
противном
случае.
Таким
образом,
имеем
распределение
(2.4.1) с
неизвестным
параметров ![]() .
.
Пусть
имеем
выборку ![]() , т. е.
проводим
, т. е.
проводим ![]() раз
эксперимент
раз
эксперимент ![]() , при
котором
событие
, при
котором
событие ![]() наступает
или нет.
наступает
или нет.
По
выборке
строим
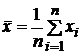 .
.
Из
распределения
(1) находим 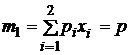 .
.
Приравниваем
![]() . Таким
образом,
оценкой для
. Таким
образом,
оценкой для ![]() будет
будет
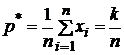 (статистическое
определение
вероятности)
(статистическое
определение
вероятности)
Метод
максимального
правдоподобия.
Пусть
![]() -
случайная
величина,
закон
распределения
которой
задан
плотностью
-
случайная
величина,
закон
распределения
которой
задан
плотностью ![]() ;
; ![]() -
неизвестный
параметр.
-
неизвестный
параметр.
Функция
![]() (2)
(2)
является
при
фиксированном
![]() плотностью
вероятности выборки
плотностью
вероятности выборки
![]() ; при
фиксированной
выборке ее
можно рассматривать,
как функцию
параметра
; при
фиксированной
выборке ее
можно рассматривать,
как функцию
параметра ![]() . В
последнем
случае будем
называть (2) функцией
правдоподобия.
. В
последнем
случае будем
называть (2) функцией
правдоподобия.
Суть
метода
максимального
правдоподобия
состоит в
том, что в
качестве
оценки параметра
![]() берется
такое
значение
берется
такое
значение ![]() , при
котором
, при
котором ![]() достигает
наибольшего
возможного
значения. Так
как
достигает
наибольшего
возможного
значения. Так
как ![]() достигает
максимума
при том же
значении
достигает
максимума
при том же
значении ![]() , что и
сама
, что и
сама ![]() , то на
практике
часто
удобнее
использовать
функцию
, то на
практике
часто
удобнее
использовать
функцию ![]() , которую
можно называть
логарифмической
функцией
правдоподобия.
, которую
можно называть
логарифмической
функцией
правдоподобия.
Значение
![]() является
функцией
выборки
является
функцией
выборки ![]() и
называется оценкой
максимального
правдоподобия.
и
называется оценкой
максимального
правдоподобия.
Для
нахождения
оценки
максимального
правдоподобия
![]() решается
относительно
решается
относительно![]() уравнение
уравнение
![]() .
(3)
.
(3)
Для
случая
нескольких
неизвестных
параметров
или выборки
из
многомерного
распределения
метод
максимального
правдоподобия
формулируется
как и выше.
Так,
например, для
непрерывного
распределения
с двумя
неизвестными
параметрами ![]() и
и ![]() функций
правдоподобия
будет
функций
правдоподобия
будет
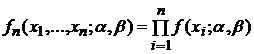 .
.
Оценки
максимального
правдоподобия
для ![]() и
и ![]() получаются
из решения
системы уравнений
получаются
из решения
системы уравнений
![]() ,
, 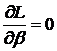 ,
,
где
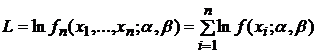 .
.
Дискретный
случай
|
|
|
|
… |
|
|
|
|
|
… |
|
|
|
|
|
… |
|
,
![]() -
зависят от
неизвестного
параметра
-
зависят от
неизвестного
параметра ![]() .
.
Функция
правдоподобия
имеет вид
![]() ,
,
где ![]() -
частота
значений
-
частота
значений ![]() в
выборке
в
выборке ![]() , при этом
, при этом 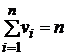 ,
, ![]() -
называются вариантами.
-
называются вариантами.
Пример
2.
Для выборки в
![]() значений
из
нормального
распределения
с
неизвестными
параметрами
значений
из
нормального
распределения
с
неизвестными
параметрами ![]() и
и ![]() :
:
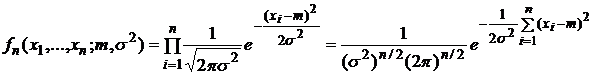 .
.
Логарифмическая
функция
правдоподобия
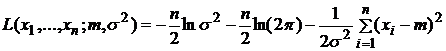 .
.
Метод
максимального
правдоподобия
приводит к
уравнениям:
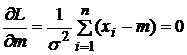 ,
,
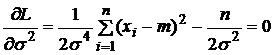 .
.
Откуда
получаем
оценки
максимального
правдоподобия
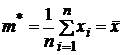
и 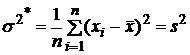 .
.
Пример
3.
Найдем
оценку
неизвестной
вероятности
события ![]() из
условия
примера 1
методом
максимального
правдоподобия.
из
условия
примера 1
методом
максимального
правдоподобия.
Функция
правдоподобия
в этом случае
при ![]() ,
, ![]() и
и ![]() ,
, ![]() имеет
вид:
имеет
вид:
![]() ,
,
![]() .
.
Составим
уравнение
правдоподобия:
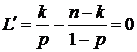 .
.
Решением
этого
уравнения
является
оценка для
неизвестной
вероятности ![]() .
.
![]() .
.