Тема
3. Неравенство
Рао-Крамера
Пусть
![]() выборка
из
генеральной
совокупности
выборка
из
генеральной
совокупности
![]() ;
; ![]() -
случайная
величина с
плотностью распределения
-
случайная
величина с
плотностью распределения
![]() , где
, где ![]() неизвестный
параметр
распределения.
неизвестный
параметр
распределения.
Рассмотрим
функцию
![]() ,
,
которая
при
фиксированном
![]() представляет
собой
плотность
распределения
вероятности
выборки
представляет
собой
плотность
распределения
вероятности
выборки ![]() . Если
. Если ![]() -
случайный
вектор, то
-
случайный
вектор, то ![]() -
случайная
величина,
зависящая от
параметра
-
случайная
величина,
зависящая от
параметра ![]() .
.
Введем
также
функцию
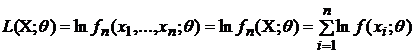 .
.
Пусть
функция ![]() -
оценка
параметра
-
оценка
параметра ![]() , причем
, причем ![]() ,где
,где
![]() -
смещение
оценки
-
смещение
оценки ![]() .
Выразим
.
Выразим ![]() через
через ![]() :
:
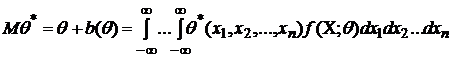 . (1)
. (1)
Известно,
что
![]() ,
(
,
(![]() ).
(2)
).
(2)
Продифференцируем
(1) по ![]() (используя
дополнительно
условие, что
производную
по
(используя
дополнительно
условие, что
производную
по ![]() можно
вносить под
знак
интеграла).
можно
вносить под
знак
интеграла).
Получим
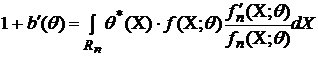 . (3)
. (3)
Так
как
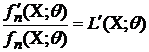 ,
,
то
из (3) имеем:
![]() . (4)
. (4)
Продифференцируем
по ![]() выражение
(2):
выражение
(2):
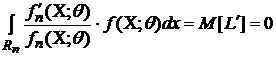 . (5)
. (5)
Обозначим
![]() .
.
Умножим
выражение (5)
на ![]() и
вычтем из (4):
и
вычтем из (4):
![]()
или
![]() . (6)
. (6)
Правая
часть (6)
представляет
собой
квадрат ковариации
между
величинами ![]() и
и ![]() , т. е.
, т. е. ![]() , так как
, так как ![]() .
.
Коэффициент
корреляции
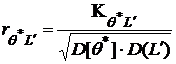 ,
,
и
так как ![]() , (т.е.
, (т.е. ![]() ),
),
то
![]()
или
![]() .
.
Отсюда
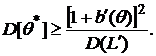 (7)
(7)
Полученное
выражение
называется неравенством
Рао-Крамера.
Здесь
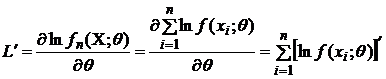 .
.
Таким
образом, ![]() -
представляет
собой сумму
одинаково
распределенных
независимых
случайных
величин
-
представляет
собой сумму
одинаково
распределенных
независимых
случайных
величин
![]() ,
,
причем
согласно (5), ![]() .
.
Значит
![]() . (8)
. (8)
Используя
(8), имеем
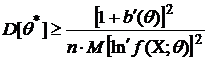 .
.
Если
оценка ![]() является
несмещенной,
т. е.
является
несмещенной,
т. е. ![]() , то
, то
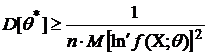 .
.
Еще
раз отметим,
что мы
предполагали,
что плотность
![]() допускает
дифференцирование
по
допускает
дифференцирование
по ![]() выражений
(1) и (2) под
знаком
интеграла.
выражений
(1) и (2) под
знаком
интеграла.
Справедлива
также теорема:
В классе
несмещенных
оценок
эффективная оценка
единственна.
Пример.
Проверить:
является или
нет ![]() эффективной
оценкой для
математического
ожидания
нормально
распределенной
случайной
величины
эффективной
оценкой для
математического
ожидания
нормально
распределенной
случайной
величины ![]() .
.
Решение.
Пусть имеем ![]() -
выборку из
-
выборку из ![]() , где
параметр
, где
параметр ![]() -
неизвестен.
-
неизвестен.
Оценкой
для ![]() является
является
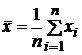 .Найдем
.Найдем
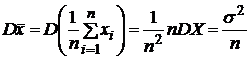 .
.
Найдем
правую часть
неравенства
Рао-Крамера:
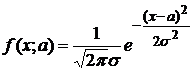 ,
,
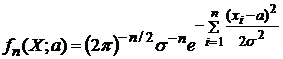 ;
;
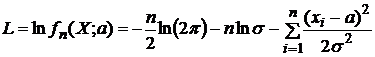 ,
,
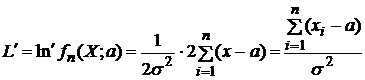 ,
,
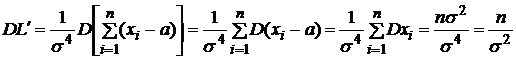 ,
,
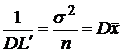 .
.
Таким
образом ![]() является
эффективной
оценкой для параметра
является
эффективной
оценкой для параметра
![]() .
.