Лекция 11. Кратный предел функции многих переменных. Повторные пределы функции. Вычисление.

При изучении многих вопросов естествознания встречаются такие зависимости между несколькими переменными величинами, когда значения одной из этих переменных величин полностью определяются значениями остальных переменных. Так, при рассмотрении каких-либо физических характеристик тела (например, его плотности или температуры) нам приходится учитывать изменение этих характеристик при переходе от одной точки тела к другой. Поскольку каждая точка тела определяется тремя декартовыми координатами и , то рассматриваемые характеристики определяются значениями трех переменных и .

При рассмотрении физических процессов, меняющихся во времени, значения физических характеристик определяются значениями четырех переменных: и времени . Например, при изучении звуковых колебаний газа плотность этого газа и давление определяются значениями четырех переменных и . При изучении такого рода зависимостей введем понятие функции нескольких переменных.

Как известно, функцией называется соответствие между двумя множествами и любой природы, по которой каждому элементу ставится в соответствие определенный . При этом множество называется областью определения этой функции. Если область определения является подмножеством пространства , а множество является подмножеством числовой оси , то такая функция называется числовой функцией переменных.

Если координаты точек считать значениями некоторых переменных , а множество считать значениями другой переменной , то функция - переменных обозначается следующим образом: , - означает закон или правило соответствия. В случае функций 2-х переменных будет использоваться также обозначение , а в случае трех переменных . Графически можно изобразить лишь функции одного или двух аргументов. Графиком функции называется поверхность, точки которых имеют координаты . Рассмотрим примеры функций двух переменных.

1. . Областью определения этой функции является круг радиуса 2 с центром в начале координат, а множество значений представляет собой сегмент .

2. . Областью определения этой функции является множество точек, лежащих вне круга радиуса 2 с центром в начале координат, а множество значений представляет собой полуось .

Примеры: Найти область определения функции:

1) . По определению арккосинуса модуль его аргумента должен быть меньше и равен единице. Поэтому потребуем, чтобы выполнялось неравенство:

. Ответ.

2) . Аргумент логарифмической функции должен быть строго положительным. Поэтому потребуем выполнения неравенства

а) . Рис.

б) . Рис.

Ответ. .

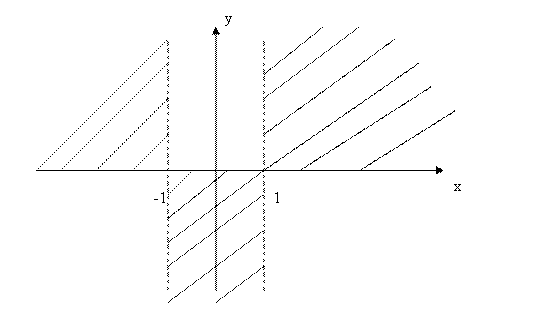
Рассмотрим функцию , определенную на некотором множестве и точку этого множества, может быть, и не принадлежащую этому множеству, но обладающую тем свойством, что в любой - окрестности этой точки содержится хотя бы одна точка множества , отличная от .

Определение 1. Число называется предельным значением функции в точке (или пределом функции при ), если для любой сходящейся к последовательности множества , элементы которой отличны от , соответствующая последовательность значений функций сходится к .

Данное определение называется определением предельного значения функции с помощью последовательностей. Теперь сформулируем это определение, используя «» терминологию.

Определение 2. Число называется предельным значением функции в точке , если для любого положительного числа можно указать такое положительное число , что для всех точек из области задания функции, удовлетворяющих условию

выполняется неравенство .

Записывается это так:

Сформулируем определение предельного значения функции при стремлении точки к бесконечности.

Такой предел называется также кратным пределом функции в точке . В случае 2-х аргументов, т.е. когда кратный предел называется двойным пределом.

Эквивалентным определением предела является

/ ,

. (2)

Как и в случае одной переменной и точка могут быть бесконечностями.

Арифметические операции над функциями переменных, имеющими предельное значение в точке , приводят к функциям, также имеющим предельное значение в точке . Справедливо следующее утверждение.

Утверждение. Пусть функции и имеют в точке предельные значения и . Тогда функции +, -, и имеют в точке предельные значения (частное при условии ), равные соответственно , , , .

Будем говорить, что функция удовлетворяет в точке условию Коши если для любого положительного числа найдется положительное число такое, что каковы бы ни были две точки и из области определения функции, удовлетворяющие неравенствам , , для соответствующих значений функций справедливо неравенство .

Теорема (критерий Коши). Для того чтобы функция имела конечное предельное значение в точке , необходимо и достаточно, чтобы функция удовлетворяла условию Коши.

Доказательство. 1) необходимость. Пусть существует конечное предельное значение . Докажем, что функция удовлетворяет в точке условию Коши. Возьмем произвольное . Согласно определению предельного значения функции для положительного числа найдется положительное число такое, что каковы бы ни были значения аргумента и , удовлетворяющие неравенствам

, , для соответствующих значений функции справедливы неравенства , . Так как модуль суммы двух величин не превосходит суммы их модулей, то из последних неравенств получим

Тем самым доказано, что функция удовлетворяет в точке условию Коши.

2) достаточность. Пусть функция удовлетворяет в точке условию Коши. Докажем, что функция имеет предельное значение в точке . Пусть - любая сходящаяся к последовательность аргумента, все элементы которой отличны от . В силу предельного значения функции достаточно доказать, что соответствующая последовательность значений функций сходится к некоторому числу , причем это число одно и то же для всех сходящихся к последовательностей таких, что .

Докажем сначала сходимость любой последовательности . Пусть задано произвольное . Возьмем то положительное число , которое соответствует этому согласно условию Коши, и, пользуясь сходимостью последовательности к , выберем для этого номер такой, что

при .

При этом для любого натурального и подавно

при .

Последние два неравенства в силу условия Коши приводят к неравенству при , т.е. доказывают фундаментальность последовательности . В силу критерия Коши для последовательности последовательность сходится к некоторому числу .

Докажем теперь, что все последовательности , соответствующие всевозможным сходящимся к последовательностям , имеют один и тот же предел .

Пусть и - любые две сходящиеся к последовательности значений аргумента, все элементы которых отличны от . В силу доказанного выше обе последовательности и сходятся. Обозначим предел первой из этих последовательностей через , а второй – через . Докажем, что . Рассмотрим сходящуюся к последовательность

.

В силу доказанного выше, соответствующая последовательность значений функции

является сходящейся. Но тогда все подпоследовательности, в том числе и , сходятся к одному и тому же пределу, т.е. . Ч.т.д.

Рассмотрим основные свойства конечного предела функций многих переменных:

1. Если функция имеет конечный предел в данной точке по множеству , то сама функция ограничена в некоторой проколотой окрестности точки , точнее существует и существует .

2. Если функция имеет конечный предел в данной точке по множеству , то этот предел единственный.

3. Для того, чтобы существовал конечный предел , необходимо и достаточно, чтобы функцию можно представить в виде суммы числа и некоторой бесконечно малой функции в окрестности точки , т.е, чтобы выполнялось равенство:

, .

4. Если существуют конечные пределы

и , то существуют пределы разности, суммы и произведения этих функций, а также предел отношения, если не равны нулю, причем выполняются равенства

;

.

4. Пусть внутренние функции имеют пределы:

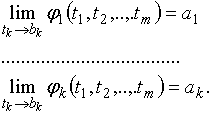
Внешняя функция также имеет предел:

, то в случае существования сложной функции она также имеет предел

.

При прохождении кратных пределов часто применяют следующие свойства б.б. и б.м. функций.

a) сумма любого конечного фиксированного числа б.м. функций сама является б.м. функцией в данной точке;

b) произведение б.м. функции на ограниченную функцию является некоторой б.м. функцией в данной точке; значит, произведение б.м. функции также является б.м. функцией (потому что любая б.м.функция является ограниченной);

c) если функция является б.м. и отлична от нуля в некоторой окрестности точки . Верно и обратное утверждение;

d) Сумма ограниченной функции и б.б. функции является б.б. функцией. Однако сумма (разность) двух б.б. функций может не быть б.б., в этом случае возможна неопределенность вида . Если же область слагаемых является б.б. функцией одного и того же знака, то сумма также является б.б. того же знака. Возможны и другие случаи бесконечности предела суммы.

Пример 1. Найти предел функции

.

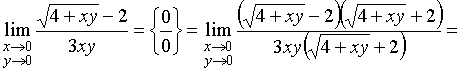
Пример 2. Найти предел функции

.