ЛЕКЦИЯ 8. ГРАФИКИ УРАВНЕНИЙ. ПРЕОБРАЗОВАНИЕ ГРАФИКОВ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ.

План лекции:

1) Графическое изображение кривых, задаваемых уравнением.

2) Сложение, умножение и другие преобразования графиков элементарных функций.

Графиком функции, заданной уравнением , надо найти совокупность всех точек плоскости, координаты которых удовлетворяют этому уравнению.

Обычно график функции представляет некоторую плоскостную линию.

Построение графика аналитически заданной функции по точкам выполняется в следующе порядке:

1) по данному аналитическому выражению функции составляется таблица соответствующих друг другу значений переменных;

2) выбирается система координат с подходящими единицами масштаба для каждой переменной (обычно выбирается прямоугольная декартовая система координат с одинаковым масштабом на каждой оси);

3) строятся точки, координатами которых являются соответствующие друг другу значения аргумента и функций, содержащиеся в таблице;

4) полученные точки соединяют плавной линией.

Чтобы построить график функции , надо построить на одном чертеже графики функций и , потом при каждом сложить ординаты функций.

Пример. Построить график функции .

y

Решение. Построим графики функций (голубая прямая) и (зеленая кривая) на одном чертеже.

x

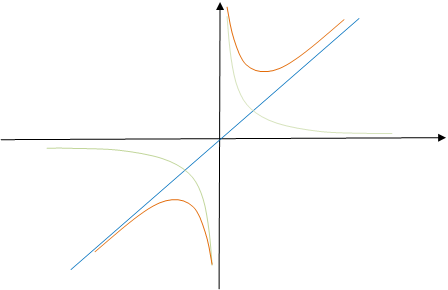
Графиком функции является оранжевая кривая.

Если необходимо построить график функции , то этот случай сводится к построению суммы , причем график функции , полученный из графика функции , симметрично отображен относительно оси .

В случае, когда вторая функция постоянна, то график сложения определяется сдвигом графика первой функции по вертикали на эту постоянную вверх, если она положительна и вниз, если она отрицательна.

Чтобы построить график функции , надо построить на одном чертеже графики и и при каждом значении аргумента перемножить ординаты этих двух графиков.

Пример. Построить график функции .

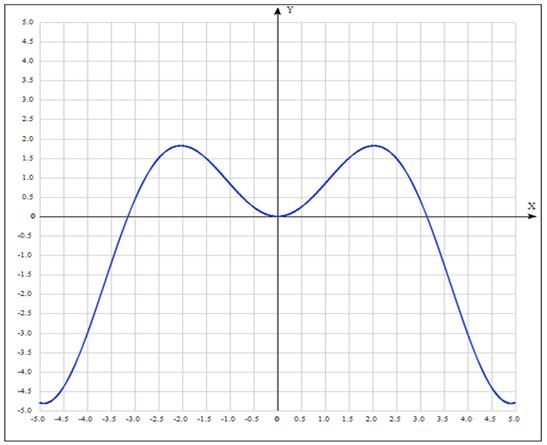
График функции получается из графика функции сдвигом вдоль оси на единиц. Направление сдвига определяется знаком числа (при график сдвигается вверх, при вниз).

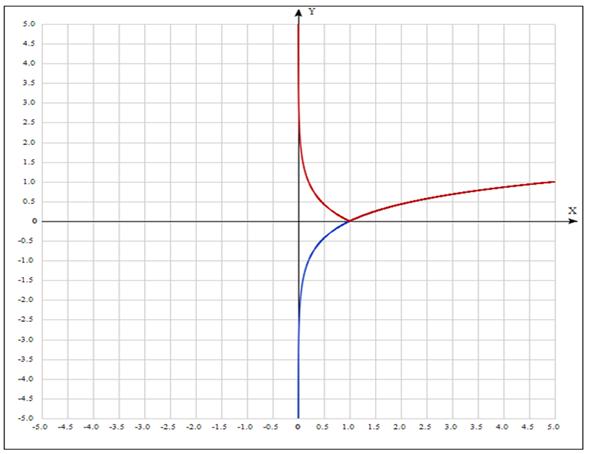
Пример. Построить график функции .

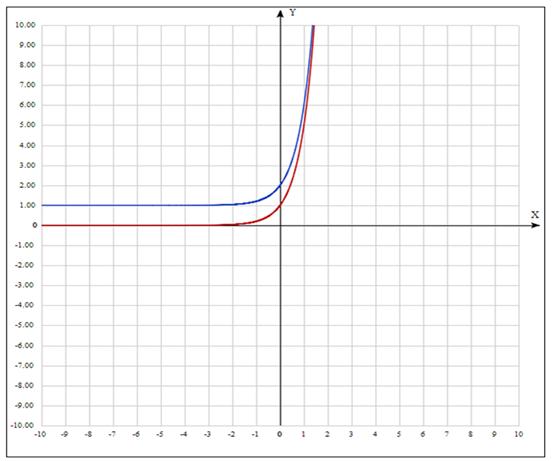
1. - красный

2. - синий.

График функции получается из графика функции сдвигом вдоль оси на единиц. Направление сдвига определяется знаком числа (при график сдвигается влево, при вправо).

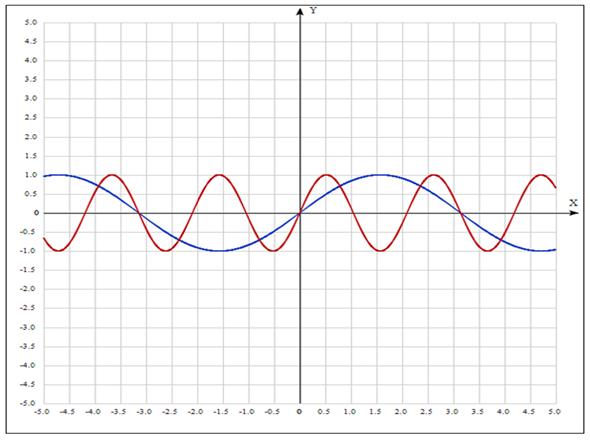
Пример. Построить график функции .

1. - красный

2. - синий

Чтобы из графика функции получить график функции , где , надо произвести сжатие графика функции вдоль оси абсцисс в раз. В случае надо произвести растяжение графика функции вдоль оси абсцисс в раз. Если , то надо построить график функции и зеркально отобразить относительно оси .

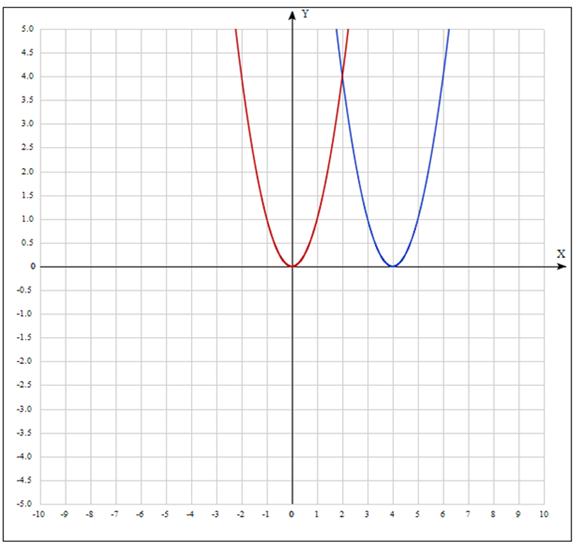
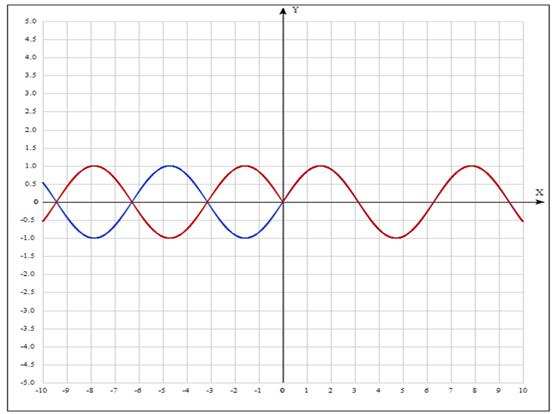
Пример. Построить график функции .

1. - синий

2. - красный

Чтобы из графика функции получить график функции , где , надо растянуть график функции в раз вдоль оси абсцисс в раз. В случае надо произвести растяжение графика функции вдоль оси ординат, если и сжать в раз вдоль оси ординат, если

Пример. Построить график функции .

1. - синий

2. - красный

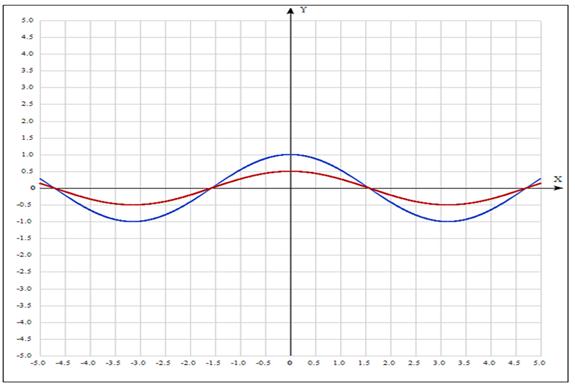
Чтобы из графика функции получить график , нужно участки графика , лежащие выше оси абсцисс, оставить без изменения, а участки, лежащие ниже оси абсцисс, отразить симметрично относительно этой оси.

Пример. Построить график функции .

- красный

Чтобы из графика функции получить график , надо правую половину графика , () оставить без изменения, а левую половину заменить на симметричное отражение относительно этой правой половины.

Пример. Построить график функции .

- красного цвета

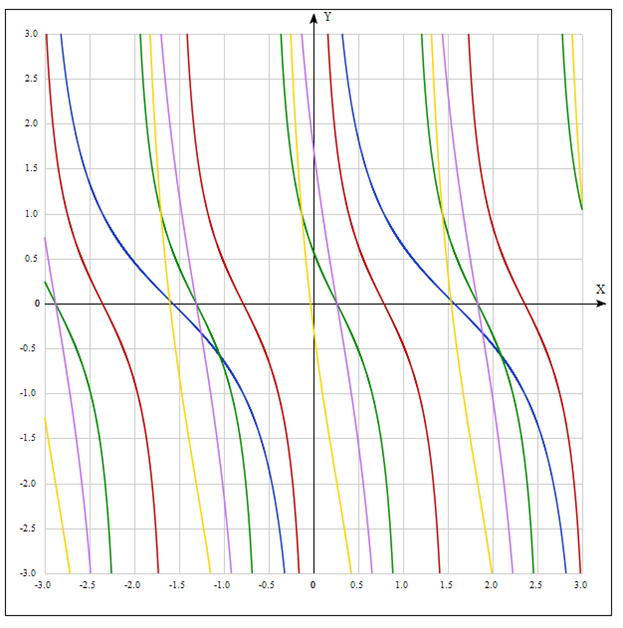
Пример. Построить график функции .

1. - синий

2. - красный

3. - зеленый

4. - розовый

5. Искомый график - желтого цвета