Министерство образования и науки РФ

Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования

«Дагестанский государственный университет»

Физический факультет

Методическое пособие

к выполнению лабораторных работ по курсу

«Материалы электронной техники»

Автор:

доцент каф.ЭФ, к.ф.-м.н.

Офицерова Н.В.

Махачкала 2017

Содержание.

1. Лабораторная работа №1. Определение ширины запрещенной зоны полупроводника.

2. Лабораторная работа №2. Исследование электропроводности металлов.

3. Лабораторная работа №3. Определение концентрации и холловской подвижности основных носителей заряда.

4. Лабораторная работа №4. Исследование электропроводности тугоплавких металлов и сплавов высокого сопротивления.

5. Лабораторная работа №5. Исследование сегнетоэлектриков.

6. Лабораторная работа №6. Исследование диэлектрической проницаемости и диэлектрических потерь в твердых диэлектриках.

7. Лабораторная работа №7. Исследование влияния магнитного поля на удельное сопротивление полупроводника.

Лабораторная работа №1

Определение ширины запрещенной зоны полупроводника.

Цель работы: определение ширины запрещенной зоны германия, используя температурную зависимость электропроводности.

Теория

Порядок выполнения работы

Контрольные вопросы

Литература

Теория

Удельная электропроводность твердого тела зависит от концентрации носителей заряда, их подвижности и определяется по формуле:

(1)

где e – заряд, n – концентрация свободных носителей заряда, m - подвижность носителей заряда.

Собственный полупроводник. Собственная проводимость

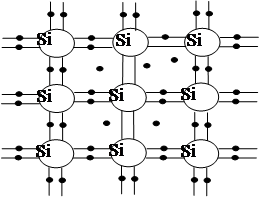
Рассмотрим механизм проводимости собственного полупроводника на примере классических полупроводников Ge, Si – 4 – ой группы таблицы Д.И. Менделеева, валентность – 4, каждый атом Si и Ge образуют парноэлектронную связь с 4 – мя ближайшими соседями. Вид этих связей в плоскости показан на рис.1а. В узле решетки находится атомный остаток с зарядом +4, заряд которого компенсируется четырьмя валентными электронами, участвующими в связях.

В электрическом поле в таком полупроводнике ток не возникает, так как нет свободных электронов. Если под действием каких - либо внешних факторов происходит разрыв валентной связи, т.е. отрыв электрона от атома, то возникает свободный электрон, а в месте разрыва валентной связи образуется положительный заряд. Этот положительный заряд или ненасыщенная валентная связь получила название дырки. Таким образом, при ионизации атомов решетки образуются свободные электроны и свободные дырки. На зонной диаграмме это означает переход электрона из валентной зоны в зону проводимости (рис.1б). Отметим, что свободны только электроны, перешедшие в зону проводимости и дырки в валентной зоне. В таком кристалле число свободных электронов равно числу свободных дырок.

Полупроводник, в котором свободные носители заряда образуются за счет ионизации атомов решетки или разрыва валентных связей называется собственным, а электропроводность, обусловленная ими, называется собственной электропроводностью. Во внешнем электрическом поле будут двигаться свободные электроны и дырки. Электроны будут двигаться против поля, а дырки по направлению поля. Электропроводность, обусловленная движением дырок, называется дырочной проводимостью. Следовательно, электрический ток в собственном полупроводнике определяется двумя составляющими – электронным и дырочным токами. Суммарная электропроводность равна:

(2)

где p и m_p концентрация и подвижность дырок, соответственно.

Так как в собственном полупроводнике концентрации электронов и дырок равны, то

(3)

где i – индекс собственной проводимости.

Энергия ионизации атомов решетки равна ширине запрещенной зоны. Для Ge она составляет 0,66 эВ, для Si– 1,12 эВ.

а) б)

Рис.1. Схематическое изображение кристаллической решетки (а) и зонная энергетическая диаграмма (б) собственного полупроводника.

а) б)

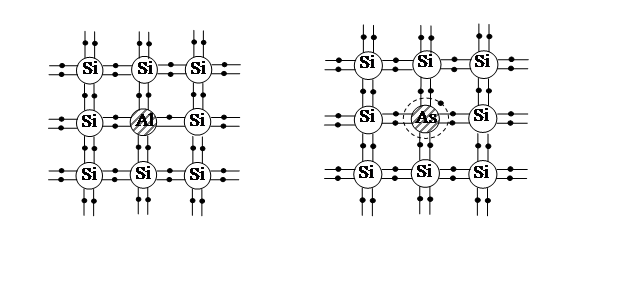
Рис.2. Схематическое изображение кристаллической решетки акцепторного (а) и донорного (б) полупроводников.

Примесный полупроводник. Примесная проводимость

Наряду с собственными полупроводниками имеется широкий класс полупроводников, в котором концентрация носителей заряда определяется примесями. Такие полупроводники называются примесными.

Рассмотрим механизм образования свободных электронов и дырок в примесном полупроводнике. Рассмотрим конкретный случай. В решетку Siвведена примесь V группы – атомы мышьяка, и пусть атомы мышьяка замещают в решетке атомы кремния. Мышьяк имеет 5 валентных электронов, 4 из них устанавливают связи с атомами Si. Пятый электрон не участвует в установлении связей, и, поэтому, слабо связан с атомом мышьяка. Слабосвязанный электрон вращается вокруг иона мышьяка, образуя водородоподобную систему (рис.2б). При повышении температуры этот электрон легко отрывается от атома мышьяка и свободно перемещается по кристаллу. Электрон переходит в зону проводимости. В результате образуется свободный электрон и положительный ион мышьяка – связанная дырка. Эта дырка не может свободно перемещаться по кристаллу, т.к. отсутствует ненасыщенная связь. Энергия ионизации атома мышьяка гораздо меньше энергии ионизации атомов решетки – кремния, поэтому на зонной диаграмме уровни энергии атомов примеси будут расположены около дна зоны проводимости. В таком полупроводнике основными носителями заряда будут электроны, и полупроводник называется электронным или n – типа полупроводником. Сама примесь, отдающая электроны, называется донорной примесью; уровни энергии этой примеси на зонной диаграмме – донорными уровнями. Энергия ионизации донорной примеси равна

(4)

где E_c – энергетическое положение дна зоны проводимости; E_d – энергетическое положение атомов примеси.

Если в решетку кремния внедрены атомы третьей группы с тремя валентными электронами, например, Al, то для насыщения валентных связей кристаллической решетки не хватает одного электрона. Эта ненасыщенная связь, локализованная около атома алюминия, будет вести себя как дырка. Она может быть насыщена путем разрыва валентной связи основного атома решетки и захвата электрона разорвавшейся связи (ри.2а). В результате образуется свободная дырка и, связанный на атоме алюминия, электрон, т.е. отрицательно заряженный ион алюминия. В проводимости кристалла участие принимает только свободная дырка. Примесь, захватывающая электрон называется акцепторной, а полупроводник дырочным или p – типа, т.к. основными носителями заряда являются дырки. На зонной диаграмме это означает переход электрона из валентной зоны на уровень примеси, расположенный в этом случае около потолка валентной зоны.

Энергия ионизации акцепторной примесь гораздо меньше энергии ионизации атомов основного вещества и равна

(5)

где E_a – энергетическое положение атомов примеси; E_v – энергетическое положение потолка валентной зоны.

Таким образом, для ионизации атомов решетки и примеси и образования свободных носителей заряда в собственном и примесном полупроводнике необходимо затратить энергию. Поэтому концентрация носителей заряда в полупроводнике зависит от температуры. При абсолютном нуле температуры свободные носители заряда отсутствуют и зона проводимости пуста. С ростом температуры тепловая энергия атомов растет и начинается процесс ионизации. 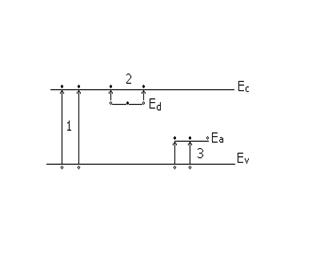Поскольку энергия ионизации примеси меньше, чем ширина запрещенной зоны, то при низких температурах происходит в основном ионизация примесных атомов (переходы 2,3 , рис.1б) и полупроводник будет иметь примесную проводимость. С ростом температуры начинается ионизация атомов решетки, и будут осуществляться переходы электронов из валентной зоны в зону проводимости. При этом образуются свободные электроны и дырки. Полупроводник обладает теперь собственной проводимостью. Тип проводимости и в собственном полупроводнике определяется типом примеси, т.к. в донорном полупроводнике концентрация электронов будет больше концентрации дырок, а в акцепторном наоборот.

Температурная зависимость электропроводности

Чтобы найти зависимость электропроводности от температуры, нужно найти температурную зависимость концентрации носителей заряда и их подвижности от температуры.

Концентрация электронов в зоне проводимости определяется как

(6)

где N(E) – плотность квантовых состояний в интервале энергий от Eдо E + dE; f(E,T) – вероятность их заполнения.

Вероятность того, что состояние с энергией Е занято электроном определяется распределением Ферми – Дирака

(7)

где E_F –уровень Ферми, k– постоянная Больцмана, Т - температура.

Плотность квантовых состояний определяется как

(8)

гдеh – постоянная Планка, - эффективная масса электрона.

Подставив (7) и (8) в (6) получим для концентрации электронов и дырок в полупроводнике

(9)

(10)

где N_c, N_v– эффективные плотности квантовых состояний в зоне проводимости и валентной зоне, соответственно.

Для собственного полупроводника , тогда умножив (9) на (10), получим

(11)

где + - ширина запрещенной зоны.

Из формулы (11) видно, что концентрация носителей заряда в собственном полупроводнике зависит от температуры и ширина запрещенной зоны.

Подвижность носителей заряда – это дрейфовая скорость, приобретаемая электроном в электрическом поле единичной напряженности. Единица измерения подвижности м²/В с. Величина подвижности и ее температурная зависимость определяется механизмом рассеяния носителей заряда. При рассеянии носителей заряда на тепловых колебаниях решетки (этот механизм рассеяния имеет место в ковалентных кристаллах типа Ge, Si) подвижность . С ростом температуры подвижность падает, т.к. увеличиваются тепловые колебания атомов и соответственно, рассеяние носителей заряда на них.

Таким образом, температурная зависимость электропроводности определяется температурной зависимостью концентрации носителей заряда и их подвижностью. Однако, концентрация носителей заряда от температуры зависит по сильному экспоненциальному закону, а подвижность – по сравнительно слабому степенному закону. Поэтому температурный ход электропроводности как примесного, так и собственного полупроводников определяется температурной зависимостью концентрации носителей заряда в нем. Электропроводность полупроводника, в котором имеются примеси, выражается формулой

(12)

Здесь первое слагаемое - величина собственной электропроводности, второе – величина примесной электропроводности.

График этой зависимости изображается в полулогарифмических координатах

(13)

На рис.3 приведен примерный график зависимости концентрации носителей заряда и электропроводности от температуры. На участке аб при низких температурах с ростом температуры концентрация носителей заряда и, соответственно, электропроводность растет с температурой за счет ионизации донорных примесей и перехода электронов с донорных уровней в зону проводимости. При температуре Т_s все донорные примеси ионизированы, а тепловая энергия еще недостаточна для ионизации атомов решетки, поэтому на участке бв концентрация носителей заряда не меняется, а электропроводность уменьшается в результате зависимости подвижности от температуры. На участке вг электропроводность увеличивается за счет ионизации атомов решетки. Резкое возрастание собственной электропроводности объясняется высокой концентрацией атомов решетки по сравнению с концентрацией атомов примеси.

Из температурной зависимости электропроводности можно найти очень важный параметр полупроводника – ширину запрещенной зоны полупроводника DЕ_g и энергию ионизации примесных атомов DЕ_d. Ширину

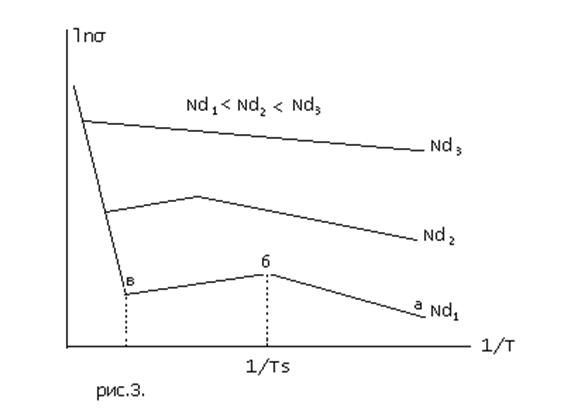
Рис.3. Температурная зависимость электропроводности полупроводника.

запрещенной зоны можно определить из наклона кривой на участке вг по формуле:

(14)

а энергию ионизации донорных примесей из участка аб

(15)

Температура начала собственной проводимости зависит от концентрации атомов примеси и их природы. С ростом концентрации атомов примеси температура начала собственной проводимости смещается в высокотемпературную область и наклон участка аб к оси температуры уменьшается. При достаточно высокой концентрации примеси примесная проводимость не зависит от температуры (рис.3), т.к. при комнатной температуре вся примесь ионизирована. Такие полупроводники называют полуметаллами.

Все полученные выводы справедливы и для акцепторного полупроводника.

Измерительная установка и методика эксперимента

Образец германия – прямоугольный параллелепипед размерами 2х3х10мм, площадью поперечного сечения S = 6 мм² помещен в печь. На образец припаяны оловом два зонда на расстоянии l см друг от друга, которые служат для измерения сопротивления на этом участке.

Электропроводность подсчитывается по формуле:

(16)

Нагревательная печка питается от ЛАТРа. Температура измеряется с помощью термопары хромель – алюмель. С помощью градуировочной таблицы значения термоэдс переводятся в градусы. Измерения температуры производят с помощью потенциометра ПП –63 и градуировочной таблицы термопары хромель – алюмель. Для измерения сопротивления используется цифровой прибор В7 – 35.

Порядок выполнения работы

1. Измерить температурную зависимость электропроводности:

- собрать схему согласно рис.4;

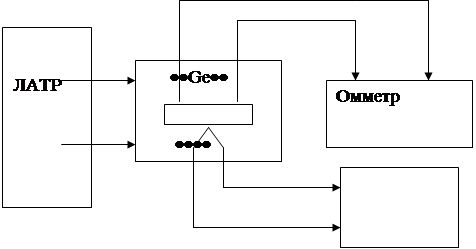
Рис.4. Блок - схема установки.

- включить ток через образец, измерить сопротивление образца при комнатной температуре;

- включить нагреватель, постепенно нагревая образец измерить сопротивление соответствующее каждой температуре. Измерения производить при термоэдс от 0,5 до 5,0 mV через каждые 0,5 mV.

- Результаты занести в таблицу1:

Таблица 1.

№

Т, ^0С

1000/Т

s

lns

2. Построить график температурной зависимости электропроводности в координатах lns = f(1000/T), найти тангенс угла наклона прямой tga и определить ширину запрещенной зоны по формуле

DE_g = 2ktga

Рассчитать удельное сопротивление r при комнатной температуре и температурный коэффициент удельного сопротивления a_r образца германия.

3. По параметрам, предложенным преподавателем рассчитать величину N_c, N_v, концентрации носителей заряда при различных температурах (40, 90, 125 ⁰С), температуру начала собственной проводимости и истощения примеси.

Контрольные вопросы

1. Что такое ширина запрещенной зоны полупроводника?

2. Объясните механизм электропроводности в собственном и примесном полупроводнике.

3. Что такое собственный полупроводник? Может ли примесный полупроводник обладать собственной проводимостью?

4. Каким образом по температурной зависимости концентрации носителей заряда и проводимости полупроводника можно определить ширину запрещенной зоны?

5. При комнатной температуре средняя энергия тепловых колебаний атомов существенно меньше ширины запрещенной зоны полупроводников. Каким образом электроны из валентной зоны могут переходить в зону проводимости в собственном полупроводнике?

6. Сколько электронов находится на уровне Ферми в собственном полупроводнике? Как влияет температура на положение этого уровня?

Литература

1. Пасынков В.В., Сорокин В.С. Материалы электронной техники, СПб.: Изд- во «Лань», 2002, 368 С.

2. Шалимова К.В. Физика полупроводников: Учебник. – СПб.:Издательство «Лань», 2010. - 392С.

3. Смит Р. Полупроводники: Учебное пособие. – М: Мир, 1982. – 560 С.

Лабораторная работа № 2

Исследование электропроводности металлов

Цель работы: Исследовать температурную зависимость электропроводности металлов. Рассчитать температурный коэффициент сопротивления.

Требуемое оборудование: 1. Блок амперметра-вольтметра АВ1 1 шт.

2. Блок генератора напряжений ГН1 1 шт.

3. Стенд с объектами исследования С3-ТТ01 1 шт.

4. Соединительные провода с наконечниками Ш4-Ш1. 6 шт.

Теория

Порядок выполнения работы

Контрольные вопросы

Литература

Теория

Металлы обычно определяются как вещества пластичные, с характерным блеском, хорошо проводящие электрический ток и теплоту.

Для электропроводности металлов типичны:

· низкое значение удельного сопротивления при комнатной температуре (от сотых долей до единиц мкОм/м);

· значительный рост сопротивления при повышении температуры, близкий к прямой пропорциональной сопротивление уменьшается до очень малого значения, составляющего для наиболее чистых металлов 10^-5 или даже меньшую долю сопротивления при комнатой температуре.

Электропроводность σ металлов зависит от концентрации свободных электронов n и их подвижности μ

, (1)

где e - заряд электрона;

m - масса носителей заряда;

- среднее время свободного пробега носителей заряда.

Концентрация свободных электронов в металле составляет примерно n ≈ 10²⁸ м^-3, т.е. того же порядка, что и число атомов в 1 м³. В проводимости принимают участие валентные электроны. Они обобществляются кристаллической решеткой металла при очень низких абсолютных температурах. Другие электроны очень прочно связаны с атомами и не становятся свободными даже при очень высоких температурах. Из этого следует, что концентрация носителей заряда в металлах не зависит от температуры. Среднее время свободного пробега носителей заряда при повышении температуры металлов уменьшается по закону , что объясняется рассеянием их на фононах. Сделанное утверждение не относится к области очень низких температур, при которых основным становится рассеяние на примесях и других дефектах кристаллической решетки. Поскольку электропроводность обратно пропорциональна удельному электрическому сопротивлению вещества , то сопротивление металла R₁ линейно растет с повышением его абсолютной температуры Т₁ по закону

R₁ = R₀ (1+α_R ΔT) , (2)

где R₀ - сопротивление при некоторой условной температуре T₀ (обычно при 273К); ΔТ = (Т₁ - Т₀), α_R - температурный коэффициент сопротивления, показывающий относительное изменение величины сопротивления при изменении температуры на один градус.

Если известны размеры проводника, то возможно определить удельное сопротивление проводника по формуле:

, (3)

где R - сопротивление проводника, S и l – площадь поперечного сечения и длина проводника, соответственно.

Удельное сопротивление металлических проводников

, (4)

где – средняя длина свободного пробега.

В чистых металлах совершенной структуры единственной причиной, ограничивающей длину свободного пробега электронов, являются тепловые колебания атомов в узлах кристаллической решетки. С ростом температуры увеличиваются амплитуды тепловых колебаний атомов, а это, в свою очередь, усиливает рассеяние электронов и вызывает возрастание удельного сопротивления.

С понижением температуры могут уменьшаться не только амплитуды тепловых колебаний атомов, но и частоты колебаний. Поэтому в области низких температур рассеяние электронов тепловыми колебаниями узлов кристаллической решетки становится не эффективным. Взаимодействие электрона с колеблющимися атомами лишь незначительно изменяет импульс электрона. В теории колебаний атомов решетки температуру оценивают относительно некоторой характеристической температуры, которую называют температурой Дебая (Ѳ_Д). Температура Дебая определят максимальную частоту тепловых колебаний , которые могут возбуждаться в кристалле:

, (5)

где h –постоянная Планка, а k – постоянная Больцмана.

Эта температура зависит от сил связи между узлами кристаллической решетки и является важным параметром твердого тела. При Т > Ѳ_Д удельное сопротивление металлов изменяется линейно с температурой

, (6)

где В = const. Как показывает эксперимент, линейная аппроксимация температурной зависимости ρ(Т) справедлива и до температур (2/3)Ѳ_Д, где ошибка не превышает 10%. Для большинства металлов Ѳ_Д не превышает 400 – 450К. Поэтому линейное приближение обычно справедливо при температурах от комнатной и выше. В низкотемпературной области Т << Ѳ_Д спад ρ обусловлен постепенным исключением все новых и новых частот тепловых колебаний (фононов), теория показывает степенную зависимость ρ ~ Т⁵.

Типичная кривая изменения удельного сопротивления металлического проводника в зависимости от температуры представлена на рис. 1.

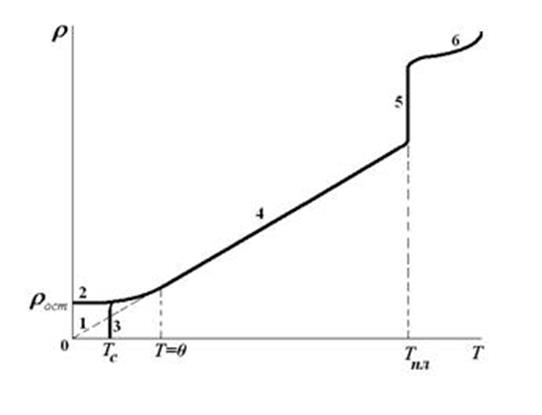
Рис.1. Температурная зависимость удельного сопротивления металлических проводников.

Как следует из формулы (6), удельное сопротивление проводников зависит от температуры линейно (ветвь 4 на рис.1), за исключением низких температур Т < Ѳ_Д , и температур больших температуры плавления Т > Т_ПЛ.

У чистых металлов совершенной структуры при стремлении температуры к 0 К удельное сопротивление стремится к нулю (пунктирная линия, ветвь 1), а длина свободного пробега устремляется в бесконечность. Далее в пределах переходной области наблюдается быстрый рост удельного сопротивления по степному закону вплоть до Т = Ѳ_Д.

У технически чистых проводников (с очень малым количеством примесей) на небольшом участке, составляющем несколько кельвинов, значение ρ перестает зависеть от температуры и становится постоянным (ветвь 2). Его называют остаточным удельным сопротивлением ρ_ОСТ. Величина ρ_ОСТ определяется только примесями. Чем чище металл, тем меньше ρ_ОСТ

Вблизи абсолютного нуля возможно и другая зависимость ρ от температуры. В узкой области температур, составляющей несколько кельвинов, у ряда металлов может наступить состояние сверхпроводимости, а именно, при некоторой температуре Т_С удельное сопротивление ρ скачком падает практически до нуля (ветвь 3). Это состояние называют сверхпроводимостью, а проводники, обладающие этим свойством, называют сверхпроводниками.

Линейный участок (ветвь 4 на рис.1) в температурной зависимости ρ(Т) у большинства металлов простирается до температур, близких к точке плавления Т_ПЛ. Исключение из этого правила составляют ферромагнитные металлы, в которых имеет место дополнительное рассеяние электронов на нарушениях спинового порядка. Вблизи точки плавления, т. е. в области , начало которой отмечено на рис.1 температурой Т_ПЛ и в обычных металлах может наблюдаться некоторое отступление от линейной зависимости.

При переходе из твердого состояния в жидкое у большинства металлов наблюдается увеличение удельного сопротивления приблизительно в 1,5 - 2 раза (ветвь 5 и 6), хотя имеются и необычные случаи: у веществ со сложной кристаллической структурой, подобных висмуту и галлию, плавление может сопровождаться уменьшением ρ.

Относительное изменение удельного сопротивления при изменении температуры на один кельвин (градус) называют температурным коэффициентом удельного сопротивления α_r :

. (7)

где Δr = (r₁ - r₀) т.е .разность удельного сопротивления проводника при температуре Т₁ и Т₀, соответственно. Размерность температурного коэффициента ТК обратно пропорциональна размерности температуры и все ТК выражаются в К^-1 ', т.е

[α] = К^-1.

Удельное сопротивление металлов при повышении температуры возрастает. Следовательно, температурный коэффициент удельного сопротивления величина положительная.

Положительный знак α_r соответствует случаю, когда удельное сопротивление в окрестности данной точки возрастает при повышении температуры. Для всех металлов температурный коэффициент больше нуля. При изменениях температуры он будет незначительно меняться. Поэтому, если изменение температуры невелико, то температурный коэффициент можно считать постоянным, и равным среднему значению из этого интервала температур.

Растворы электролитов с ростом температуры сопротивление уменьшается. То есть для них температурный коэффициент будет меньше нуля. Сопротивление проводника зависит от удельного сопротивления проводника и от размеров проводника. Так как размеры проводника при нагревании меняются незначительно, то основной составляющей изменения сопротивления проводника является удельное сопротивление.

Коэффициент α для металлов положителен, почти не меняется с температурой и мал по абсолютной величине по сравнению с α для полупроводников. В таблице 1 приведены значения температурных коэффициентов сопротивления для некоторых металлов.

Таблица 1

Металл	Медь	Вольфрам	Платина	Хром	Никель	Палладий	Серебро
α, К^- 1.10^-3	4,3	5,0	3,9	2,4	6,7	3,6	4,1

Заметим, что зависимость (2) нельзя экстраполировать до абсолютного нуля температур, при стремлении к которому сопротивление обычных металлов (не сверхпроводников) стремится к некоторой конечной величине, обусловленной наличием примесей и дефектов решетки.

Величина α_r также является функцией температуры. В области линейной зависимости ρ(Т) справедливо выражение:

, (8)

где ρ₀ и α_ρ — удельное сопротивление и температурный коэффициент удельного сопротивления, отнесенные к началу температурного диапазона, т.е. температуре Т₀; ρ — удельное сопротивление при температуре Т. Из вышеприведённых формул следует, что значение α_ρ чистых металлов должно быть близким к 1/Т. Согласно экспериментальным данным большинство металлов имеют при комнатной температуре α_ρ ≈ 0,004 К^-1 . Несколько большим α_ρ характеризуются ферромагнитные металлы.

На практике при измерении α_ρ часто бывает полезной следующая формула:

(9)

где α_R — температурный коэффициент сопротивления данного резистора; α_l — температурный коэффициент линейного расширения материала.

У чистых металлов α_R >> α_l , поэтому у них α_ρ ≈ α_R. Однако для термостабильных металлических сплавов такое приближение оказывается несправедливым.

Методика проведения эксперимента

В качестве металлического образца в стенде С3-ТТ01 установлен металлический терморезистор (платиновый тонкопленочный резистор). Для нахождения сопротивления терморезистора можно воспользоваться методом амперметра - вольтметра по закону Ома.

(10)

Для проведения измерений электрическая схема представлена на рис. 1. Т. к. измеряемое сопротивление R намного меньше внутреннего сопротивления вольтметра, то вольтметр подключен параллельно измеряемому сопротивлению.

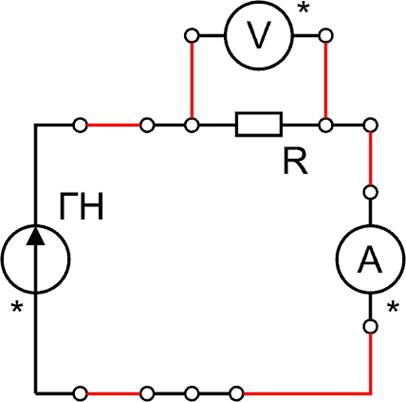
Рис. 2. Электрическая схема измерений электропроводности металлов.

Порядок выполнения работы

1. Снять ВАХ (U = f(I)) металлического образца при двух различных температурах образца. Рекомендуемые значения температуры Т = 300К и Т= 360К. Рекомендуемый диапазон изменения тока 0 – 5 мА. Построить графики.

2. Снять зависимость сопротивления металлического образца от температуры R = f(T) при постоянном токе I = const. Рекомендуемое значение 1 мА. Т.к схема питается от генератора напряжения, то при нагреве образца ток может изменяться. Поэтому необходимо перед измерением установить требуемое значение тока.

3. Рассчитайте по формулам (7) и (9) значение температурного коэффициента сопротивления α_r. По таблице 1 определите материал, из которого сделан терморезистор.

Примечание: Для быстрого охлаждения образца воспользуйтесь вентилятором.

Контрольные вопросы

1. Какие признаки типичны для электропроводности металлов?

2. Как связаны электропроводность и удельное сопротивление проводников?

3. Охарактеризуйте температурные изменения удельного сопротивления металлических проводников.

4. Какой параметр характеризует температурные изменения удельного сопротивление? Запишите формулу.

5. Каков физический смысл температурного коэффициента удельного сопротивления? В каких единицах он измеряется?

6. Что такое температура Дебая? Запишите формулу.

7. О чем говорит положительный знак α_r металлических проводников?

Список литературы

1. Физика твердого тела: Методическое руководство к лабораторным работам №40-45 по физике. – Новосибирск: Новосибирский государственный технический университет, 2003. – 74 С.

2. Пасынков В.В., Сорокин В.С. Материалы электронной техники. – СПб.: Изд – во Лань, 2004. – 378 С.

Лабораторная работа №3

Определение концентрации и холловской подвижности основных носителей заряда

Цель работы: определение концентрации, знака и холловской подвижности основных носителей заряда в полупроводниках на основании измерений эффекта Холла. Измерения проводятся в постоянном магнитном поле на образцах германия.

Теория

Порядок выполнения работы

Контрольные вопросы

Литература

Теория

При одновременном действии магнитного и электрического поля на свободные носители заряда в твердом теле возникают вторичные явления, называемые гальваномагнитными. Эффект Холла является одним из наиболее важных среди этих явлений, с помощью которого можно определять ряд параметров полупроводника.

Движение заряда в магнитном поле

На носители с электрическим зарядом е, движущимся со скоростью в магнитном поле , действует сила Лоренца

(1)

Направление этой силы зависит от знака носителей заряда е и векторного произведения скорости на вектор напряженности магнитного поля . Если ^, то под действием силы Лоренца произойдет отклонение носителей тока в направлении, перпендикулярном и , т.е. направление векторов будет таким, как показано на рис.1. Произойдет пространственное разделение носителей заряда, а это приведет к появлению электрического поля. В стационарном состоянии электрическая сила , действующая на заряд, будет равна силе Лоренца

= = (2)

где - магнитная индукция, m - относительная проницаемость материала образца, m₀ - магнитная постоянная.

Если концентрация движущихся носителей заряда равна n и все они имеют отрицательный заряд, то образовавшееся электрическое поле можно представить через плотность тока , ( S- площадь образца) в виде

(3)

Рис.1.

В этом выражении - постоянная Холла или коэффициент Холла.

Явление образования электрического поля и соответствующей ему разности потенциалов при помещении образца, по которому протекает электрический ток, в магнитное поле называют эффектом Холла. Явление было открыто в 1879 г. на образце из металла. При рассмотрении вопроса считалось, что . В реальных условиях скорость носителей заряда не постоянна. При более строгом рассмотрении вопроса необходимо учесть статистическое распределение носителей заряда по скоростям. Более строгое описание эффекта Холла основывается на решении кинетического уравнения Больцмана.

Эффект Холла в полупроводниках.

Эффект Холла является одним из гальваномагнитных эффектов. Действие магнитного и электрического полей на носители электрического заряда зависит от величины напряженности полей. При измерении эффекта Холла применяются слабые электрические и магнитные поля, т.е. действие электрического поля с напряженностью Е не должно приводить к изменению температуры образца за счет выделяемого в образце диполевого тепла.

Сущность эффекта Холла заключается в следующем. Если пластину полупроводника, по которой проходит электрический ток, поместить в магнитное поле, перпендикулярное току и магнитному полю, возникнет разность потенциалов. Последняя получила название э.д.с. Холла.

Появление э.д.с. Холла обусловлена тем, что на носители заряда движущиеся со скоростью , в магнитном поле с индукцией действует сила Лоренца (1),отклоняющая их к одной из боковых граней пластины. Направление действие силы Лоренца можно определить по известному правилу левой руки, относя его к техническому направлению тока.

С учетом того, что и

(4)

Отсюда следует, что направление силы Лоренца не зависит от знака носителей заряда, а определяется лишь направлениями электрического и магнитного полей. При заданных направлениях и электроны и дырки в полупроводниках отклоняются в одну и ту же сторону. Поэтому полярность э.д.с. Холла в полупроводнике n – типа оказывается противоположной полярности, получаемой в материале p – типа, что и используется для определения типа электропроводности полупроводников.

По результатам измерения э.д.с. Холла можно определить не только знак носителей заряда, но и рассчитать их концентрацию, а при известном значении удельной проводимости полупроводника найти и подвижность носителей заряда.

Полупроводники с носителями заряда одного типа

Смещение носителей заряда в поперечном направлении в полупроводнике прекратиться, когда сила Лоренца уравновеситься силой поперечного электрического поля сместившихся зарядов. Если поверхность пластины полупроводника перпендикулярна линиям магнитной индукции, то отражением такого динамического равновесия является равенство

evB = eE_H (5)

где E_H– напряженность холловского поля.

Считая электрическое поле однородным, получим

E_Hx =U_H (6)

Площадь поперечного сечения пластины

S = xd (7)

где x – ширина; d - толщина пластины.

Используя выражения (5) – (7) и J = env, для полупроводника p – типа получим

(8)

Поперечную э.д.с. U_H, ток I, магнитную индукцию B и толщину полупроводниковой пластины можно легко измерить, что позволит найти численное значение коэффициента Холла R_H.

z

I

U_x

x

y

Рис.2. Эффекта Холла.

Для полупроводника n – типа результат совершенно аналогичен с той лишь разницей, что концентрация дырок заменяется концентрацией электронов. Кроме того, направление напряженности поперечного поля E_H будет противоположным. Условно принято относить знак э.д.с. Холла к коэффициенту Холла. Поэтому коэффициент Холла у полупроводника n – типа отрицателен.

Коэффициент Холла определяется следующим образом

R_H = A/(ep), для p – типа

R_H = - A/(en), для n – типа. (9)

Множитель А изменяется для полупроводников различных групп (с атомной или ионной решеткой) изменяется в зависимости от механизма рассеяния при различных температурах всего от 1 до 2.

Как видно из (8) значение R_Hзависит от концентрации носителей заряда, а следовательно, и от температуры. Измеряя э.д.с. Холла в некотором диапазоне температур, получают экспериментальные данные для построения зависимости концентрации носителей заряда от температуры, по которой можно вычислить энергию ионизации доноров или акцепторов, концентрацию электрически активной примеси. Если при этом одновременно измерять удельное сопротивление материала, то с помощью формулы

m_n = g/(en) = R_H/r (10)

можно найти подвижность носителей заряда и построить ее температурную зависимость.

Рассчитанная таким образом подвижность называют «холловской». Численное значение ее может расходится с подвижностью, определенной у того же материала другими методами, например, по времени перемещения возбужденного облака носителей заряда на определенное расстояние в образце с известным ускоряющим полем. Последнюю называют дрейфовой подвижностью. Холловская подвижность может быть больше дрейфовой вследствие временных задержек перемещающихся носителей заряда на ловушках захвата.

Полупроводники с носителями заряда двух типов.

Если концентрация неосновных носителей такова, что они начинают заметно влиять на движение частиц в полупроводнике, находящемся в магнитном поле, то необходимо учитывать оба типа носителей. Коэффициент Холла с учетом носителей двух типов

(11)

Положив либо n = 0, либо p = 0 можно получить выражение (9).

Зная для одного и того же образца коэффициент Холла и электропроводность , можно рассчитать холловскую подвижность носителей тока:

. (12)

U₂

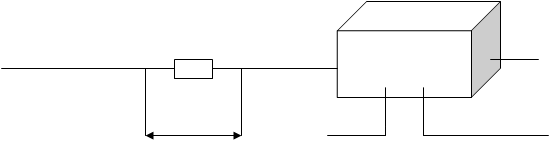
R_эт I

U_H

U₁

Рис. 3. Методика эксперимента по измерению эффекта Холла.

U₁ – падение напряжения на эталонном сопротивлении, U₂ – разность потенциалов между контактами для измерения проводимости образца, U₃ – холловский потенциал, равный U_H.

Порядок выполнения работы

В работе используется стенд по физике полупроводников СФП-5, предназначенный для измерения электрофизических параметров полупроводниковых материалов и универсальная измерительная головка (УИГ), содержащая образец германия n-типа, расстояние между зондами 15 мм, размеры образца 20х3х2,5 мм. УИГ состоит из германиевого образца, на котором располагаются два миниатюрных электронагревателя. Первый служит для относительно равномерного нагрева, а второй – для создания разности температур (см. рис.)

1 2

Т₁ Т₂

3

Термопары Т₁ и Т₂ служат для определения усредненной температуры при равномерном нагреве, а также для измерения разности температур

Кроме того, один проводник термопары используется как токопроводящий при наблюдении эффекта Холла и снятии зависимости электропроводности от температуры.

В первом случае эдс Холла снимается с 1-го и 3-го вольфрамового зондов, во втором – с 1-го и 2-го.

В работе также используется цифровой вольтметр В7-16 (В7- 40), либо другой с R_вхÞ 10 мОм и пределами измерения U от 0,05 мВ до 10 В.

1. УИГ помещают между полюсными наконечниками электромагнита. К клеммам « - » и «U» панели блока управления подключается вольтметр В7-16. Через образец пропускают ток, для этого переключатель П3 устанавливают в положение «U_хол.», П2 – «Выкл.», ручками «Ток образца» устанавливают необходимое значение тока.

2. Измеряют паразитную ЭДС между холловскими зондами образца при различной полярности тока.

3. Включают электромагнит, напряженность магнитного поля которого регулируется потенциометром «Ток магнита» и измеряют значение ЭДС Холла. Для исключения влияния паразитной разности потенциалов, возникающей за счет несимметричного расположения поперечных зондов необходимо проводить измерения (V_X) при двух полярностях магнитного поля, меняя направление тока через обмотку электромагнита.

4. Исходя из полученных значений U_Н, и размеров образца легко рассчитать концентрацию носителей заряда

(13)

коэффициент Холла по формуле

(14)

подвижность носителей заряда

. (15)

Здесь r - удельное сопротивление образца германия (r = 0,195 Ом м). Так как германий относится к слабо магнитным материалам, то при расчетах принять m = 1.

Для исключения влияния паразитной разности потенциалов, возникающей за счет несимметричного расположения поперечных зондов необходимо проводить измерения (V_X) при двух полярностях магнитного поля, меняя направление тока через обмотку электромагнита. Результаты измерений занести в таблицу

Таблица 1

№

Iмагн, А

В, Тл

iобр, млА

UН^+В

UН^-В

UНср

5. Результаты представить в виде графика U_Н = f(B). Подсчитать по известной методике значения U_Ни построить график U_Н = f(B) при I_обр = const.

Контрольные вопросы

1. Что такое эффект Холла?

2. Объясните характер движения носителей заряда при наличии электрического и магнитного полей.

3. Чему равна величина силы Лоренца, от чего она зависит? Как определить направление этой силы?

4. Какие параметры полупроводника можно определить с помощью эффекта Холла?

5. Почему холловская подвижность отличается от дрейфовой?

6. Какие физические свойства полупроводников влияют на значение э.д.с. Холла?

Литература

1. Смит Р. Полупроводники, М.: «Мир», 1982 г., 560 С.

2. Шалимова К.В. Физика полупроводников: Учебник. – СПб.:Издательство «Лань», 2010. - 392 С.

3. Пасынков В.В., Сорокин В.С. Материалы электронной техники, СПб.: Изд- во «Лань», 2002, 368 С.

Лабораторная работа №4

Исследование электропроводности тугоплавких металлов и сплавов высокого сопротивления.

Цель работы: Определить сопротивление и его зависимость от температуры для некоторых металлов и сплавов. Выполнить расчет температурного коэффициента сопротивления.

Требуемое оборудование: 1. Измеритель электропроводности ИЭП1 – 1 шт.

2. Измерительные кассеты – 3 шт.

Теория

Порядок выполнения работы

Контрольные вопросы

Литература

Теория

Важнейшими практически применяемыми в электротехнике проводниковыми материалами являются металлы и сплавы. Основными электрическими характеристиками проводниковых материалов являются следующими:

1. Удельная проводимость или обратная ей величина – удельное сопротивление.

2. Температурный коэффициент удельного сопротивления ТКR (α_R).

Электросопротивление металлов является структурно - чувствительным параметром. Для чистых металлов с наиболее правильной кристаллической решеткой значения удельного сопротивления являются минимальными. И наоборот, наличие примесей и дефектов в решетке приводит к увеличению r. Экспериментальные исследования показывают, что весьма небольшие изменения в структуре металлов, обусловленные, например, наличием точечных дефектов или дислокаций, приводят к заметным изменениям величины электросопротивления. Электросопротивление весьма чувствительно также к наличию в металлах атомов примесей. Заметно меняется оно и при изменении фазового состава материалов, в частности, в условиях термического и деформационного старения. В связи с этим, прецизионное изменение электросопротивления весьма эффективным макроскопическим методом изучения структурного состояния металлов.

Удельное электрическое сопротивление r связано с сопротивлением проводника R любой длины l и площади поперечного сечения S формулой

, . (1)

Диапазон значений удельного сопротивления металлических проводников (при комнатной температуре) довольно узок: от 0,016 мкОм·м для серебра и примерно до 10 мкОм·м для железохромалюминиевых сплавов, т. е. он занимает всего три порядка. Значения удельного сопротивления некоторых металлов приведены в табл. 1.

Величина удельного сопротивления металлического проводника может быть выражена на основании представлений электронной теории металлов:

, (2)

где m – масса электрона;

v_T – средняя скорость теплового движения электрона внутри металлического проводника;

е – заряд электрона;

n₀ – число электронов в единице объема проводника;

λ – средняя длина свободного пробега электронов.

Для различных металлов скорости хаотического теплового движения электронов v_T примерно одинаковы. Концентрации свободных электронов n₀ в различных металлах также различаются незначительно (в пределах 10%). Поэтому значение удельного сопротивления и его зависимость от различных факторов определяются в основном средней длиной свободного пробега электронов в проводнике, которая обусловлена структурой материала. Все чистые металлы с наиболее правильной кристаллической решеткой характеризуются наименьшими значениями удельного сопротивления (см. табл. 1).

Таблица 1

Металлы и сплавы	Удельное сопротивление r , мкОм·м	Температурный коэффициент сопротивления αR , К^–1
Серебро	0,015	4,1·10^–3
Золото	0,023	3,9·10^–3
Алюминий	0,026	4,1·10^–3
Медь	0,017	4,3·10^–3
Железо	0,097	6,2·10^–3
Вольфрам	0,055	5,0·10^–3
Нихром	1 – 1.2	(1 – 2)·10^–4
Константан	0,45 – 0,52	(5 – 25)·10^–6
Манганин	0,42 – 0,48	(5 – 30)·10^–6

Зависимость электрического сопротивления металлов от температуры

Электрическое сопротивление металлов изменяется пропорционально температуре, а при низких температурах – пропорционально температуре в пятой степени. Во многих металлах при криогенных (гелиевых) температурах электрическое сопротивление практически становится равным нулю (явление сверхпроводимости здесь не рассматривается).

В интервале температур от 0 до 100⁰ С можно считать, что сопротивление проводника в первом приближении изменяется по закону

(3)

Изменение удельного сопротивления металлического проводника с температурой принято характеризовать температурным коэффициентом удельного сопротивления ТКr или a_r (К^-1).

В диапазоне средних и высоких температур температурный коэффициент электрического сопротивления

(4)

где r₁ и r₂ - удельное электрическое сопротивление материала при температурах Т₁ и Т₂, соответственно. Температуру Т₁ обычно принимают равной 20⁰ С, и поэтому значение a_r часто приводится при этой температуре. Из формулы (4) следует, что значение a_r чистых металлов должно быть близким к 1/Т. Для большинства металлов вблизи 290 К величина a_r » 4 10^-3 K^-1 . Несколько большим a_r характеризуются ферромагнитные металлы.

В области линейной зависимости r(Т), используя значение коэффициента a_r, определенное для интервала температур DТ, можно достаточно точно определить удельное сопротивление r₂ для любой температуры T₂ внутри этого интервала:

(5)

Правило Маттиссена

Примеси и нарушения кристаллической решетки приводят к увеличению удельного сопротивления. Это связано с рассеянием электронов на дефектах структуры, что приводит к снижению длины свободного пробега λ и соответственно к увеличению r.

Удельное сопротивление металлов связано в основном с рассеянием энергии свободных электронов на дефектах кристаллической решетки, к которым относятся примесные атомы, вакансии, дислокации, и тепловых колебаний собственных атомов. Рассеяние на статических дефектах не зависит от температуры. Поэтому при приближении температуры к абсолютному нулю сопротивление реальных металлов стремиться к некоторому постоянному значению, называемому остаточным сопротивлением. Поэтому удельное сопротивление

, (6)

где r_тепл. – удельное сопротивление, обусловленное в основном тепловыми колебаниями решетки; r_ост. – удельное сопротивление, вызванное наличием дефектов в кристаллической решетке, которое не зависит от температуры.

Соотношение (6) называется правилом Маттиссена. Исключение из этого правила составляют сверхпроводящие металлы, в которых сопротивление исчезает ниже некоторой критической температуры.

Наиболее существенный вклад в остаточное сопротивление вносит рассеяние на примесях, причем любая примесная добавка приводит к повышению r, даже если она обладает повышенной проводимостью по сравнению с основным металлом.

Правило Маттиссена учитывает рост электрического сопротивления при повышении температуры за счет увеличения амплитуды тепловых колебаний атомов и справедливо не только для чистых металлов, но и для слаболегированных сплавов. Увеличение содержания примеси ведет к росту остаточного электрического сопротивления. Температурная зависимость электрического сопротивления, характерная для основного металла, при этом сохраняется: , где r_спл и r_м - удельное электрическое сопротивление сплава и металла основы, соответственно. Отсюда следует, что температурный коэффициент электрического сопротивления сплава a_спл. меньше температурного коэффициента чистого металла:

(7)

Для ферромагнетиков и антиферромагнетиков

, (8)

где r_м - магнитное сопротивление, связанное с рассеянием электронов на магнитных неоднородностях (магнонах). В общее электрическое сопротивление магнетика и антиферромагнетика, определяющееся выражением (7), магнитное сопротивление вносит существенный вклад. Таким образом, электрическое сопротивление зависит как от магнитной структуры, так от дефектного состояния кристаллической решетки металлов и сплавов.

Коэффициент α_R называют температурным коэффициентом сопротивления. Он показывает относительное изменение сопротивления при изменении температуры. Согласно ГОСТР 8.625 - 2006 температурный коэффициент сопротивления металлического терморезистора (медь, никель, платина) α_R определяется по формуле

(9)

где R₁₀₀, R₀ – значения сопротивления соответственно при 100⁰ С и 0⁰ С.

Коэффициент для металлов положителен, почти не меняется с температурой. Заметим, что зависимость нельзя экстраполировать до абсолютного нуля температур, при стремлении к которому сопротивление обычных металлов (не сверхпроводников) стремится к некоторой конечной величине, обусловленной наличием примесей и дефектов решетки.

Температурные коэффициенты для чистых металлов всегда больше, чем для сплавов из этих металлов. Температурные коэффициенты сплавов могут быть близки к нулю, а в некоторых случаях могут принимать даже отрицательные значения.

Электрическое сопротивление сплавов

Удельное сопротивление сплавов определяется в основном наличием примесей и нарушением структуры входящих в них металлов. Особенно резко оно возрастает, когда при сплавлении двух металлов образуется твердый раствор, т.е. они совместно кристаллизуются. При этом атомы одного металла входят в кристаллическую решетку другого.

Статическое распределение атомов разных сортов по узлам кристаллической решетки вызывает значительные флуктуации периодического потенциального поля кристалла, что, в свою очередь, приводит к сильному рассеянию электронов. Как и в случае металлов, полное сопротивление сплава можно описать правилом Маттиссена.

Специфика твердых растворов состоит в том, что r_ост. может существенно (во много раз) превышать тепловую составляющую.

Для многих двухкомпонентных сплавов изменение r_ост. в зависимости от состава хорошо описывается параболической зависимостью вида

(10)

где С – константа, зависящая от природы сплава; х_А и х_В – атомные доли компонентов в сплаве.

Соотношение (9) получило название закона Нордгейма. Из него следует, что в бинарных твердых растворах А – В остаточное сопротивление увеличивается как при добавлении атомов В к металлу А, так и при добавлении атомов А к металлу В, причем это изменение характеризуется симметричной кривой. В непрерывном ряду твердых растворов удельное сопротивление тем больше, чем дальше по своему составу сплав отстоит от чистых компонентов.

В данной работе кроме чистой меди исследуется вольфрам, сплавы константан и нихром.

Константан – сплав высокого сопротивления, слабо зависящий от температуры. Состоит из 60 % меди и 40 % никеля. Константан имеет удельное сопротивление 0,5 Ом м, плотность 8,9 кг/дм³, прочность на разрыв 40 – 50 кг/мм². Константан применяется для изготовления реостатов и электронагревательных сопротивлений, если их рабочая температура не превышает 400 – 450⁰ С.

Нихром – сплав высокого сопротивления никеля и хрома. К нихромам относится также ферронихром, который, кроме никеля и хрома, содержит железо (58 – 62 % никеля, 15 – 17 % хрома, остальное – железо). Плотность нихрома 8,4 кг/дм³, прочность на разрыв 70 кг/мм², удельное сопротивление около 1,0 Ом м. Нихром выпускается в виде проволоки и ленты, которые идут на изготовление спиралей электронагревательных приборов и печей, имеющих рабочую температуру до 1000⁰ С.

Методика проведения эксперимента

Исследование зависимости сопротивления проводниковых материалов от температуры проводятся с помощью прибора ИЭП1 (рис. 1). Он содержит термокамеру, терморегулятор и измеритель сопротивлений в диапазоне 10...10¹³ Ом.

Применяемый в приборе метод измерения сопротивлений основан на сравнении измеряемого сопротивления и образцового сопротивления с помощью операционного усилителя, охваченного глубокой обратной связью (рис. 2). В приборе имеются два диапазона измерений и используются две шкалы – линейная и обратно пропорциональная. Измерения сопротивлений в диапазоне 10²...10⁶ Ом проводятся по линейной шкале, а в диапазоне 10⁷...10¹³ Ом – по обратно пропорциональной шкале.

Рис.1. Прибор «Измеритель электропроводности ИЭП1».

Для включения прибора необходимо нажать кнопку “Сеть” (рис. 2), при этом загорится индикатор результата измерения, индикатор выбора температуры, индикатор выбора канала.

Исследуемые образцы находятся в измерительной кассете ИК1. Для ее установки в прибор необходимо поднять шторку, установить кассету с образцами в термокамеру прибора до упора. При этом шторка должна опуститься.

Кнопками «+» и «-» на левой части прибора устанавливается требуемый диапазон измерений. Соответствующей кнопкой на передней панели устанавливается требуемый канал для измерения. Контроль выбора канала осуществляется с помощью загорающегося индикатора.

С помощью кнопок «+» и «-» на правой части прибора устанавливается требуемое значение температуры термокамеры. При первом нажатии кнопки на индикаторе «Температура» высветится установленное значение температуры. При повторном нажатии кнопки произойдет коррекция устанавливаемой температуры. Через 2 секунды после завершения установки индикатор перейдет в режим отображения текущей температуры. Для отключения терморегулятора необходимо установить температуру менее 30⁰С. При этом на экране высветится сообщение “OFF”.

Примечание. При работе прибора на индикаторе «Сопротивление» могут отображаться следующие сообщения: «L» – измеряемое сопротивление ниже выбранного диапазона; «H» – измеряемое сопротивление выше выбранного диапазона.

Для исследуемых в работе образцов, имеющих сопротивление ниже 10⁶ Ом, измерения проводятся по линейной шкале.

Сначала измеряют сопротивление металла при комнатной температуре R_к, затем нагревают металл и проводят измерения его сопротивления при соответствующих температурах. Строят график зависимости сопротивления металла от его температуры R = f(T) (рис.2).

Согласно формуле (3), этот график имеет вид прямой линии, продолжение которой (экстраполяция) пересекает ось ординат в точке R₀.

Образцы. Первый канал: медь – поперечное сечение S = 0,1 мм², длина l = 50 м, константан – поперечное сечение S = 0,3 мм², длина l = 4 м. Второй канал: Вольфрам - поперечное сечение S = 0,1 мм², длина l = 4 м; нихром - поперечное сечение S = 0,2 мм², длина l = 2 м.

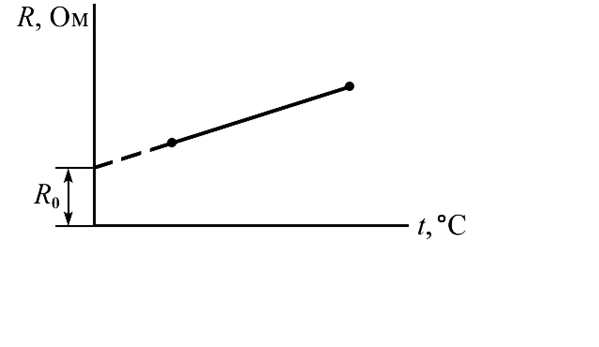
Рис. 2. Температурная зависимость сопротивления R от температуры Т.

Порядок выполнения работы

1. Включите кнопку «Сеть» и установите требуемый канал для измерения. Сопротивление первого материала (медь) отображается по каналу1. Сопротивление второго материала (константан) - по каналу 2.

2. Установите требуемый диапазон сопротивления. При этом индикатор укажет на выбранную шкалу (шкала 0 –10 – линейный режим работы, а шкалы 1 – 3 и 3 – 10 – обратно пропорциональный режим работы). Значения сопротивлений занесите в табл. 1.

3. Измерять величины исследуемых сопротивлений необходимо при комнатной температуре. Внимание! Кнопками выбора температуры отключить нагрев образца (индикатор должен показать «OFF»).

4. Рассчитайте значения удельных сопротивлений материалов по формуле (1) (исследуемые материалы рассматривать в виде проволок, намотанных на катушки с известными геометрическими параметрами S и l). Результаты занесите в таблицу 2.

Таблица 2

№

Проводящий материал

R20,Ом

r, Ом м

5. Снимите зависимость R от температуры Т. Для этого установите требуемое значение температуры термокамеры. Измерения сопротивлений производите по следующему температурному ряду: комнатная, 40, 60, 80, 100⁰С. Рекомендуется соблюдать интервал между измерениями 10 мин для стабилизации показаний прибора при нагреве образца. Результаты представьте в виде таблицы:

Таблица 3

№

Т, К

R, Ом

αR, К^-1

6. Постройте график зависимости R(Т). График зависимости R(T) аппроксимировать линейной зависимостью. Из коэффициента аппроксимации, определяющего наклон характеристики, рассчитать TKR (α_R).

7. По полученным результатам определите температурные коэффициенты сопротивления α_r для исследуемых материалов. Вычисление α_R проводите по выражению (3).

Контрольные вопросы

1. Почему удельное сопротивление металлов растет с повышением температуры?

2. Что является основными электрическими характеристиками проводников?

3. Что называют температурным коэффициентом удельного сопротивления? Является ли он константой для данного металла?

4. Как влияют примеси на удельное сопротивление металлов? Сформулируйте правило Маттиссена.

5. Почему металлические сплавы типа твердых растворов обладают более высоким удельным сопротивлением, нежели чистые компоненты, образующие сплав?

6. Какие металлы относятся к тугоплавким и почему?

7. Что собой представляют сплавы константан и нихром?

Литература

1. Физика твердого тела. Лабораторный практикум. Под ред. А.Ф. Хохлова, Том 2. Физические свойства твердых тел: Учебное пособие. - М.: Высшая школа, 2001 . – 484 С.

2. Пасынков В.В., Сорокин В.С. Материалы электронной техники: Учебник. - СПб.: Изд. «Лань», 2002. - 368 С.

3. Материаловедение. Конструкционные и электротехнические материалы. Материалы и элементы электронной техники . Практикум к лабораторным работам : учеб.-метод. пособие/ И.Л. Новиков, Р.П. Дикарева, Т.С. Романова. – Новосибирск : Изд-во НГТУ, 2010. – 56 С.

Лабораторная работа №5

Исследование сегнетоэлектриков.

Цель работы: Изучение основных электрических свойств сегнетоэлектриков и их зависимости от напряженности электрического поля.

Требуемое оборудование: 1. Измеритель электропроводности ЛСМ1 – 1 шт.

2. Стенд С3-РМ02– 1 шт.

Теория

Порядок выполнения работы

Контрольные вопросы

Литература

Теория

Активными называют диэлектрики, свойствами которых можно управлять с помощью внешних воздействий и использовать эти воздействия для создания функциональных элементов электроники. Активные диэлектрики позволяют осуществить генерацию, усиление, модуляцию электрических и оптических сигналов, запоминание или преобразование информации. К числу активных диэлектриков относятся и сегнетоэлектрики.

Сегнетоэлектриками называют вещества, обладающие спонтанной поляризацией, направление которой может быть изменено с помощью внешнего электрического поля.

В отсутствие внешнего электрического поля сегнетоэлектрики, как правило, имеют доменную структуру. Спонтанная поляризация сегнетоэлектриков обусловлена наличием доменной структуры. Домены представляют макроскопические области, обладающие спонтанной поляризацией, возникновение которой обусловлено внутренними процессами, происходящими в диэлектрике. Направление электрических моментов у разных доменов различно. Поэтому суммарная поляризованность образца в целом может быть равна нулю. Разбиение на домены уменьшает электростатическую энергию сегнетоэлектрика.

Возникновение поляризованного состояния в сегнетоэлектриках обусловлено силами различной природы. Во - первых, это силы близкодействия – обменные силы; во - вторых, силы дальнодействия – силы диполь - дипольного взаимодействия. Вклад в поляризацию диэлектрика может вносить электронная, ионная и ориентационная поляризация.

Спонтанная поляризация P_СП существует только в определенном температурном интервале, когда сегнетоэлектрик имеет доменную структуру.

При температуре фазового перехода, называемой температурой Кюри Т_К, происходит изменение структуры кристалла, сопровождаемое возникновением (исчезновением) спонтанной поляризации. При Т > Т_К исчезает электрическая асимметрия элементарной ячейки, пропадает дипольный момент и домены распадаются. В области фазового перехода резко меняются и имеют аномалии почти все свойства кристалла: электрические, оптические, механические и др.

В точке Кюри спонтанная поляризованность исчезает, а диэлектрическая проницаемость достигает своего максимального значения. Переход сегнетоэлектрика в параэлектрическое состояние сопровождается резким уменьшением tgd , поскольку исчезают потери на гистерезис.

При воздействии внешнего электрического поля электрические моменты доменов ориентируются вдоль поля, создавая наряду с электронной и ионной поляризацией еще один вид – доменную поляризацию. Эта поляризация преобладает над другими механизмами. При Т > Т_К домены исчезают и в сегнетоэлектрике наблюдаются только ионная и электронная поляризации. Закон, описывающий поведение диэлектрической проницаемости сегнетоэлектрика от температуры в области Т > Т_К, называется законом Кюри - Вейсса и имеет вид:

(1)

где С – постоянная Кюри, характеризующая материал, Т – температура в К, Т_К – температура Кюри, также измеренная в К.

Считается, что температура фазового перехода соответствует максимуму диэлектрической проницаемости. На рис. 1 представлен график зависимости e = f(t) для наиболее распространенного сегнетоэлектрика ионного типа (титанат бария BaTiO3).

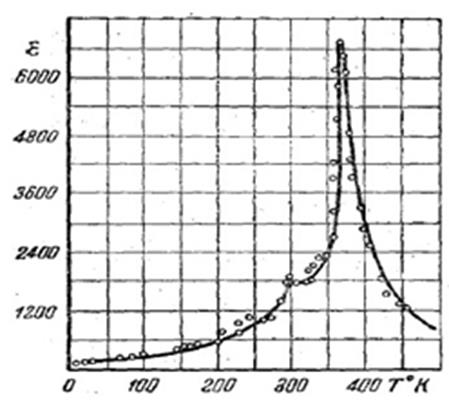
Рис.1. График зависимости e = f(t) для наиболее распространенного сегнетоэлектрика ионного типа титанат бария BaTiO₃.

Особенности сегнетоэлектриков состоят в следующем:

1. Наличие диэлектрического гистерезиса – отставание поляризации от величины приложенного внешнего поля.

При небольших значениях внешнего поля, пока оно не в состоянии переориентировать ни один из доменов, сегнетоэлектрик ведет себя как обычный диэлектрик. Но при некотором значении внешнего поля электрические моменты доменов начинают ориентироваться по полю. По мере увеличения внешнего поля начинается быстрый рост поляризации образца, как за счет движения доменных стенок, так и за счет поворота электрических моментов доменов. При достижении состояния, называемым насыщением, вектора поляризации в доменах ориентированы вдоль направления поля. Сегнетоэлектрик становится однодоменным. При дальнейшем увеличении напряженности внешнего поля общая поляризация такого кристалла слабо растет за счет увеличения индуцированной поляризации.

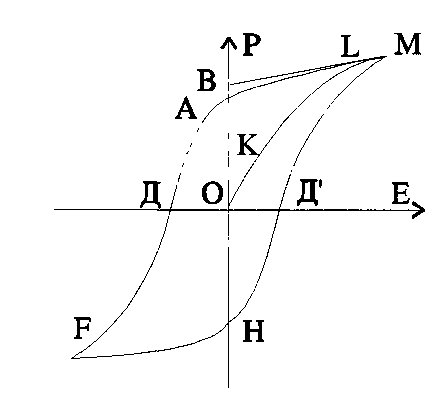
Рис.2. Петля гистерезиса для сегнетоэлектрика.

Под влиянием внешнего электрического поля в многодоменном кристалле происходит как переориентация отдельных доменов, так и увеличение поляризации каждого домена. Слабое электрическое поле, которое не в состоянии переориентировать ни один из доменов, приведет лишь к появлению индуцированной поляризации кристалла, которая линейно связана с Е, т.е. кристалл будет вести себя как обычный диэлектрик.

Это соответствует участку ОК на графике зависимости поляризации Р от напряженности электрического поля Е (рис.2).

При увеличении Е поляризация будет расти за счет переориентации отдельных доменов. При некоторой напряженности поля, соответствующей точке L, все домены ориентированы по полю. Это состояние называется состоянием насыщения; кристалл при этом состоит из одного домена, а общая поляризация такого кристалла при дальнейшем возрастании поля может расти только за счет индуцированной (т.е. электронной и ионной) поляризации. Это соответствует участку LM на рис. 2.

Уменьшение напряженности электрического поля приведет теперь к изменению поляризации по кривой MLA, когда поле будет уменьшено до нуля, некоторые домены окажутся все же ориентированными, причем кристалл будет обнаруживать остаточную поляризацию Р_ост (величина ОА на рис.2). Экстраполяция линейного участка LM до пересечения с осью Р дает величину спонтанной поляризации Р_r (величина ОВ). Чтобы полностью деполяризовать кристалл, необходимо приложить электрическое поле E_C (отрезок ОD) в противоположном направлении. Напряженность поля, при которой поляризация сегнетоэлектрика становится равной нулю, называется коэрцитивным полем (коэрцитивной силой) E_С.

Таким образом, соотношение между и описывается кривой на рис.2. Подобное необратимое изменение некоторых физических свойств под влиянием определенных процессов носит название явления гистерезиса, а соответствующая кривая на рис.2. называется петлей гистерезиса. Аналогия с известной ферромагнитной петлей гистерезиса, описывающей связь между магнитной индукцией и магнитным полем , очевидна. Это явилось причиной использования термина «ферроэлектричества» для описания сегнетоэлектриков.

Диэлектрический гистерезис обусловлен необратимым смещением доменных границ под действием поля и свидетельствует о дополнительном механизме диэлектрических потерь, связанных с затратами энергии на ориентацию доменов. Площадь гистерезисной петли пропорциональна энергии, рассеиваемой в диэлектрике за один период. Вследствие потерь на гистерезис сегнетоэлектрики характеризуются весьма большим тангенсом угла диэлектрических потерь, который в типичных случаях принимает значение порядка 0,1.

Гистерезис можно наблюдать, подводя к образцу сегнетоэлектрика с металлизированными поверхностями (сегнетоконденсатору) переменное напряжение. Часть электрической энергии, которая при переменном напряжении в диэлектрике переходит в тепло, называют диэлектрическими потерями. Площадь петли гистерезиса пропорциональна энергии, рассеянной за один период.

Изменяя значения подаваемого напряжения, можно получить семейство петель гистерезиса и восстановить кривую первоначальной поляризации. Сняв параметры петли, можно рассчитать такие характеристики сегнетоэлектрика как поляризация насыщения, остаточная поляризация, коэрцитивная сила при определенных значениях внешнего напряжения.

2. Нелинейная зависимость значения вектора поляризации P и диэлектрической проницаемости e от напряженности внешнего электрического поля.

3. Значительная зависимость диэлектрической проницаемости e от температуры с аномально большим максимумом при температуре Кюри. После температуры Кюри e резко уменьшается до значений, обусловленных индуцированной поляризацией.

4. Высокое значение e (10³..10⁴). Это обусловлено тем, что под воздействием внешнего электрического поля ориентируются электрические моменты доменов, а не отдельных атомов или молекул.

5. При переходе через точку Кюри скачкообразно изменяется целый ряд свойств вещества: структура кристаллической решетки, удельная теплоемкость, показатель преломления и др.

Исследуемый в работе сегнетоэлектрический кристалл – титанат бария, BaTiO₃, имеет несколько (кристаллических) модификаций. В параэлектрическом состоянии титанат бария обладает кубической структурой (тип перовскит). Элементарная ячейка перовскитной решетки показана на рис.3.

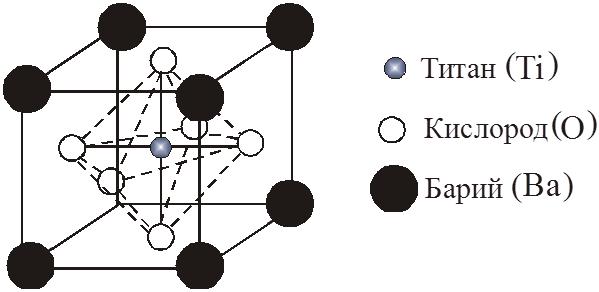
Рис.3. Элементарная кристаллическая ячейка BaTiO₃.

В центре куба расположен атом Ti, в вершинах – атомы Ba, а в центре каждой грани – атомы О. Параметр каждой ячейки равен приблизительно . При таком расположении атомов в элементарной ячейке равен нулю. Таким образом, эта фаза кристалла является неполярной фазой.

При температуре несколько выше 100°С в кристалле BaTiO₃ происходит фазовый переход, и структура становится тетрагональной. Тетрагональная элементарная ячейка получается в результате следующего искажения кубической ячейки: одно ребро куба удлиняется и становится тетрагональной осью; два других ребра сокращаются, но остаются равными друг другу по размерам.

При температуре Кюри в титанате бария происходят смещения ионов (в основном Ti) из первоначальных положений, в результате которых образуются дипольные моменты, параллельные друг другу. Таким образом, спонтанная поляризация в значительной своей части обусловлена поляризацией ионного характера.

В настоящее время известно значительное число сегнетоэлектриков, отличающихся химическим составом, кристаллической структурой и свойствами. По механизму возникновения спонтанной поляризации все сегнетоэлектрики можно разделить на две группы.

1-я группа – возникновение Р_СП обусловлено упорядочением определенных элементов структуры (например, водородных связей). Сюда относятся сегнетова соль и другие дополнительные сегнетоэлектрики.

2-я группа – возникновение Р_СП связано со смещением некоторых ионов, занимавших в структуре центросимметричное положение при температуре выше Кюри. Сюда относятся титанаты и аналогичные им вещества – это ионные сегнетоэлектрики.

Сегнетоэлектрики используются для изготовления нелинейных конденсаторов (сегнетокерамика типа ВК-1, ВК-2, ВК-3, ВК-4). Такие конденсаторы - вариконды применяются в различных схемах, где нужна нелинейность: для умножения и деления частоты; для детектирования сигналов; для создания частоты модуляции в схемах реле времени; в ячейках памяти; для создания диэлектрических усилителей и других устройств. В качестве материалов для варикондов чаще всего выступают твердые растворы систем Ba(Ti, Sn)O₃, Pb(Ti,Zr,Sn)O₃. Использование твердых растворов в системе сегнетоэлектрика позволяет варьировать основные параметры материала в широких пределах.

Методика проведения эксперимента

Свойства сегнетоэлектриков исследуются с помощью характериометра ИСХ1 (рис. 4а), работающего совместно со стендом С3-РМ02 (рис. 4б).

а) б)

Рис.4. Измерительная установка.

Порядок работы с прибором

1. Для включения прибора нажмите кнопку «Сеть», при этом загорится индикатор. Прогрейте прибор 5 мин.

2. Регулировка контраста изображения проводится вращением ручки «КОНТРАСТ».

3. Соберите электрическую схему.

4. Для переключения режима работы нажмите кнопку «F». При этом должен подсветиться текущий режим работы. Затем кнопками «+» или «–» выберите необходимый режим:

I=F(U1) (вольт-амперная характеристика);

U2=F(U1) (статическая характеристика);

U2=F(I) (передаточная характеристика).

5. Установите требуемый сигнал на выходе генератора. Для этого одиночным нажатием кнопки «Генер.» подсветите строку «ФОРМА» и кнопками «+» и «–» выберите необходимую форму сигнала (синусоидальная, треугольная). В работе используется синусоидальная форма сигнала. Повторным. нажатием кнопки «Генер.» подсветите строку «АМПЛ.» и кнопками «+» и «–» установите необходимую амплитуду выходного сигнала (в вольтах).

6. Для изменения коэффициента отклонения нажмите кнопку «Усил.». При этом подсветится надпись «УСИЛ.» того канала, который соответствует выбранному режиму работы. Если режим работы предполагает совместное использование двух каналов, то переход между выбором коэффициентов отклонения каналов осуществляется повторным нажатием кнопки «Усил.». Установить необходимое значение коэффициента отклонения для выбранного канала можно при помощи кнопок «+» или «–».

Для включения режима «Стоп - кадр» необходимо нажать кнопку «СТОП». При этом кадр будет остановлен для проведения измерений. Для выхода из этого режима необходимо нажать кнопку «СТОП» повторно.

8. Установка требуемой температуры (по умолчанию образцы имеют температуру окружающей среды) осуществляется нажатием кнопки «ТЕМПЕРАТУРА» и последующим выбором кнопками «+» и «–» температуры, до которой необходимо нагреть образцы. В строке «УСТАН.» отображается заданная температура, а в строке «ТЕКУЩ.» ее текущее значение. Для регулировки температуры сегнетоэлектрика стенд снабжен вентилятором.

Градуировка горизонтальной и вертикальной осей характериографа

После включения установки ИСХ1, используя соединительные провода, необходимо подключить стенд С3 - РМ02 к измерительным клеммам прибора. Для этого сигнал с генератора подается на первичную обмотку повышающего трансформатора, а выходной сигнал U2 снимается с эталонного конденсатора С₁, так как напряжение на нем пропорционально его заряду (и заряду на конденсаторе С₂, так как при последовательном включении конденсаторов их заряды равны). При этом на горизонтальный вход осциллографа подается напряжение с резистора R₁, которое связано с общим падением напряжения во второй обмотке U следующим образом: U = U1(1+R₂/R₁). Таким образом, по горизонтальной оси осциллограммы откладывается значение напряжения, а по вертикальной – значения заряда.

Масштабный коэффициент для горизонтальной оси вычисляется (оси напряжений) по формуле:

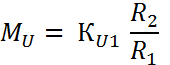
где К_U1 – показания коэффициента усиления сигнала по входу U1 (В/дел);

Масштабный коэффициент для горизонтальной оси вычисляется (оси зарядов) по формуле:

где К_U2 – показания коэффициента усиления сигнала по входу U2 (В/дел).

Порядок выполнения работы

1. Определение основных параметров петли гистерезиса.

Определение основных параметров петли гистерезиса проводится при максимальном ее (предельном) размере. Для получения максимального размаха петли необходимо установить максимальное значение напряжения U_ген = 10 В. После этого определить максимальный заряд q_max, остаточный заряд q_r и коэрцитивную силу U_С (см. рис. 3). Данные занести в таблицу.

Таблица 1

Xmax

Ymax

Qmax

XR

YR

QR

XC

YC

EC

2. Построение основной кулон - вольтной кривой сегнетоконденсатора.

При помощи генератора сигнала постепенно увеличивают напряжение U_ген от нуля до 10 В ступенями 1 В. На экране характериографа получаются все увеличивающиеся петли гистерезиса. При этом каждый раз фиксируется координаты положительной вершины петли, т.е. координаты амплитудных значений заряда q_m и напряжения U_m. Кривая, соединяющая вершины петель, есть основная кулон - вольтная кривая. Для ее построения удобно использовать режим «СТОП - кадр».

Примечание. Для более точного определения координат вершин при малых значениях U_ген, изменяйте коэффициенты усиления по осям K_U1, K_U2, чтобы размер кривой был больше 5 мм х 5 мм.

3. Определение температуры Кюри

Для определения температуры Кюри установите напряжение генератора 10 В. Определите X и Y - координаты положительной вершины предельной петли гистерезиса. Установите последовательно следующий температурный ряд: 30, 40, 60, 65, 70, 75 ⁰С. Интервал между измерениями 3 мин. Для каждой температуры фиксируйте Y - координату вершины петли гистерезиса. По результатам измерений постройте зависимость ε_эф = f(Т) и определите из графика температуру Кюри, как точку максимальной величины диэлектрической проницаемости

Контрольные вопросы

1. Что такое сегнетоэлектрики? Какая электрическая упорядоченность свойственна сегнетоэлектрикам?

2. К каким диэлектрикам относятся сенгнетоэлектрики и почему?

3. Как объяснить диэлектрический гистерезис и нелинейность зависимости заряда от напряжения у сегнетоэлектриков?

4. Что называется сегнетоэлектрической точкой Кюри?

5. Каков микроскопический механизм спонтанной поляризации титаната бария?

6. Типы сегнетоэлектриков и их применение.

Литература

1. Пасынков В.В., Сорокин В.С. Материалы электронной техники: Учебник. - СПб.: Изд.«Лань», 2002. - 368 С.

2. Материаловедение. Конструкционные и электротехнические материалы. Материалы и элементы электронной техники. Методические указания к лабораторным работам №1-4 для студентов II курса ЭМФ, РЭФ/В.Н. Гаревский И.Л. Новиков, Р.П. Дикарева, Т.С. Романова. – Новосибирск : Изд-во НГТУ, 2009. – 74 С.

Лабораторная работа №6

Исследование диэлектрической проницаемости и диэлектрических потерь в твердых диэлектриках.

Цель работы: Определить зависимость диэлектрической проницаемости и диэлектрических потерь в твердых диэлектриках от температуры.

Требуемое оборудование: 1. Измеритель электропроводности ЛСМ1 – 1 шт.

2. Измерительные кассеты– 3 шт.

Теория

Порядок выполнения работы

Контрольные вопросы

Литература

Теория

Характерным для любого диэлектрика процессом, возникающим при воздействии на него электрического напряжения, является поляризация – ограниченное смещение связанных зарядов или ориентация дипольных молекул.

Поляризацией называется состояние диэлектрика, характеризующееся наличием электрического момента у любого элемента его объема.

Различают поляризацию, возникающую под действием внешнего электрического поля (наведенную или индуцированную), и спонтанную (самопроизвольную), существующую в отсутствии поля.

О явлениях, обусловленных поляризацией диэлектриков, можно судить по значению диэлектрической проницаемости, а также по величине диэлектрических потерь, если поляризация диэлектрика сопровождается рассеянием энергии.

Способность различных материалов поляризоваться в электрическом поле характеризуется диэлектрической проницаемостью e:

, (1)

где С_Д – емкость конденсатора с данным диэлектриком, С₀ – емкость того же конденсатора, если бы между электродами находился вакуум.

Величина относительной диэлектрической проницаемости является безразмерной величиной.

Количественной характеристикой поляризации является поляризованность диэлектрика P. Поляризованностью называют векторную физическую величину, равную отношению электрического момента dp элемента диэлектрика к объему dV этого элемента

(2)

Рассматривая явления поляризации с учетом агрегатного состояния и структуры диэлектрика, следует различать следующие механизмы поляризации: электронный, ионный, дипольно – релаксационный, электронно – релаксационный, ионно – релаксационный, резонансный , миграционный и спонтанный.

К мгновенным видам поляризации относятся механизмы, протекающая в диэлектрике под воздействием электрического поля практически мгновенно, вполне упруго, без рассеяния энергии. К этому виду относятся электронная и ионная поляризации. Время установления этих механизмов ничтожно мало (~ 10^-13 - 10^-15 с).

К замедленным механизмам относятся те, когда поляризация нарастает и убывает замедленно, и сопровождается рассеянием энергии в диэлектрике, т. е. нагревом. Поляризация такого вида называется релаксационной. К этому виду относятся дипольно - релаксационная, ионно - релаксационная и электронно - релаксационная, а также миграционная поляризация, возникающая в твердых диэлектриках неоднородной структуры.

В зависимости от влияния напряженности внешнего электрического поля на величину диэлектрической проницаемости материала все диэлектрики делятся на линейные (рис.1а) и нелинейные (рис.1б).

а)

б)

Рис.1. Зависимость диэлектрической проницаемости от напряженности электрического поля для линейных (1а) и нелинейных (1б) диэлектриков.

Линейные диэлектрики относят к пассивным диэлектрикам, применяемым в основном в качестве различных видов электрической изоляции или диэлектрика конденсаторов.

Нелинейные диэлектрики относят к активным диэлектрикам, параметры которых зависят от величины приложенной разности потенциалов. Емкостью конденсатора с нелинейным диэлектриком можно управлять электрическим полем.

В диэлектрике, помещенном в переменное электрическое поле, происходит некоторое выделение энергии. Диэлектрическими потерями называют энергию, рассеиваемую в единицу времени в диэлектрике при воздействии на него электрического поля и вызывающую нагрев диэлектрика.

Если бы в диэлектрике конденсатора мощность совсем не рассеивалась («идеальный диэлектрик»), то вектор тока I опережал бы вектор напряжения U точно на 90⁰, а ток был бы чисто реактивным I_С. Но в реальном диэлектрике наряду с реактивным током имеет место ток активный (ток потерь). Таким образом, полный ток, складывающийся из двух токов (активного и реактивного), опережает напряжение на угол j, несколько меньший 90⁰, т.е. величина угла j связана с величиной активного тока (тока потерь). Чем больше Ia, тем сильнее угол j отклоняется от 90⁰. Но в качестве характеристики потерь взят не сам угол j, а угол δ, дополняющий угол j до 90⁰ , т.е. δ = 90 – j.

Угол δ называют углом диэлектрических потерь. Чем больше этот угол, тем больше (при прочих равных условиях) диэлектрические потери.

Обычно в качестве параметра материала дают величину тангенса угла потерь. Очевидно, что тангенс угла потерь равен отношению активного и реактивного токов:

(3)

Легко получить выражение для величины диэлектрических потерь Р в участке изоляции, обладающем емкостью С. Очевидно, что

. (4)

С учетом того, что значение силы тока через участок изоляции с емкостью С равно:

где – угловая частота, получим:

(5)

Диэлектрические потери по их особенностям и физической природе делятся на четыре основных вида.

1. Потери на электропроводность.

2. Релаксационные потери.

3. Ионизационные потери.

4. Резонансные потери.

Диэлектрики, построенные из неполярных молекул (полиэтилен, полистирол) и обладающие только электронной поляризацией, имеют наименьшее значение диэлектрической проницаемости. Температурная зависимость диэлектрической проницаемости неполярных диэлектриков определяется изменением числа молекул в единице объема. В диэлектриках, обладающих электронной поляризацией, диэлектрические потери невелики и обусловлены, как правило, только сквозной электропроводностью и наличием примесей.

Величина тангенса угла диэлектрических потерь может быть вычислена по следующей формуле

(6)

где f – частота приложенного напряжения, Гц; r – удельное сопротивление диэлектрика.

Диэлектрические потери, обусловленные электропроводностью, возрастают с температурой по экспоненциальному закону вида

(7)

где А, b – const.

Диэлектрики, представляющие собой ионные кристаллы с плотной упаковкой частиц, обладают ионной и электронной поляризацией и имеют величину диэлектрической проницаемости, лежащую в широких пределах. Температурный коэффициент диэлектрической проницаемости ионных кристаллов в большинстве случаев имеет положительное значение, вследствие того что при повышении температуры наблюдается не только уменьшение плотности вещества, но и возрастание поляризуемости кристаллической решетки, причем влияние этого фактора сказывается на величине температурного коэффициента сильнее, чем изменение плотности

В кристаллических структурах с плотной упаковкой ионов (слюда, кварц) при отсутствии примесей, искажающих решетку, диэлектрические потери весьма малы. При повышенных температурах в таких веществах появляются потери от электропроводности. В диэлектриках ионной структуры с неплотной упаковкой ионов (электротехнический фарфор) наблюдаются также потери, связанные с релаксационной поляризацией.

У диэлектриков с дипольными молекулами (поливинилхлорид, полиамиды, материалы на основе целлюлозы) зависимость от температуры проявляется значительно резче и характеризуется наличием максимума. В низкотемпературной области ориентация молекул в большинстве случаев невозможна из-за значительной вязкости. При повышении температуры ориентация диполей облегчается, что приводит к возрастанию диэлектрической проницаемости.

Исследуемые образцы

В данной работе для исследования используются образцы гетинакса, текстолита и стеклотекстолита, относящиеся к слоистым пластикам.

Слоистые пластики - это разновидность пластмасс, где связующим веществом служит полимер, а наполнителем – листовые волокнистые материалы. Наиболее широкое применение получили: стеклотекстолит, гетинакс и текстолит.

Гетинакс – листовой слоистый прессованный материал, состоящий из двух или более слоев бумаги, пропитанной термореактивной смолой. Электротехнический гетинакс выпускают восьми марок. В зависимости от марки в качестве связующего вещества применяют фенолформальдегидные смолы или эпоксидную смолу типа ЭД - 16. Гетинакс является анизотропным материалом, поэтому электрическая прочность гетинакса вдоль слоев в 5 - 8 раз ниже, чем поперек, а удельное сопротивление ниже в 50 - 100 раз. Гетинакс легко обрабатывается механически, а тонколистовые сорта хорошо штампуются, особенно в подогретом состоянии. Из гетинакса изготовляют детали радиотехнического и электротехнического назначения. Гетинакс используется для изготовления наиболее дешевых печатных плат.

Стеклотекстолит – слоистый прессованный материал, состоящий из двух или более слоев стеклоткани, пропитанной различными термореактивными связующими. Производят следующие марки: СТ - Б, СТ -1 на основе фенолоформальдегидной смолы; СТЭФ - 1 и СТЭФ - Р на эпоксидно - феноловом связующем; СТК - на кремнийорганическом связующем. Стеклотекстолит обладает повышенной влагостойкостью и лучшими электрическими и механическими параметрами по сравнению с текстолитом и гетинаксом, но хуже обрабатывается механически. Из стеклотекстолита изготовляют платы печатных схем, антенные обтекатели и другие радиодетали.

Текстолит – слоистый пластик, в котором в качестве наполнителя используют хлопчатобумажную ткань, пропитанную термореактивной смолой фенолформальдегидного типа. Выпускают четырех марок: А, Б, Г – на основе сравнительно грубых тканей – бязи и миткаля, и ВЧ (для высоких частот) – на основе шифона.

Дороже гетинакса, так как стоимость ткани значительно дороже стоимости бумаги. Листовой текстолит применяют как конструкционно-изоляционный материал для изделий, подвергающихся ударным нагрузкам или работающих на истирание (детали переключателей).

Методика проведения эксперимента

В настоящей работе используется измеритель индуктивности и емкости ЛСМ1 (рис. 2). С его помощью можно определить емкость конденсатора, индуктивность катушек, а также тангенс угла потерь.

Для включения прибора необходимо нажать кнопку «Сеть», при этом на передней панели загорится ряд индикаторов «Шкала», «Температура», «Канал», «С» и т.д.

Рис.2. Измеритель индуктивности и емкости ЛСМ1.

Исследуемые образцы находятся в измерительной кассете ИК1. Для ее установки в прибор необходимо поднять шторку, установить кассету с образцами в термокамеру прибора до упора. При этом шторка должна опуститься.

Затем установите требуемый режим измерения (емкость C или тангенс угла потерь tg d). Выберите требуемый диапазон измерений.

Установите требуемое значение температуры термокамеры. При первом нажатии кнопки на индикаторе «Температура» высветится установленное значение температуры. При повторном нажатии кнопки произойдет коррекция устанавливаемой температуры. Через 2 с после завершения установки индикатор «Температура» перейдет в режим отображения текущей температуры. Для отключения терморегулятора необходимо установить температуру менее 30⁰ С. При этом на экране высветится сообщение «OFF».

Сообщения, выдаваемые прибором

При работе прибора на индикаторе могут отображаться следующие сообщения:

· L – измеряемая величина C ниже выбранного диапазона;

· H – измеряемая величина C выше выбранного диапазона;

· P – измеряемое значение тангенса потерь C выше выбранного диапазона;

· A – при измерении активная составляющая больше реактивной (tgδ>1).

Зная величину емкости конденсатора, его геометрическую форму и размеры, можно вычислить величину диэлектрической проницаемости диэлектрика конденсатора.

(8)

где h – толщина образца S – площадь верхнего электрода; e₀ = 8,85 10^-12 Ф/м.

Размеры образцов: Стеклотекстолит СТ – 4 - h = 4 мм, S = 60 х 60 мм; Текстолит – h = 2 мм; S = 60 х 60 мм; Гетинакс - h = 2 мм; S = 60 х 60 мм.

Порядок выполнения работы

1. Установите картридж с образцом в прибор. При комнатной температуре измерьте С и tgδ диэлектрика на фиксированной частоте при комнатной температуре. Для этого установите требуемый канал для измерения. И выберите диапазон измерения С и tgδ. По полученным результатам измерения рассчитать значение e.

2. Провести измерение температурной зависимости e = f(T). Для этого установите требуемое значение температуры термокамеры. Измерения С и tgδ производите по следующему температурному ряду: комнатная, 40, 60, 80, 100⁰ C. Рекомендуется соблюдать интервал между измерениями 10 мин для стабилизации показаний прибора при нагреве образца. По полученным значениям рассчитать e. По окони измерений отключите терморегулятор. Для этого необходимо установить температуру менее 30⁰ С. При этом на экране высветится сообщение «OFF». Осторожно выньте образец из термокамеры.

3. Постройте график зависимости e = f(T). Для тангенса угла диэлектрических потерь tgδ построить зависимость ln(tgδ) = f(1/T). Выполнив линейную аппроксимацию экспериментальных точек, по тангенсу угла наклона определить эффективную энергию активации носителей заряда по формуле:

.

4. Результаты измерений занести в таблицу 1.

Таблица 1

№

Исследуемый материал

Т, ^0С

С, Ф

tg d

e

Контрольные вопросы

1. Поляризация. Типы поляризации.

2. Какие виды поляризации можно отнести к замедленным и почему?

3. Линейные и нелинейные, полярные и неполярные диэлектрики.

4. Что называется диэлектрической проницаемостью?

5. Диэлектрические потери. Виды диэлектрических потерь.

6. Каков физический смысл параметра tg d.

7. Охарактеризуйте исследуемые в работе диэлектрики. Справедливо ли утверждение, что они являются активными диэлектриками?

Литература

1. Пасынков В.В., Сорокин В.С. Материалы электронной техники: Учебник. - СПб.: Изд.«Лань», 2002. - 368 С.

2. Материаловедение. Конструкционные и электротехнические материалы. Материалы и элементы электронной техники . Методические указания к лабораторным работам №1-4 для студентов II курса ЭМФ, РЭФ/В.Н. Гаревский И.Л. Новиков, Р.П. Дикарева, Т.С. Романова. – Новосибирск : Изд-во НГТУ, 2009. – 74 С.

Лабораторная работа №7

Исследование влияния магнитного поля на удельное сопротивление полупроводника.

Цель работы: изучение зависимости сопротивления полупроводника от внешнего магнитного поля. Измерения проводятся при постоянном магнитном поле на образцах германия.

Теория

Порядок выполнения работы

Контрольные вопросы

Литература

Теория

Магнетосопротивление (магниторезистивный эффект) — изменение электрического сопротивления материала в магнитном поле. Впервые эффект был обнаружен в 1856 г. Уильямом Томсоном. В общем случае можно говорить о любом изменении тока через образец при том же приложенном напряжении и изменении магнитного поля. Все вещества в той или иной мере обладают магнетосопротивлением. Для сверхпроводников, способных без сопротивления проводить электрический ток, существует критическое магнитное поле, которое разрушает этот эффект и вещество переходит в нормальное состояние, в котором наблюдается сопротивление. В нормальных металлах эффект магнетосопротивления выражен слабее. В полупроводниках относительное изменение сопротивления может быть в 100 - 10 000 раз больше, чем в металлах, и может достигать сотен тысяч процентов.

Магнетосопротивление вещества зависит и от ориентации образца относительно магнитного поля. Это связано с тем, что магнитное поле не изменяет проекцию скорости частиц на направление магнитного поля, но благодаря силе Лоренца закручивает траектории в плоскости, перпендикулярной магнитному полю. Это объясняет, почему поперечное поле действует сильнее продольного. Здесь речь пойдёт в основном о поперечном магнетосопротивлении двумерных систем, когда магнитное поле ориентировано перпендикулярно к плоскости движения частиц.

На основе магниторезистивного эффекта создают датчики магнитного поля.

Магниторезистивный эффект

В полупроводнике, помещенном в магнитное поле, при прохождении электрического тока на носители действует сила Лоренца,

(1)

где - индукция магнитного поля; - дрейфовая скорость носителей заряда, e - заряд электрона. Если в полупроводнике один из носителей, то в нем возникает поперечное электрическое поле - поле Холла. Напряженность этого поля такова, чтобы его сила точно скомпенсировала действие на носители силы Лоренца: линии тока должны быть параллельны граням образца.

Однако скорости движения носителей неодинаковы из-за теплового размытия, поэтому поле Холла компенсирует действие силы Лоренца только для носителей, движущихся со средней скоростью. На более медленные носители сильнее действует поле Холла, а на более быстрые — сила Лоренца. Поэтому вклад в проводимость носителей, движущихся со скоростью, отличной от средней, в магнитном поле оказывается меньше. Уменьшение проводимости полупроводника в магнитном поле называется эффектом Гаусса или магниторезистивным эффектом (магнетосопротивление). В полупроводнике с двумя видами носителей поле Холла меньше, поэтому линии тока в нем непараллельны граням и эффект магнетосопротивления соответственно больше.

Под действием силы Лоренца траектория движения носителя заряда искривляется, что равносильно уменьшению длины свободного пробега в направлении внешнего поля между токовыми контактами или увеличению удельного сопротивления полупроводника в магнитном поле.

Для наблюдения эффекта Холла удобно использовать пластинку полупроводника, помещенную в магнитное поле. В этом случае при установлении динамического равновесия возникшая холловская напряженность электрического поля компенсирует действие силы Лоренца и, следовательно, не происходит искривления траекторий носителей заряда, движущихся со скоростью v. Казалось бы, в таком случае сопротивление полупроводника не должно изменяться под действием магнитного поля. Однако эти рассуждения справедливы только для носителей, движущихся со скоростью v , соответствующей средней скорости. В действительности же, как было отмечено, носители в полупроводнике распределены по скоростям. Поэтому носители со скоростью, превышающей среднюю скорость, смещаются к одной грани пластинки полупроводника, так как на них действует большая сила Лоренца. Носители, обладающие скоростью, меньшей средней скорости, смещаются к другой грани пластинки полупроводника, так как на них действует большая сила холловской напряженности электрического поля. Таким образом, в рассмотренном примере удельное сопротивление полупроводника изменяется в магнитном поле из-за искривления траекторий носителей заряда, движущихся со скоростью, отличной от средней скорости.

Холловская напряженность электрического поля частично или полностью компенсирует действие силы Лоренца в зависимости от скорости носителей заряда. Поэтому наибольший магниторезистивный эффект можно получить в полупроводнике таких формы и конструкции, при которых возникновение холловской напряженности электрического поля будет затруднено или вообще невозможно. Теоретически такую конструкцию можно представить, если предположить неограниченность полупроводниковой пластинки в направлении, параллельном токовым контактам.

В неограниченном полупроводнике не происходит накопления носителей заряда на боковых гранях пластинки полупроводника, не образуется ЭДС Холла, а траектория движения носителей заряда отклоняется от направления внешнего электрического поля в направлении силы Лоренца (рис.1). В этом случае вектор плотности тока совпадает по направлению со скоростью движения дырок и поэтому оказывается сдвинутым от направления внешнего электрического поля на тот же угол j - угол Холла.

Рассмотрим теперь магниторезистивный эффект с количественной точки зрения при оптимальных условиях, т. е. для неограниченного полупроводника.

Отклонение траектории движения носителей заряда от направления внешнего электрического поля в неограниченном полупроводнике равносильно уменьшению длины свободного пробега носителей заряда в направлении электрического поля на

, (2)

где - длина свободного пробега носителей заряда при отсутствии магнитного поля; - проекция пути, пройденного носителем заряда между двумя последовательными столкновениями (длина свободного пробега) при наличии магнитного поля, на направление внешнего электрического поля (рис. 1).

При малых магнитных полях и, следовательно, при малых значениях угла Холла j можно воспользоваться разложением в ряд:

.

Тогда

. (3)

После возникновения холловской напряженности электрического поля и установления динамического равновесия между силой Лоренца и силой холловского электрического поля все носители заряда, имеющие скорость v, будут двигаться по прямолинейным траекториям в соответствии с направлением внешнего электрического поля Е. При этом направление вектора суммарного электрического поля () отличается от технического направления вектора тока на некоторый угол j, который называют углом Холла. Угол Холла определяют по формуле

F_Л

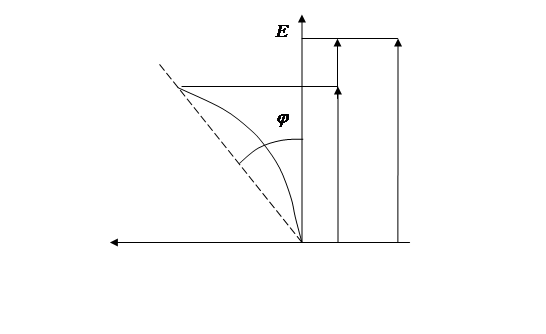
Рис. 1. Изменение длины свободного пробега носителя заряда (дырки) вдоль вектора электрического

поля в полупроводнике, находящемся в магнитном поле

Холловская напряженность электрического поля в полупроводнике с электропроводностью р - типа определяется выражением

. (5)

Напряженность в пластинке полупроводника от внешнего источника питания

(6)

Поэтому

. (7)

Очевидно, что для полупроводниковой пластинки с электропроводностью n - типа получится аналогичное соотношение между углом Холла, подвижностью электронов и значением магнитной индукции. При малых магнитных полях и, следовательно, при малых углах Холла

или

. (8)

С учетом (8), получим

. (9)

Так как за время свободного пробега носитель заряда проходит при наличии магнитного поля меньший путь вдоль электрического поля Е, то это эквивалентно уменьшению дрейфовой скорости или подвижности, а, следовательно, и удельной проводимости полупроводника. Относительное изменение удельного сопротивления при этом

(10)

Для ограниченного по размерам кристалла полупроводника обычно пользуются соотношением

, (11)

где С - коэффициент, зависящий от геометрических размеров пластинки полпроводника.

Магниторезисторы

Магниторезистор - это полупроводниковый резистор, в котором используется зависимость электрического сопротивления от магнитного поля.

Принцип действия магниторезисторов основан на магниторезистивном эффекте (см. §1). Поскольку холловская напряженность электрического поля, возникающая в полупроводнике с током при наличии магнитного поля, снижает магниторезистивный эффект, то конструкция магниторезистора должна быть такой, чтобы уменьшить или полностью устранить ЭДС Холла. Наилучшей формой магниторезистора является диск Корбино (рис. 2а).

Исключить влияние эффекта Холла можно и в полупроводнике с одним видом носителей, например, используя образцы специальной формы. Если сделать образец в виде пластинки с концентрическим расположением контактов: один в центре, а другой по окружности на равных расстояниях от первого, то ток будет протекать по радиусам. При помещении в магнитное поле, пронизывающее перпендикулярно пластину, носители будут отклоняться вдоль поверхности. Линии тока удлиняются, но накопления зарядов происходить не будет, и поле Холла не возникнет. В такой структуре, называемой диском Корбино, наблюдается максимальный эффект магнитосопротивления.

Исключить эффект Холла можно также, если на поверхность полупроводниковой пластинки нанести узкие металлические полоски для закорачивания холловской разности потенциалов. Они должны быть расположены перпендикулярно линиям тока и направлению индукции магнитного поля. Вместо нанесенных на поверхность полосок могут использоваться монокристаллы с пронизывающими их металлическими иглами. Такой вариант используется для создания магниторезисторов из InSb + NiSb. При выращивании монокристаллов из этого материала NiSb образует иглы высокой проводимости, которые при выборе соответствующей ориентации практически полностью исключают поле Холла.

В настоящее время для создания магниторезисторов наиболее широко используется антимонид индия, причем на поверхность наносятся, как правило, металлические полоски. Широко применяются магниторезисторы из упоминавшегося выше InSb + NiSb. В последнее время предложено использовать твердый раствор (HgTe)_1-x + СdТе_x. В зависимости от состава и температуры в этом твердом растворе меняется ширина запрещенной зоны и подвижность носителей. Наибольшей подвижностью обладают полупроводники с нулевой запрещенной зоной. Поскольку эффект магнитосопротивления тем больше, чем выше подвижность, то для создания магниторезисторов наиболее перспективно использование бесщелевых составов. Поэтому состав твердого раствора необходимо выбирать в зависимости от требуемой рабочей температуры. Магниточувствительность магниторезисторов из теллуридов кадмия и ртути при всех температурах получается более высокой, чем магниторезисторов из антимонида индия. Однако сопротивление образца без магнитного поля оказывается в них меньше, что несколько осложняет их практическое использование. Для повышения начального сопротивления магниторезисторы изготавливаются в виде змейки. При малых магнитных полях эффект магнитосопротивления квадратичен относительно индукции поля, а при больших становится линейным.

При отсутствии магнитного поля ток в таком магниторезисторе проходит в радиальном направлении от центра диска ко второму электроду, расположенному по периметру диска, или наоборот. Под действием магнитного поля носители заряда отклоняются в направлении, перпендикулярном радиусу. Так как не существует граней, на которых может происходить накопление зарядов, то ЭДС Холла в таком магниторезисторе не возникает.

Рис. 2. Различные конструкции магниторезисторов:

а - магниторезистор в виде диска Корбино; б — магниторезистор, изготовленный из пластинки полупроводника с малой длиной, в — магниторезистор из пластинки или пленки полупроводника с поперечными

металлическими полосками на поверхности

Другой конструкцией магниторезистора является пластинка полупроводника, ширина которой много больше ее длины (рис.2б). Однако существенным недостатком магниторезистора такой конструкции является его малое сопротивление, для увеличения которого применяют последовательное соединение нескольких магниторезисторов или нанесение на поверхность пластины полупроводника металлических полос (рис.2в). Каждая часть пластины полупроводника между двумя металлическими полосами представляет собой отдельный магниторезистор. Можно также считать, что металлические полосы выполняют роль шунтов, уменьшающих ЭДС Холла, возникающую на боковых гранях пластины полупроводника.

Основным полупроводниковым материалом для магниторезисторов является антимонид индия InSb и арсенид индия InAs - материалы с большой подвижностью носителей заряда.

Порядок выполнения работы

В работе используется стенд по физике полупроводников СФП-5, предназначенный для измерения электрофизических параметров полупроводниковых материалов и универсальная измерительная головка (УИГ), содержащая образец германия n-типа, расстояние между зондами 15 мм, размеры образца 20х3х2,5 мм. УИГ состоит из германиевого образца, на котором располагаются два миниатюрных электронагревателя. Первый служит для относительно равномерного нагрева, а второй – для создания разности температур (см. рис.6).

1 2

Т₁ Т₂

3

Рис.3. Образец для изучения магнитосопротивления с контактами.

Термопары Т₁ и Т₂ служат для определения усредненной температуры при равномерном нагреве, а также для измерения разности температур. Кроме того, один проводник термопары используется как токопроводящий при наблюдении эффекта Холла и снятии зависимости электропроводности от температуры. В первом случае ЭДС Холла снимается с 1-го и 3-го вольфрамового зондов, во втором – с 1-го и 2-го.

В работе также используется цифровой вольтметр В7 - 16 (В7 - 40), либо другой с R_вх Þ 10 мОм и пределами измерения U от 0,05 мВ до 10 В.

1. УИГ помещают между полюсными наконечниками электромагнита. К клеммам « - » и «U» панели блока управления подключается вольтметр В7-16. Через образец пропускают ток, для этого переключатель П3 устанавливают в положение «U_хол.», П2 – «Выкл.», ручками «Ток образца» устанавливают необходимое значение тока.

2. Измеряют паразитную ЭДС между холловскими зондами образца при различной полярности тока.

3. Включают электромагнит, напряженность магнитного поля которого регулируется потенциометром «Ток магнита» и измеряют значение ЭДС Холла при различных направлениях магнитного поля, полярности и величины тока образца, а также при нескольких значениях тока магнита.

4. Установить тумблер «Нагрев образца» в нейтральное положение. Измерить сопротивление R и рассчитать удельное сопротивление r в зависимости от величины напряженности магнитного поля Н. Удельное сопротивление образца германия r = 0,195 Ом м при комнатной температуре. Так как германий относится к слабо магнитным материалам, то при расчетах принять m = 1.

5. Для исключения влияния паразитной разности потенциалов, возникающей за счет несимметричного расположения поперечных зондов необходимо проводить измерения (V_X) при двух полярностях магнитного поля, меняя направление тока через обмотку электромагнита.

6. Исходя из полученных значений U_Н, и размеров образца легко рассчитать концентрацию носителей заряда

(13)

коэффициент Холла по формуле

(14)

подвижность носителей заряда

. (15)

7. Результаты занести в таблицу 1 и представить в виде графика . Рассчитать относительное изменение удельного сопротивления по формуле (10).

Таблица 1.

№ пп

IМ, А

H, эрстед

B, Тл

r, Ом см

n

m

j

Контрольные вопросы

1. Что такое сила Лоренца? Запишите формулу.

2. Что такое угол Холла и от чего он зависит?

3. Что такое магниторезистивный эффект?

4. Какую конструкцию должны иметь магниторезисторы?

5. Что такое диск Корбино?

6. Какие материалы используют для изготовления магниторезисторов?

Литература

1. Пасынков В. В., Чиркин Л. К. - Полупроводниковые приборы: Учебник для вузов. 5-е изд., испр. - СПб.: Издательство «Лань», 2001, 480 С.

2. Викулин И. Р., Стафеев В. И. - Физика полупроводниковых приборов. – 2-.е изд., перераб. и доп. - М.: Радио и связь, 1990 г., 264 С.