Написать программу вычисления выражения
Z = A
+ A-3
![]() , в котором
, в котором
Лабораторная
работа № 4
Программирование с
использованием подпрограмм
Цель работы: приобретение практических навыков реализации процедур и функций.
Используемые программные средства: Borland Delphi.
В практике программирования
часто возникают ситуации, кгда одну и ту же группу операторов, реализующих
определенную цель, требуется повторить без изменений в нескольких местах
программы. Для избавления от столь нерациональной траты времени была предложена
концепция подпрограммы, которые в языке ОР бывают двух типов: процедуры и функции.
Процедура- это независимая именованная часть программы, которую
можно вызвать по имени для выполнения определенных действий. Структура процедуры повторяет структуру программы. Процедура не может выступать в качестве операнда в
выражении. Упоминание имени процедуры в
тексте программы приводит к активизации процедуры и называется ее вызовом.
Функция сходна с процедурой, но имеет 2 отличия: функция передает в точку вызова
скалярное значение; имя функции может входить в выражение в качестве операнда.
Итак, отличие подпрограмм-процедур от
подпрограмм-функций состоит в том, что процедуры служат для задания
совокупности действий, направленных на изменение внешней по отношению к ним
программной обстановки, а функции, являясь частным случаем процедур,
обязательно возвращают в точку вызова основной программы единственный результат
как значение имени этой функции. Все процедуры и функции языка Оbject Рascal делятся на две группы:
встроенные (стандартные) и определенные пользователем. Первые входят в состав языка и вызываются для выполнения по
строго фиксированному имени. Вторые разрабатываются и именуются самим пользователем.
Для использования
стандартной процедуры или функции к программе подключается тот или иной
специализированный библиотечный модуль,
в который входит данная стандартная процедура или функция, для чего имя
специализированного библиотечного модуля указывается в разделе uses. Затем в программе осуществляется вызов процедуры
или функции, для чего записывается ее имя и указываются фактические параметры,
например: Pi, Sin(x), Inc(x,5), Chr(125). Так
как после выполнения функции ее значение присваивается имени, то имя функции
используется в выражении.
Если в программе
возникает необходимость частого обращения к некоторой группе операторов, то
рационально сгруппировать такую группу операторов в самостоятельный блок, к которому
можно обращаться, указывая его имя. Такие разработанные программистом
самостоятельные программные блоки называются подпрограммами пользователя. Они являются основами модульного
программирования. Разбивая задачу на части и оформляя логически обособленные модули в виде процедур и
функций, программист реализует основные принципы широко используемого в
практике системного подхода и методов нисходящего проектирования.
При вызове
подпрограммы, определенной программистом, работа главной программы на некоторое
время приостанавливается и начинает выполняться вызванная подпрограмма. Она
обрабатывает данные, переданные ей из главной программы. По завершении
выполнения подпрограмма-функция возвращает главной программе результат
(подпрограмма-процедура не возвращает явно результирующего значения).
Передача данных из
главной программы в подпрограмму и возврат
результата выполнения функции осуществляется с помощью параметров. Параметром называется переменная, которой присваивается некоторое значение в рамках указанного
применения. Различают формальные параметры - параметры, определенные
в заголовке подпрограммы, и фактические параметры
- выражения, задающие конкретные значения при обращении к подпрограмме.
При обращении к подпрограмме ее формальные параметры замещаются
фактическими, переданными из главной программы.
Описание процедуры
состоит из заголовка процедуры и тела процедуры. Заголовок включает в себя
служебное слово procedure, имя процедуры и заключенные в круглые скобки список формальных параметров
с указанием их типов:
procedure <имя> (<список формальных параметров>);
Формальные параметры отделяются точкой с запятой (список однотипных
параметров может быть перечислен через запятую). После заголовка идут разделы описаний
(констант, типов, переменных, процедур и функций, используемых в процедуре) и
операторы языка ОР, реализующие алгоритм процедуры.
Например:
procedure f1 (x: real; var y:
real; var c: real); begin
y:=sin(x)/cos(x);
c:=ln(x)/ln(10);
end;
Формальные параметры нельзя описывать в разделе описаний процедуры.
Для обращения к
процедуре необходимо использовать оператор вызова процедуры. Он имеет следующий вид:
<имя процедуры>
(<список фактических параметров>);
Например:
f1(r, r1, r2);
Фактические параметры в списке отделяются друг от друга запятой.
Механизм применения формальных-фактических параметров обеспечивает замену первых параметров
последними, что позволяет выполнять процедуру с различными данными. Между
фактическими параметрами в операторе вызова процедуры и формальными параметрами
в заголовке процедуры устанавливается взаимно однозначное соответствие.
Замечание.
Количество, типы и порядок
следования формальных и фактических параметров должны совпадать.
Функция,
определенная пользователем, состоит из заголовка и тела функции. Заголовок
содержит зарезервированное слово function, идентификатор (имя) функции, заключенный в
круглые скобки, необязательный список формальных параметров и тип возвращаемого
функцией значения:
function <имя> (список формальных параметров): <тип
результата>;
Тело функции
представляет собой локальный блок, по структуре аналогичный программе.
Например:
function tan (c: real): real;
begin
tan:=sin(c)/ cos(c); end;
В теле функции
всегда должен быть один оператор,
присваивающий значение имени функции.
Обращение к функции
осуществляется по имени с указанием списка фактических параметров. Количество,
типы и порядок следования формальных и фактических параметров должны совпадать:
<имя функции> (<список фактических параметров>);
Например:
tg: =tan(x);
При использовании
процедур и функций переменные объявляются несколько раз в основной программе и подпрограммах.
Переменные и типы, определенные в основной программе до объявления
процедур и функций, называются глобальными – они доступны всем функциям и процедурам. Переменные, определенные
в какой-либо подпрограмме после раздела
описания процедур и функций, называются локальными.
Для правильного определения области действия идентификаторов
(переменных) необходимо придерживаться следующих правил:
-
каждая
переменная должна быть описана перед тем, как она будет использована;
-
областью
действия переменной является та подпрограмма, в которой она будет описана;
-
все переменные в
подпрограммах должны быть уникальными;
-
одна и
та же переменная может быть по-разному определена в каждой из подпрограмм;
-
если имя
подпрограммы совпадает с названием стандартной подпрограммы, то последняя
игнорируется, а выполняется подпрограмма пользователя;
-
если
внутри какой-либо процедуры встречается переменная с таким же именем, что и
глобальная переменная, то внутри процедуры будет действовать локальное описание;
-
каждая подпрограмма может
изменить значение глобальной переменной.
Рекурсия (рекурсивная процедура или функция) возникает, если функция или процедура вызывает
саму себя. Прямая рекурсия может
вызывать себя непосредственно, например:
function Factorial (n: LongInt) : LongInt; begin
Factorial:=n*Factorial(n-1);
end;
Рекурсивная процедура также может
вызывать себя косвенно, вызывая
вторую процедуру, которая, в свою очередь, вызывает первую:
procedure Ping(n: Integer);
begin
Pong(n-1);
end;
procedure Pong(n: Integer);
begin
Ping(n div 2);
end;
Классическим примером рекурсии является вычисление факториала.
Факториал числа n - это произведение целых чисел от 1 до n :
1× 2 × 3 ×..(n - 1)× n . Приведенное выражение можно переписать следующим
образом:
n!= n × ((n - 1)× (n - 2)×..× 3 × 2 ×1) = n × (n - 1)!
Рекурсивная функция вычисления факториала:
function Factorial (N: Integer):
Integer; begin
if (N<=0) then Factorial
:= 1
else
Factorial=N*Factorial(N-1);
end;
Функция сначала проверяет
число на условие
N £ 0. Для
чисел, меньших
нуля факториал не определен, но это
условие проверяется для подстраховки. Если бы функция проверила только условие
равенства числа нулю, то для отрицательных чисел рекурсия была бы бесконечной.
Если входное
значение меньше или равно нулю, функция возвращает значение, равное 1. Иначе
значение функции равно произведению входного значения на факториал, уменьшенный
на единицу.
Существуют два
фактора, которые гарантируют, что эта рекурсивная функция в конце концов
остановится. Во-первых, при каждом последующем вызове значение параметра N уменьшается на единицу.
Во-вторых, значение N ограничено нулем.
Когда значение достигает 0, функция заканчивает рекурсию.
Такое условие, как N £ 0 , которое останавливает рекурсию, называется
основным условием или условием остановки.
При каждом вызове
подпрограммы система сохраняет некоторые значения в стеке (стек –
упорядоченный список, в котором элементы добавляются и удаляются с
одного и того же конца списка). Если
рекурсивная процедура вызывается много раз, она может заполнить весь стек и вызвать ошибку переполнения стека.
Количество вызовов
рекурсивной функции зависит от объема памяти компьютера и количества данных,
которые программа помещает в стек.
4.2. Порядок
выполнения работы
Изучить операторы, используемые для организации
подпрограмм, выполнить контрольные примеры и задания соответствующего варианта.
5
Контрольный пример 4.1
Написать программу вычисления выражения
Z = A
+ A-3
![]() , в котором
, в котором
возведение в степень выполняется функцией
Step.
Решение.
1. Открыть новый проект Delphi: File
– New Application .
2 × AM
2.
Установить с
помощью Object Inspector следующие
свойства компонента
Form1:
Form1.Height = 345
Form1.Width = 396 Form1.BorderIcons
biMaximize = false
Form1.BorderStyle = bsSingle Form1.Position =
poScreenCenter
Form1.Caption = 'Контрольный пример 1'.
3. Расположить на форме следующие компоненты: три
компонента Edit, три компонента Label, один компонент Button. Установить
с помощью Object Inspector для них
следующие свойства:
Label1.Caption = 'A'
Label2.Caption = 'M' Label3.Caption = 'Z' Edit1.Text = '' Edit2.Text = ''
Edit3.Text = ''
Button1.Caption = 'Выполнить'.
4. Текст
программы приведен ниже:
unit Unit1; interface uses
Windows, Messages, SysUtils,
Variants, Classes, Graphics, Controls, Forms,
Dialogs, StdCtrls; type
TForm1 = class(TForm)
Label1: TLabel; Label2:
TLabel;
Label3: TLabel;
Edit1: TEdit;
Edit2: TEdit;
Edit3: TEdit;
Button1: TButton;
procedure
Button1Click(Sender: TObject); private
{ Private declarations }
public
{ Public declarations } end;
var
Form1: TForm1; M:integer;
A,Z,R:real;
implementation
{$R *.dfm}
// Функция вычисления
степени.
// N,Х – формальные параметры,
// результат, возвращаемый функцией в точку вызова
// имеет вещественный тип.
function Step(N:integer;
X:real):real; var i:integer; y:real;
begin y:=1;
for i:=1 to N do y:=y*x;
step:=y; // присваивание функции результата
// вычисления степени
end;
// Step
procedure TForm1.Button1Click(Sender: TObject);
begin
// ввод значения числа А и показателя степени М A:=StrToFloat(Edit1.Text); M:=StrToInt(Edit2.Text);
// Вызов функции с передачей ей фактических параметров
Z:=Step(5,A);
Z:= Z+Step(3,1/A);
if
M=0 then R:=1
else
if M>0 then R:=Step(M,A)
else R:=Step(-M,1/A);
Z:=Z/(2*R);
Edit3.Text:=FloatToStrF(Z,fffixed,7,5);
end;
end.
5.
Запустить программу на
компиляцию и выполнение.
Контрольный пример 4.2
Напишите процедуру,
которая по заданному интервалу и функции
определяет «ноль» функции с заданной точностью, используя метод деления
отрезка пополам. Известно,
что на границах
интервала функция принимает
значения, отличные по знаку. Определите «ноль» функции sin(x) = 0.2 × x
(наименьший положительный корень) на
произвольном интервале и b вводятся
с клавиатуры.
[a;b]. Числа a
Метод
деления отрезка пополам.
Пусть уравнение
F (x) = 0
имеет на
отрезке
[a, b]
единственный корень, причем
функция
F (x)
на этом отрезке
непрерывна. Разделим
отрезок [a, b]
пополам точкой
c = (a + b) . Если
![]() 2
2
F (c) ¹ 0 ,
то возможны два случая: либо
F (x)
меняет знак на отрезке
[a, c], либо на отрезке
[c, b]. Выбирая в каждом случае
тот из отрезков, на котором функция
меняет знак, и, продолжая
процесс деления отрезка пополам дальше, можно дойти до сколь угодно малого отрезка, содержащего корень уравнения. Если на каком-то этапе
процесса получен отрезок
[a , b ], содержащий корень, то, приняв приближенно
2![]()
x
= (a + b ) , получим ошибку, не превышающую значения
d = (b - a )
.![]()
2
Уточненный корень исходного уравнения:
Решение.
x =
x +
d .
1. Открыть новый проект Delphi: File – New Application.
2.
Установить с помощью Object Inspector следующие свойства формы:
Form1.Height = 392
Form1.Width = 289
Form1.BorderIcons biMaximize = false
Form1.BorderStyle = bsSingle
Form1.Position = poScreenCenter
Form1.Caption = 'Метод половинного
деления'
3.
Расположить
на форме следующие компоненты: три компонента Edit, три компонента Label, один компонент Button и один компонент BitBtn. Установить с помощью инспектора объектов
следующие свойства:
Label1.Caption
= 'a'
Label2.Caption
= 'b'
Label3.Caption
= 'решение' Edit1.Text = ''
Edit2.Text
= '' Edit3.Text = ''
Button1.Caption
= 'Счет' BitBtn1.Kind = 'bkClose'
BitBtn1. Caption = '&Закрыть'.
4. Для решения задачи запишем обработчик событий Button1.Click, щелкнув на компоненте Button1 (кнопка Счет) два раза левой кнопкой мыши. Текст соответствующей процедуры имеет вид:
procedure TForm1.Button1Click(Sender:
TObject); var a,b,x1,x2,y:real;
begin a:=StrToFloat(edit1.Text); b:=StrToFloat(edit2.Text); x1:=a;
x2:=b;
zero(x1,x2,y);
edit3.Text:=FloatToStrF(y,fffixed,8,4);
end;
Переменные, которые
необходимы для решения задачи, описаны в разделе глобальных переменных приложения.
Для реализации
метода половинного деления использовалась подпрограмма- процедура Zero,
которая должна располагаться в тексте модуля до того, как к ней происходит обращение:
procedure zero(a,b:real; var
res:real); const eps=1E-5;
var
s:boolean;x3:real;
function f(x:real):real;
begin
f:=sin(2*x)-0.2*x;
end;
// f
begin s:=f(a)< 0; repeat
x1:=(a+b)/2;
x3:=f(x1);
if
(x3<0)=s then a:=x1
else b:=x1; until
abs(a-b)<eps; res:=x1;
end; // zero
Раздел
констант приложения содержит величину допустимой погрешности вычислений EPS. В
процедуру Zero вложена функция
f,
которая задается
пользователем как левая часть уравнения f (x) = 0 . При обращении к
процедуре
Zero происходит отделение
корня: булева константа
S принимает значение
True, если
f (a) < 0
и False при
f (a) > 0 f. Операторы, стоящие между repeat
и until, повторяются до тех пор, пока выражение until не примет
значение True при проверке стоящего за ним условия, что означает
достижение нужной погрешности вычислений.
5. Запустить проект на компиляцию и выполнение.
Контрольный пример 4.3
Написать
рекурсивную функцию вычисления наибольшего
общего делителя
по алгоритму Эйлера:
Если B делится на A нацело,
то НОД (А, В) = А.
В
противном случае НОД(А, В) = НОД(B mod A, A).
Решение.
1. Открыть новый проект Delphi: File – New Application.
2. Установить с помощью Object Inspector следующие свойства формы:
Form1.Height = 347
Form1.Width = 359
Form1.BorderIcons biMaximize = false
Form1.BorderStyle = bsSingle
Form1.Position = poScreenCenter
Form1.Caption = 'Нахождение наибольшего общего
делителя'.
3. Расположить на форме следующие компоненты: три
компонента Edit, три компонента Label, один компонент Button и один компонент BitBtn. Установить
для них следующие свойства:
Label1.Caption
= 'a' Label2.Caption = 'b' Label3.Caption = 'НОД' Edit1.Text = '' Edit2.Text =
'' Edit3.Text = ''
Button1.Caption
= 'Вычислить НОД' BitBtn1.Kind = 'bkClose'
BitBtn1.
Caption = '&Закрыть'.
4. Текст
программы приведен ниже:
unit Unit1; interface uses
Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,
Dialogs, StdCtrls, Buttons;
type
TForm1 = class(TForm)
Button1: TButton; Edit1: TEdit; Edit2: TEdit; Label1: TLabel; Label2: TLabel;
BitBtn1: TBitBtn; Label3: TLabel; Edit3: TEdit;
procedure
Button1Click(Sender: TObject); private
{ Private declarations }
public
{ Public declarations } end;
var
Form1: TForm1; implementation
{$R *.dfm}
function NOD ( A, B :
LongInt) : LongInt; begin
if ( B mod A) = 0 then // если А делит В нацело, то значение
вычислено
NOD:=A
else // в противном случае функция вычисляется рекурсивно
NOD:=NOD(B
mod A, A);
end;
procedure
TForm1.Button1Click(Sender: TObject); var a,b:longint; f:longint;
begin
a:=StrToInt(edit1.Text);
b:=StrToInt(edit2.Text); f:=NOD(a,b);
Edit3.Text:=IntToStr(f);
end;
end.
5.
Запустить проект на
компиляцию и выполнение.
1. Что называется подпрограммой? В чем состоит
сходство и различие подпрограмм-процедур и подпрограмм-функций в языке Object Pascal?
2. В чем различие между стандартными и
определенными пользователем программами?
3. Опишите последовательность событий при вызове процедуры или функции.
4. Что называется параметром и каково его назначение? Что такое формальные и фактические параметры,
какова их взаимосвязь?
5. Каковы отличия параметров-переменных от параметров-значений,
особенности их описания и применения?
6. Чем различаются локальные и глобальные
параметры? Какова область их действия?
7.
Что такое рекурсия?
8.
Каковы особенности
параметров-процедур и параметров-функций?
4.4. Варианты заданий
Вариант 1
Задание
1. Написать программу для вычисления выражения
z(x) = (sign(x) + sign( y)) × sign(x + y) .
При решении задачи определите и используйте
функцию sign(знак числа): sign(x)=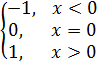
Задание 2. Написать процедуру вычисления определенного
интеграла
![]() методом прямоугольников:
методом прямоугольников: ![]() , где n – количество отрезков разбиения; y0,y1,…,yn – значения
фугкции на концах отрезков. Числа a и b – произвольные, вводятся с клавиатуры.
, где n – количество отрезков разбиения; y0,y1,…,yn – значения
фугкции на концах отрезков. Числа a и b – произвольные, вводятся с клавиатуры.
Задание 3*. Напишите рекурсивную функцию вычисления i-го число Фибоначчи. Вычислите f (k ), k = 15, 20, 30,
40. Функция f (n) определена для целых чисел следующим образом:
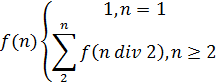
Вариант 2
Задание 1. Написать программу вычисления выражения
![]() где
где ![]()
вычисление величин ![]() и max(a,b) оформить в виде подпрограммы- функции. Числа s и t вводятся
с клавиатуры.
и max(a,b) оформить в виде подпрограммы- функции. Числа s и t вводятся
с клавиатуры.
Задание 2. Написать процедуру вычисления
определенного интеграла
![]() методом трапеций:
методом трапеций: ![]() , где n – колтчество отрезков разбиения; y0,y1,…,yn – значения функции на концах отрезков. Числа a и b – произвольные, вводятся с клавиатуры.
, где n – колтчество отрезков разбиения; y0,y1,…,yn – значения функции на концах отрезков. Числа a и b – произвольные, вводятся с клавиатуры.
Задание 3*. Создайте программу вычисления числа сочетаний из N по M .
Число сочетаний определяется по формуле
M = N! .
Для вычисления
C![]()
N M!×(N - M )!
факториала напишите рекурсивную функцию.
Вариант 3
Задание 1. Написать программу вычисления выражения
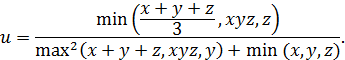
Нахождение
максимального и минимального значения из
трех чисел оформить
в виде подпрограмм-функций max(a, b, c) и min(a, b, c).
Задание 2. Написать процедуру вычисления
определенного интеграла
![]() методом прямоугольников:
методом прямоугольников: ![]() , где n – количество отрезков разбиения; y0,y1,…,yn – значения
фугкции на концах отрезков. Числа a и b – произвольные, вводятся с клавиатуры.
, где n – количество отрезков разбиения; y0,y1,…,yn – значения
фугкции на концах отрезков. Числа a и b – произвольные, вводятся с клавиатуры.
Задание 3*. Написать рекурсивную функцию, которая по заданному вещественному n вычисляет величину xn согласно формуле
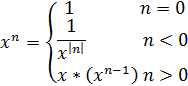
Вариант 4
Задание 1. Даны координаты вершин многоугольника (x1, y1 ); (x2 , y2 );…(x5 , y5 ). Найти его периметр. Вычисление
расстояния между вершинами оформить в виде подпрограммы-функции.
Задание 2. Написать процедуру вычисления определенного интеграла
![]() по
формулеСимпсона
по
формулеСимпсона![]() , где 2*n –
количество отрезков разбиения; y0 , y1,…, y2n – значения
функции на концах отрезков. Числа a и b – произвольные, вводятся с клавиатуры.
, где 2*n –
количество отрезков разбиения; y0 , y1,…, y2n – значения
функции на концах отрезков. Числа a и b – произвольные, вводятся с клавиатуры.
Задание 3*. Написать
рекурсивную функцию, которая вычисляет![]() по следующей
формуле:
по следующей
формуле: ![]()
За ответ
принять приближение, для которого выполняется условие | yn - yn+1| < 0.0001.
Вариант 5
Задание 1. Даны действительные числа s, t. Написать программу вычисления выражения
f (t, - 2s,1,17)+ f (2, 2,t, s - t) . Вычисление функции
![]()
Оформить
в виде подпрограммы-функции
Задание 2. Написать процедуру вычисления
определенного интеграла
![]() методом прямоугольников:
методом прямоугольников: ![]() , где n – количество отрезков разбиения; y0,y1,…,yn – значения
фугкции на концах отрезков. Числа a и b – произвольные, вводятся с клавиатуры.
, где n – количество отрезков разбиения; y0,y1,…,yn – значения
фугкции на концах отрезков. Числа a и b – произвольные, вводятся с клавиатуры.
Задание 3*. Задано
вещественное число a > 0 . Вычислить ![]()
Вычисление корней
![]() оформить в
виде подпрограммы. Корни вычислять с
точностью E = 0.00001 по итерационной формуле:
оформить в
виде подпрограммы. Корни вычислять с
точностью E = 0.00001 по итерационной формуле:
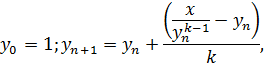
приняв за ответ
приближение, для котрого |yn+1-yn|<E. Вычисление yk оформить в виде рекурсивной
подпрогаммы.
Вариант 6
Задание 1.
Для двух квадратных уравнений a1 x 2 + b1 x + c1 = 0 и
a2 x 2 + b2 x + c2 = 0 определить, имеют
ли они общие
корни. Вывести на экран
корни уравнения, которые
не совпадают. Решение
уравнений оформить в виде
подпрограммы-функции. Числа a1, b1, c1, a2, b2 , c2 вводятся с клавиатуры.
Задание 2. Написать процедуру вычисления
определенного интеграла
![]() по формулеСимпсона
по формулеСимпсона![]() , где 2*n – количество отрезков
разбиения; y0 , y1,…, y2n – значения функции на концах отрезков. Числа a и b – произвольные, вводятся с клавиатуры.
, где 2*n – количество отрезков
разбиения; y0 , y1,…, y2n – значения функции на концах отрезков. Числа a и b – произвольные, вводятся с клавиатуры.
Задание 3*. Написать
процедуру сложения двух дробей, результатом которого является несократимая
правильная дробь. Использовать рекурсивную программу нахождения НОД
Вариант 7
Задание 1. Написать программу вычисления выражения
![]() , Вычисление
, Вычисление ![]() ;
; ![]() и
и ![]() оформить в виде подпрограммы-функции.
оформить в виде подпрограммы-функции.
Задание 2. Написать процедуру вычисления определенного интеграла
![]() методом прямоугольников:
методом прямоугольников: ![]() , где n – количество отрезков разбиения; y0,y1,…,yn – значения
фугкции на концах отрезков. Числа a и b – произвольные, вводятся с клавиатуры.
, где n – количество отрезков разбиения; y0,y1,…,yn – значения
фугкции на концах отрезков. Числа a и b – произвольные, вводятся с клавиатуры.
Задание 3*. Написать программу вычисления выражения
![]() в виправильной дроби, где A, B, C, E, F– целые
числа. Сложение двух дробей
оформить как подпрограмму-функцию. Использовать рекурсивную программу
нахождения НОД.
в виправильной дроби, где A, B, C, E, F– целые
числа. Сложение двух дробей
оформить как подпрограмму-функцию. Использовать рекурсивную программу
нахождения НОД.