Растровое преобразование графических примитивов

• Алгоритмы Брезенхема растровой дискретизации отрезка

• Алгоритмы Брезенхема растровой дискретизации окружности

• Алгоритмы Брезенхема растровой дискретизации эллипса

Экран растрового дисплея можно рассматривать как матрицу дискретных элементов, или пикселей. Процесс определения пикселей, наилучшим образом аппроксимирующих некоторую геометрическую фигуру, называется разложением в растр, или построением растрового образа фигуры. Построчная визуализация растрового образа называется растровой разверткой данной фигуры.

В компьютерной графике необходимо иметь возможность генерировать отрезки, многоугольники и многогранники (представляющиеся как совокупности определенным образом ориентированных отрезков), окружности, эллипсы, параболы, гиперболы и т.д. Алгоритмы генерации таких фигур основаны на схожих принципах. Так, разложение фигур в растр базируется в большинстве случаев на пошаговом методе. Он предполагает построение фигуры или ее части путем поочередного перехода от текущего пикселя к одному из соседних пикселей, который, в свою очередь, становится текущим. При этом на каждом шаге вопрос о выборе конкретного перехода среди альтернативных вариантов решается с использованием, по сути дела, аналогичных с геометрической точки зрения критериев.

Алгоритмы Брезенхема растровой дискретизации отрезка

При построении растрового образа отрезка необходимо:

• Установить критерии "хорошей" аппроксимации (отрезок должен начинаться и кончаться в заданных точках и при этом выглядеть сплошным и прямым);

• Кроме того, яркость вдоль отрезка должна быть одинаковой и не зависеть от наклона отрезка и его длины (горизонтальные и вертикальные отрезки всегда будут ярче наклонных, а постоянная яркость вдоль отрезка опять же достигается на вертикальных, горизонтальных и наклоненных под углом в 45° линиях);

• Алгоритм должен работать быстро. Для этого необходимо по возможности исключить операции с вещественными числами;

Более приемлемым для генерации отрезков считается алгоритм Брезенхема. В соответствии с ним отрезок вычерчивается пошагово от начала - точки P₁ с координатами (x₁,y₁) - до конца - точки P₂ с координатами (x₂ ,y₂). Важную роль при этом имеет ориентация отрезка. Ее определяет положение точки P₂ относительно начала координат, которое условно совмещается с точкой P₁ (рис.6.1).

При попадании точки P₂ в какой-либо октант координатной плоскости говорят о том, что весь отрезок расположен в этом октанте (так, например, считается, что отрезок P₁P₂ на (рис.6.1) расположен в седьмом октанте). На каждом шаге в зависимости от величины тангенса угла наклона отрезка (назовем его угловым коэффициентов и обозначим как m) единичное приращение одной из координат задается безусловно. Необходимость единичного изменения другой координаты определяется по знаку рассчитываемой на каждом шаге величины e (ошибки), которая оценивает расстояние между действительным положением отрезка и ближайшими по данной координате адресуемыми точками растра. Если модуль углового коэффициента не больше единицы (1, 4, 5 и 8 октанты), на каждом шаге x изменяется на единицу, а y либо не изменяется, либо изменяется на единицу (рис.6.1), в зависимости от знака ошибки. При модуле углового коэффициента больше единицы (2, 3, 6 и 7 октанты), наоборот, y безусловно изменяется на единицу, а знак ошибки используется для принятия решения об изменении величины x. Знак же приращений координат x и y зависит от конкретной ориентации отрезка (так, при генерации отрезка P₁P₂ , изображенного на рис.6.1, на каждом шаге y безусловно будет получать приращение -1, а x - либо изменяться на +1, либо оставаться неизменным).

Ознакомимся более подробно с принципами работы вещественного алгоритма Брезенхема для генерации отрезка в первом октанте (впоследствии он будет преобразован в целочисленный и обобщен на случай произвольной ориентации отрезка). Значение углового коэффициента отрезка, расположенного в первом октанте, лежит в диапазоне 0 <= m <= 1, и на каждом шаге x безусловно получает приращение +1, а вопрос о приращении y на +1 решается с учетом знака ошибки е. Каким образом она формируется и используется для выбора решения, можно рассмотреть на следующем примере.

Допустим, необходимо построить отрезок в первом октанте с угловым коэффициентом m = 3/8. Точка начала отрезка с координатами (x₁ , y₁) (впрочем, как и точка его конца) совпадает с каким- либо узлом растра. Активизируем пиксель с такими же координатами адресуемой точки и инициализируем начальное значение ошибки е = -1/2 (рис. 6.2). Горизонтальная координата следующей адресуемой точки очевидна: x = x₁ +1.

Новое значение ошибки рассчитывается путем добавления к ней значения углового коэффициента: е = е+m = -1/2+3/8 = -1/8. Отрицательное значение ошибки свидетельствует о том, что пересечение реального отрезка с прямой x = x₁ +1 расположено ближе к прямой y = y₁, чем к прямой y = y₁ +1 (рис.6.2), поэтому точка растра (x₁ + 1, y₁) лучше аппроксимирует ход отрезка, чем точка (x₁ + 1,y₁ +1). Активизировав пиксель с координатами адресуемой точки (x₁ + 1,y₁), делаем следующий шаг: x = x₁ + 2, e=e+m=-1/8+3/8=1/4; т.к. ошибка положительна, задаем единичное приращение по вертикали y = y₁ +1. Активизируем пиксель с адресуемой точкой (x₁ + 2, y₁ +1). Вместе с тем, как только ошибка стала положительной, ее значение необходимо скорректировать путем вычитания единицы: e = е -1 = 1/4 -1 = - 3/4. Дальнейшие действия алгоритма аналогичны: x = x₁ + 3, e = - 3/4 + 3/8 = - 3/8, y не увеличивается, активизируется пиксель (x₁ + 3,y₁ +1) и т.д. Отметим здесь только еще один нюанс: если на каком-либо шаге ошибка принимает нулевое значение, нет предпочтительного варианта задания вертикальной координаты (т.к. отрезок пересекает соответствующую вертикаль строго посередине между двумя узлами растра); для определенности алгоритм Брезенхема в этом случае дает приращение y на единицу и корректирует значение ошибки. Поэтому при расчете следующей точки в рассмотренном только что примере результаты будут такими: x = x₁ + 4, e = -3/8+3/8 = 0, y = y₁ + 2, активизация пикселя с координатами адресуемой точки (x₁ + 4, y₁ + 2 ), корректировка значения ошибки e = 0 -1 = -1 (см. рис.6.2).

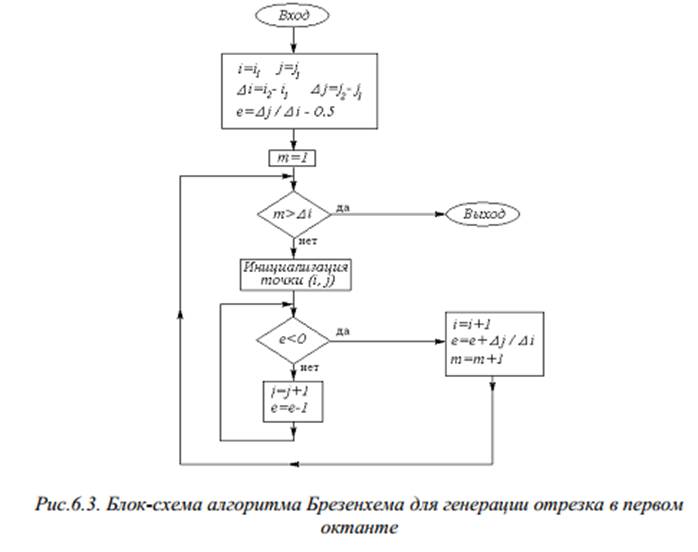
Алгоритм Брезенхема (и его программная реализация) для генерации отрезка в первом октанте на блок-схеме выглядит так:

Program Lr_3; { Алгоритмы Брезенхема растровой дискретизации отрезка }

Uses GraphABC, CRT;

Const i1=100; i2=300; j1=100; j2=300;

Var i,j,di,dj,m:integer; e:real;

Begin

i:=i1; j:=j1;

di:=i2-i1; dj:=j2-j1;

e:=dj/di-0.5; m:=1;

While m<=di do begin

Delay(10);

PutPixel(i,j,clBlack);

While e>0 do begin

j:=j+1;

e:=e-1;

end;

i:=i+1;

e:=e+dj/di;

m:=m+1;

end;

end.

Алгоритм Брезенхема для генерации окружности

Существуют несколько версий алгоритма Брезенхема для генерации окружности. Они имеют ряд общих признаков. Так, во всех этих версиях изначально пошагово генерируется одна восьмая часть окружности, расположенная во втором октанте координатной плоскости, при условии, что центр окружности совмещен с точкой начала координат (рис. 6.4); причем ее построение начинается в точке ( x = 0, y = R) и осуществляется в направлении по часовой стрелке.

При этом y является монотонно убывающей функцией x. Остальные части окружности достраиваются последовательными симметричными отражениями: сгенерированной восьмой части во втором октанте - относительно прямой y = x в первый октант, а полученной после этого четверти окружности в первом квадранте - относительно координатных осей x и y, а также точки начала координат в четвертый, второй и третий квадранты соответственно. Во всех случаях арифметика целочислена, при анализе альтернативных вариантов перехода (от пикселя к пикселю) используются не численные значения, а только знаки определенных величин (критериев), что упрощает и ускоряет вычисления. Отличаются версии, по сути дела, только несколько разными с математической, в том числе геометрической точки зрения подходами. Рассмотрим кратко первую, самую раннюю, версию алгоритма (сейчас она практически вышла из употребления) и одну из тех, которые появились позже и применяются в настоящее время.

Теоретические положения, на которых базируется первая версия алгоритма Брезенхема, пригодны для построения четверти (а не одной восьмой части) окружности в первом квадранте. При нахождении в этом квадранте в некоторой текущей точке растра с координатами (x_i,y_i) есть только три варианта выбора очередного пикселя (рис.6.5): по горизонтали вправо (направление H), по диагонали вниз и вправо (направление D) и по вертикали вниз (направление V). Вместе с тем, в каждой такай ситуации возможны пять типов пересечений реальной окружности и сетки растра (рис. 6.5).

В качестве первого критерия для выбора очередного шага используется разность между квадратами расстояний от центра окружности до диагональной (по отношению к текущей) точки, т.е. точки с координатами (x_i + 1,y_i -1), и до реальной окружности: ∆_i = (x_i + 1)²+(y_i -1)²- R².

При ∆_i < 0 диагональная точка находится внутри окружности, т.е. это случаи пересечения 1 или 2. Ясно, что в данной ситуации следует выбрать либо точку (x_i +1, y_i), т.е. шаг H, либо точку (x_i + 1,y_i -1), т.е. шаг D.

Вторым критерием перехода при таких условиях служит величина: δ=((x_i +1)²+ y_i²- R²) – ((x_i +1)²+ (y_i -1)²- R²)

Она представляет собой разность двух модулей: под первым из них стоит разность между квадратами расстояний от центра окружности до горизонтальной (по отношению к текущей) точки и до реальной окружности; под вторым - разность между квадратами расстояний от центра окружности до диагональной (по отношению к текущей) точки и до реальной окружности.

При δ < =0 расстояние от окружности до горизонтальной точки не больше расстояния до диагональной точки, и следует выбирать горизонтальную точку, т.е. шаг H.

При δ > 0 выбирается диагональная точка, т.е. шаг D, т.к. расстояние от окружности до нее меньше. Вместе с тем, при варианте пересечения 1 (см. рис.6.5)

(x_i +1)²+ y_i²- R²>= 0, (x_i +1)²+ (y_i -1)²- R²< 0, т.к. горизонтальная точка лежит вне или на окружности, а диагональная - внутри нее, поэтому δ можно вычислить по формуле:

δ = (x_i +1)²+ y_i- R²+ (x_i +1)²+ (y_i -1)²- R²; или (после преобразования с учётом выражения для ∆i: δ = 2 (∆_i + y_i )-1.

При варианте пересечения 2 (см. рис.6.5) расстояние от окружности до горизонтальной точки безусловно меньше расстояния от нее же до диагональной точки, и выбирать следует горизонтальную. При этом обе точки лежат внутри окружности, поэтому: (x_i +1)²+ y_i²- R²<0, (x_i +1)²+ (y_i -1)²- R²< 0, и для расчета δ можно использовать ту же формулу, что и при варианте 1, т.к. она дает заведомо отрицательное значение.

Если ∆i > 0, то диагональная точка находится вне окружности, т.е. это случаи пересечения 3 или 4

(рис.6.5). Выбирать следует либо точку ( x_i +1, y_i -1), т.е. шаг D, либо точку (x_i,y_i -1), т.е. шаг V.

Можно показать (аналогично тому, как это было сделано для предыдущего случая), что критерием для выбора при этом является величина δ = 2 (∆_i - x_i )-1.

при δ < =0 выбирается диагональная точка, т.к. расстояние от окружности до нее не больше, чем до вертикальной (по отношению к текущей);

при δ >0 выбирается вертикальная точка, т.к. расстояние от окружности до нее меньше, чем до диагональной.

Очевидно, что при ∆i = 0 диагональная точка ( x_i + 1,y_i -1) расположена непосредственно на окружности (вариант пересечения 5 на рис.6.5), и выбирается именно она.

Подведем итог. Согласно рассматриваемой версии алгоритма Брезенхема:

Если сгенерирована четверть окружности в первом квадранте, для построения полной окружности эту четверть следует симметрично отразить относительно осей x и y и точки начала координат, т.е. активизировать не только выбранные пиксели (x_i,y_i), но и симметричные им пиксели (x_i - y_i) (- xi>yi) и (- xi>- yi).

Ниже представлена блок-схема составленная с учетом изложенных соображений алгоритма для прорисовки окружности с исходной генерацией ее четверти:

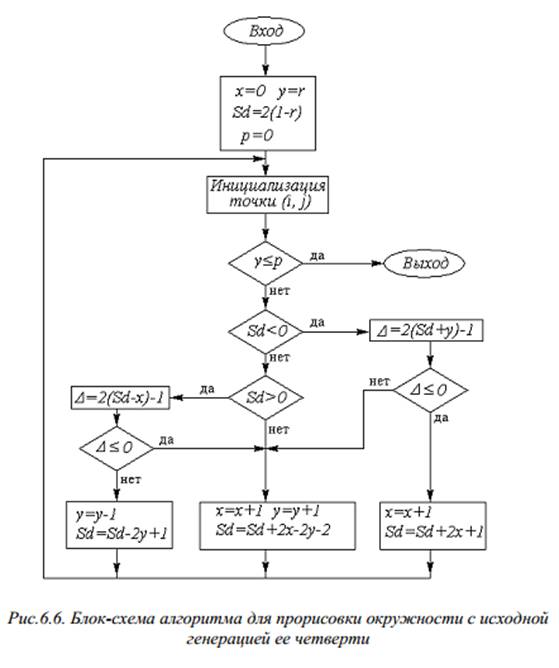
Реализация действия Алгоритма Брезенхема для генерации окружности

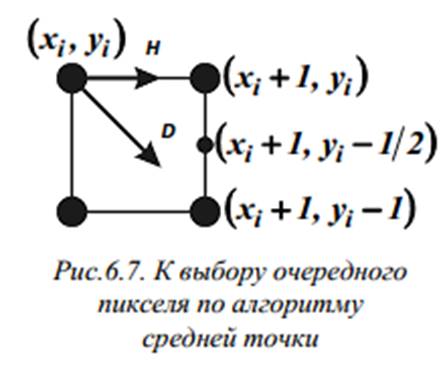
Рассмотрим теперь более позднюю и достаточно простую версию алгоритма Брезенхема (алгоритм средней точки). В ней учитывается то обстоятельство, что при построении одной восьмой части окружности во втором октанте на каждом шаге возможны только два варианта перехода: по горизонтали, т.е. шаг H, и по диагонали, т.е. шаг D (рис.6.7).

Выбор между ними осуществляется с использованием единственного критерия - разности между квадратами расстояний от центра окружности до точки с координатами (x_i +1, y_i -1/2) (так называемой средней точки, расположенной как раз посередине между альтернативными точками перехода, см. рис.6.7) и до реальной окружности: ∆_i = (x_i + 1)²+(y_i -1/2)²- R².

Если ∆ i < 0, средняя точка находится внутри окружности, и выбирается шаг H; если ∆_i > 0, эта точка расположена вне окружности или непосредственно на ней, и выбирается шаг D. При переходе к очередному текущему пикселю можно использовать следующие выражения (для ∆_i+1 - без вывода):

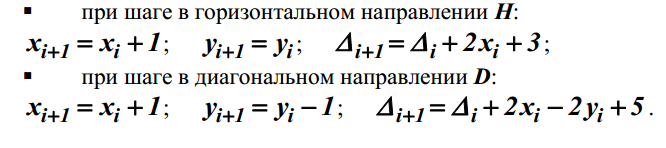
Алгоритмы Брезенхема растровой дискретизации эллипса

Существуют несколько версий алгоритма генерации эллипса. Все они являются, по сути дела, обобщениями соответствующих версий алгоритма Брезенхема для генерации окружности. Основные принципы построения эллипса схожи во всех версиях.

Центр эллипса условно совмещается с точкой начала координат (как и при построении окружности), а оси эллипса - с координатными осями. При этом

уравнение эллипса имеет вид

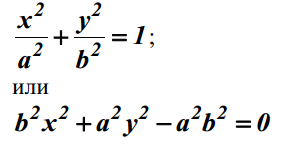
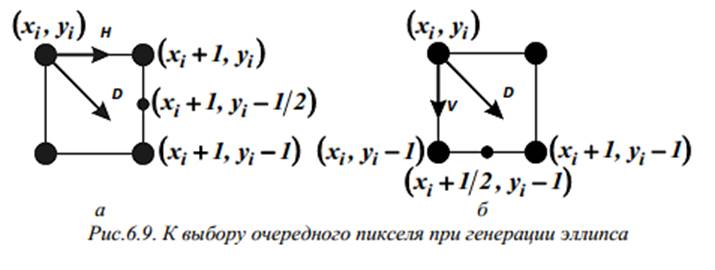
Генерируется одна четвертая часть эллипса в первом квадранте; затем эта четверть симметрично отражается во второй, третий и четвертый квадранты (рис.6.8). Пошаговое построение четверти эллипса начинается в точке (x = 0,y = b) и осуществляется в направлении по часовой стрелке. Данный процесс реализуется в два этапа: на первом прорисовывается участок, на котором модуль углового коэффициента принимает значения в диапазоне от нуля до единицы (на рис.6.8 - участок 1); на втором - участок, на котором угловой коэффициент по модулю больше единицы (на рис.6.8 - участок 2). При решении вопроса о том, на каком шаге следует перейти от построения первого участка к построению второго участка, можно использовать следующие соображения. Теоретически для первого участка справедливо неравенство b²x < a²y, для второго - неравенство b²x > a²y; в точке же, разделяющей эти участки, выполняется условие b²x = a²y. Подстановка этого условия в уравнение эллипса и решение последнего в общем виде относительно x дает выражение для расчета горизонтальной координаты в точке, разделяющей участки:

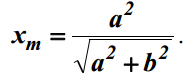
При нахождении в некоторой текущей точке с координатами (x_i,y_i) на первом участке есть только два варианта перехода к очередной точке (как и при построении одной восьмой части окружности во втором октанте): по горизонтали, т.е. шаг H, и по диагонали, т.е. шаг D (рис.6.9а). Критерий перехода формируется путем подстановки в левую часть уравнения эллипса (второго из двух, приведенных выше) координат точки (x, + 1,y, -1/2 ) (т.е. средней точки, расположенной посередине между альтернативными точками перехода):

∆_i = b²(x_i +1)²+ a²(y_i -1/2)²- a²b²; с геометрической точки зрения получаемая величина пропорциональна разности квадратов вертикальных координат средней точки и точки, принадлежащей четверти эллипса, при x = x, +1 (коэффициентом пропорциональности служит a² ).

Если ∆_i < 0, эллипс проходит выше средней точки, и выбирается шаг H; если ∆_i<= 0, эллипс проходит ниже этой точки или непосредственно через нее, и выбирается шаг D.

При переходе к очередному текущему пикселю можно использовать следующие выражения (для ∆_ii+1 - без вывода):

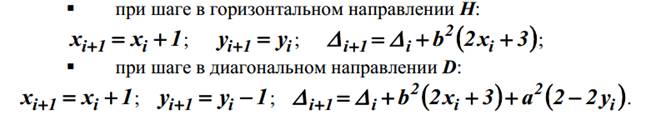
При нахождении текущей точке (x_i,y_i) на втором участке вариантов перехода к очередной точке тоже два: по диагонали, т.е. шаг D, или по вертикали, т.е. шаг V (рис.6.9б). Критерий перехода формируется по аналогии с предыдущим, но в данном случае используется средняя точка ( x_i +1/2 ,y_i -1):

∆_i = b²(x_i +1/2)²+ a²(y_i -1)²- a²b²;

получаемая величина пропорциональна разности квадратов горизонтальных координат средней точки и точки, принадлежащей четверти эллипса, при y = y_i -1 (коэффициент пропорциональности здесь равен b²).

Если ∆_i < 0, эллипс проходит правее средней точки, и выбирается шаг D; если ∆_i >= 0, эллипс проходит левее этой точки или непосредственно через нее, и выбирается шаг V.

Переход к очередному текущему пикселю осуществляется с использованием следующих выражений (для ∆_{i +1} - без вывода):

Вопрос о выборе критерия, на основании которого осуществляется переход от построения первого участка к построению второго участка, решается неоднозначно. Будем считать, что первый участок следует выстраивать до тех пор, пока горизонтальная координата точки, сдвинутой вправо на 1/2 относительно текущей, меньше чем x_m, т.е.

пока выполняется условие x_i +1/2 < x_m или (что то же самое) x_i < x_m -1/2 = x_m'.

Реализация действия Алгоритма Брезенхема для генерации эллипса