Лекция 3.
Способы задания движения. Переход от
уравнения движения в декартовых координатах к естественному уравнению движения.
Движение точки по
отношению к выбранной системе отсчета считается заданным ,
если известен способ , при помощи которого можно определить положение точки в
любой момент времени.
Следовательно , задать движение точки значит
это значит указать способ , позволяющий в любой момент времени определить её
положение по отношению к выбранной системе отсчета.
1.Векторный
способ.
Положение
точки в пространстве будет вполне определенно , если её радиус-вектор ![]() , проводимый из какого-либо заданного центра ,
известен как функция времени, т.е.
, проводимый из какого-либо заданного центра ,
известен как функция времени, т.е. ![]() =
=![]() Следует иметь иметь в виду , что задать вектор
, как функцию времени , значит уметь находить её модуль и направление в любой
момент времени.
Годографом какого-либо вектора называют кривую
, которую вычерчивает конец этого вектора при изменении его
аргумента.
Например: Годографом радиус-вектора определяющего положение точки , будет траектория точки.
Следует иметь иметь в виду , что задать вектор
, как функцию времени , значит уметь находить её модуль и направление в любой
момент времени.
Годографом какого-либо вектора называют кривую
, которую вычерчивает конец этого вектора при изменении его
аргумента.
Например: Годографом радиус-вектора определяющего положение точки , будет траектория точки.
2.Координатный
способ.
Способ
задания движения , заключающийся в задании координат
точки как известных функций времени , называется координатным способом
задания движения и требует выбора конкретной системы координат. При рассмотрении
движения в прямоугольной декартовой системе координат указанный способ заключается
в задании координат ![]() точки
точки ![]() как известных функций времени.
как известных функций времени.
![]() ,
, ![]()
![]() Во многих
случаях бывает предпочтительнее использовать цилиндрические или сферические
координаты
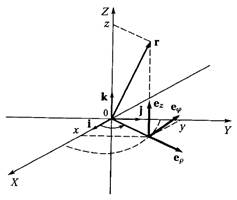
В цилиндрических координатах (рис. 1) положение точки определяется
радиусом
Во многих
случаях бывает предпочтительнее использовать цилиндрические или сферические
координаты
В цилиндрических координатах (рис. 1) положение точки определяется
радиусом ![]() углом
углом ![]() (азимутом) и аппликатой
(азимутом) и аппликатой ![]() .
Движение будет задано , если
.
Движение будет задано , если ![]() будут известными функциями времени
будут известными функциями времени ![]()
![]()
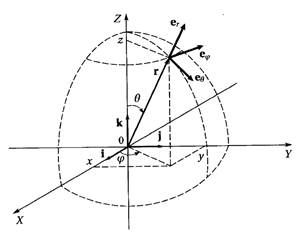
В сферических координатах (рис.2) положение точки
определяется полярным радиусом ![]() углом
углом ![]() и углом
и углом ![]() .
Движение будет задано , если
.
Движение будет задано , если ![]()
![]()
![]() известные
функции времени.
известные
функции времени.
Формулы , связывающие
цилиндрические и сферические координаты с декартовыми , соответственно
будут ![]() ,
, ![]()
![]()
![]() ,
, ![]() При движении точки в
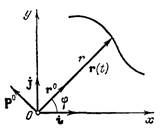
плоскости иногда целесообразно использовать полярные координаты. В этом
случае нужно задать в виде функций времени координаты
При движении точки в
плоскости иногда целесообразно использовать полярные координаты. В этом
случае нужно задать в виде функций времени координаты ![]() (рис. 3)
(рис. 3)
![]()
Уравнение (1) движения точки представляют
одновременно и уравнением траектории в параметрической форме
, где параметром является время t. Если требуется определить
уравнение траектории в координатной форме , то нужно
исключить из этих уравнений время t.
3.Естественный
способ.
При
естественном способе задания движения указываются траектория точки и закон её
движения по этой траектории.
Пусть точка движется по отношению к выбранной
системе отсчета по заданной траектории , определяемый
уравнениями: ![]()
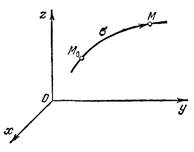
Пусть ![]() какая-либо фиксированная точка на траектории , мы определим положение точки
какая-либо фиксированная точка на траектории , мы определим положение точки ![]() в любой момент времени , если будем знать ,
как изменяется дуга
в любой момент времени , если будем знать ,
как изменяется дуга ![]() (см. рис. 4) со временем
(см. рис. 4) со временем ![]() Эта зависимость называется законом движения.
Кривая , построенная на плоскости
Эта зависимость называется законом движения.
Кривая , построенная на плоскости ![]() выражающая зависимость
выражающая зависимость ![]() называется
графиком движения.
Если движение происходит в
сторону возрастания дуги
называется
графиком движения.
Если движение происходит в
сторону возрастания дуги ![]() , то дифференциал
дуги
, то дифференциал
дуги
![]() будет
положительным , если движение происходит в сторону убывания дуги, то
дифференциал дуги будет отрицательным. Отметим , что
путь
будет
положительным , если движение происходит в сторону убывания дуги, то
дифференциал дуги будет отрицательным. Отметим , что
путь ![]() проходимый точкой всегда будет возрастать и ,
следовательно , положителен , т.е.
проходимый точкой всегда будет возрастать и ,
следовательно , положителен , т.е. ![]() .
Все рассмотренные способы задания движения взаимосвязаны. Пусть движение
задано координатным способом в виде (1). Очевидно , что при этом проекция радиуса-вектора
.
Все рассмотренные способы задания движения взаимосвязаны. Пусть движение
задано координатным способом в виде (1). Очевидно , что при этом проекция радиуса-вектора ![]() (рис. 5) на оси координат равны координатам
точки
(рис. 5) на оси координат равны координатам
точки ![]() и , можно записать
и , можно записать
![]() где
где ![]()
![]()
![]() единичные векторы осей
единичные векторы осей ![]()
![]() .
.
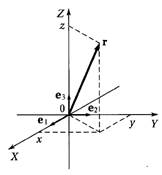
Модуль ![]() найдется по формуле
найдется по формуле ![]() а направление
определяется направляющими косинусами
а направление
определяется направляющими косинусами ![]() Рассмотрим переход от
координатного способа к естественному. Пусть движение
задано уравнением (1). Исключая из этих уравнений время
Рассмотрим переход от
координатного способа к естественному. Пусть движение
задано уравнением (1). Исключая из этих уравнений время ![]() , получим уравнение
траектории (4).
, получим уравнение
траектории (4).
Найдем теперь закон движения ![]() .
.
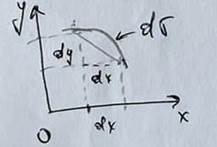
Дифференциал
дуги может быть найден по формуле ![]()
где ![]()
![]()
![]() дифференциалы
координатной точки
дифференциалы
координатной точки ![]()
![]() ,
, ![]()
Формулу для ![]() можно переписать в виде
можно переписать в виде
![]()
Интегрируя в промежутке от 0 до![]() получим закон
движения
получим закон
движения
![]()