Лекция 8. Векторное произведение векторов.

Опр. Векторным произведением вектора   на вектор   называется вектор , обозначаемый символом   и удовлетворяющий следующим условиям:

1) длина вектора    равна произведению длин векторов   и   на синус угла   между ними, то есть

;

2) вектор    ортогонален каждому из векторов   и  ;

3) вектор   направлен так, что тройка векторов   является правой.

Пример. Найти длину векторного произведения векторов  и  , если ; ; .

Решение. .

Пример. Найти векторное произведение векторов  и  , если ; , а скалярное произведение .

Решение. Из школьного курса математики мы знаем, что

.

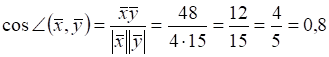Тогда .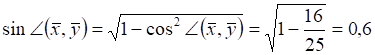

И векторное произведение вычислим по формуле:

.

Теорема 1. Необходимым и достаточным условием коллинеарности двух векторов является равенство нулю векторного произведения этих векторов.

Теорема 2. Длина (или модуль) векторного произведения векторов 

равна площади S параллелограмма, построенного на приведённых к общему началу векторах   и  .

Следствие. Площадь треугольника, построенного на приведённых к общему началу векторах    и  равна половине длины векторного произведения этих векторов.

Алгебраические свойства:

1. (свойство антиперестановочности сомножителей);

2. (сочетательное относительно числового множителя

свойство);

3. (распределительное относительно суммы векторов свойство);

4. для любого вектора .

Выражение векторного произведения в декартовых координатах:

Теорема. Если два вектора и   определены своими декартовыми прямоугольными координатами и , то векторное произведение  этих векторов имеет вид

.

Пример. Даны векторы , .

Найти:

1) Координаты векторного произведения этих векторов;

2) Длину векторного произведения этих векторов.

Решение.

1)

= .

2) .

Опр. Пусть даны три произвольных вектора  ,   и  . Если вектор   векторно умножается на вектор  , а затем получившийся при этом вектор  скалярно умножается на вектор  , то в результате получается число , называемое смешанным произведением векторов ,   и  .

Геометрический смысл смешанного произведения:

Теорема. Смешанное произведение   равно объёму параллелепипеда, построенного на приведённых к общему началу векторах  ,   и  , взятому со знаком плюс, если тройка   правая, и со знаком минус, если тройка   левая. Если же векторы ,  и   компланарны, то   равно нулю.

Следствие 1. Справедливо равенство  .

Следствие 2. Необходимым и достаточным условием компланарности трёх векторов является равенство нулю их смешанного произведения.

Следствие 3. Смешанное произведение трёх векторов, два из которых совпадают, равно нулю.

Выражение смешанного произведения в декартовых координатах:

Теорема. Если три вектора ,   и   определены своими декартовыми прямоугольными координатами , и , то смешанное произведение  равно определителю, строки которого соответственно равны координатам перемножаемых векторов, т.е.

.

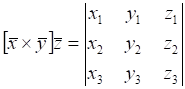Следствие. Необходимым и достаточным условием компланарности трёх векторов  , и , является равенство нулю определителя, строками которого служат координаты этих векторов, т.е. равенство

.

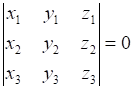Пример. Даны векторы , и . Найти:

3) смешанное произведение векторов;

4) объем параллелепипеда, построенного на этих векторах.

Решение.

1) ;

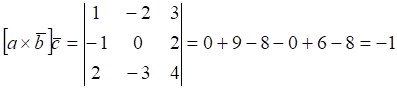2) .