Оглавление

9. Теорема А.Г. Витушкина об оценке энтропии аналитических функций

Пусть, как и выше, – область комплексной плоскости, ограниченная эллипсом с фокусами и 1 и суммой полуосей , и пусть при и класс состоит из всех вещественных аналитических на отрезке функций , для которых существуют аналитические продолжения в области с при .

Будем считать также, что в пространстве определена метрика

.

Тогда справедлива

Теорема. При любых и для -энтропии метрического пространства имеет место соотношение эквивалентности

~ .

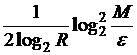
Доказательство. По основной теореме об энтропиях для фиксированных и при любом выполняется неравенство

.

Более того, если на отрезке определить вспомогательные пространства рядов по полиномам Чебышева

,

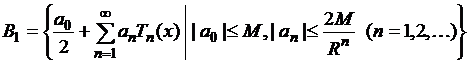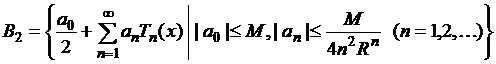
то по леммам 1 и 2 из предыдущего параграфа получим (заметим, что на этих пространствах определена одна и та же метрика). Отсюда в силу монотонности по множеству -емкости и -энтропии имеем

, .

Для оценки построим -сеть для . Для этого, исходя из полиномов Чебышева (), при фиксированных и натуральном (значения и подберем ниже) построим полиномы вида

,

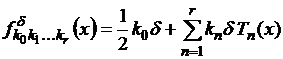где - некоторые целые числа. Эти числа подбираем экономно так, чтобы полиномы принадлежали .

Для этого достаточно потребовать выполнения следующих условий:

,

(),

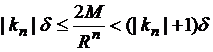а значит, должны выполняться неравенства

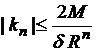, (). (1)

Выясним теперь, при каких значениях и семейство образует -сеть для множества .

Возьмем из пространства произвольный ряд

.

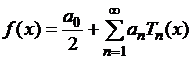Подберем целые числа () так, чтобы выполнялось неравенство

.

Тогда для с такими получим

.

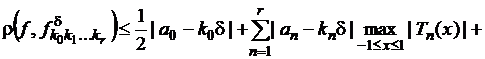
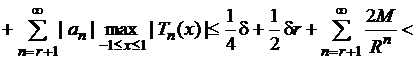
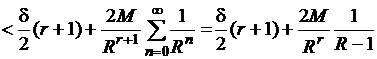Выберем и так, чтобы и 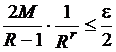. Тогда

, .

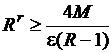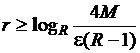Значит, можно взять , , 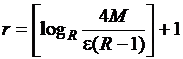чтобы получить

,

т.е. чтобы семейство полиномов образовало -сеть для пространства .

Оценим теперь минимальное число элементов в -сети для . Для этого воспользуемся неравенствами (1). Количество элементов в семействе равно количеству различных упорядоченных наборов целых чисел (), удовлетворяющих неравенствам (1). Их же количество, очевидно, не превосходит произведения

.

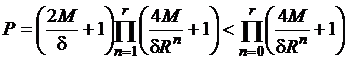В силу достаточной малости можно считать, что . Тогда

.

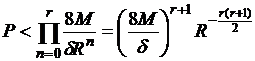Следовательно, подставив значения , 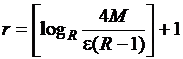и сохранив главные члены в оценках, получим

().

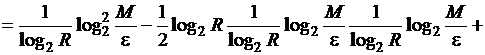
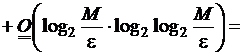
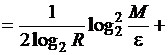
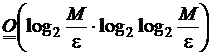Оценим теперь снизу , построив -цепь из элементов , а именно из полиномов вида

,

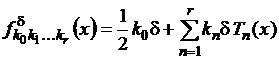причем , натуральное и целые коэффициенты подберем ниже так, чтобы в этой -цепи количество элементов получилось достаточно близким к количеству элементов максимальной -цепи множества .

Так как , должны выполняться неравенства

, ().

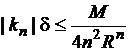Выберем их так, чтобы выполнялись еще неравенства

, (),

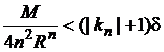а значит, неравенства

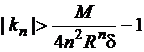, (). (2)

Чтобы элементы при условии (2) образовали -цепь, для любых двух различных элементов и из них должно выполняться неравенство . Разность этих элементов представляет собой некоторый полином вида

,

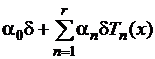в котором коэффициенты целые и не все равны нулю. Пусть является отличным от нуля коэффициентом с максимальным номером. Тогда, так как 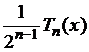при представляет собой наименее уклоняющийся от нуля полином степени со старшим коэффициентом единица, получим .

Согласно неравенствам (2), количество элементов в максимальной -цепи множества будет больше произведения

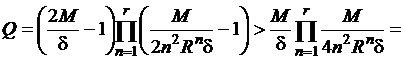
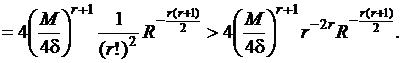
Значит,

.

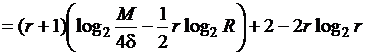Выберем и .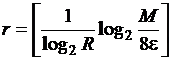

Тогда

.

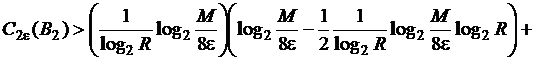
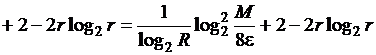Следовательно, отсюда и из полученной выше оценки сверху для имеем

~ .

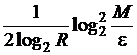
Теорема доказана.

Замечание. Из доказательства теоремы А.Г. Витушкина видно, что главный член -энтропии выделен с помощью разложений функций в ряды Фурье-Чебышева. Значит, запоминание коэффициентов Фурье-Чебышева аналитических на отрезке функций оказывается почти наилучшим способом экономии памяти для записи (табулирования) этих функций.