Оглавление

4. Энтропия и емкость

Пусть – данное метрическое пространство и пусть – предкомпактное множество из . Тогда (независимо от полноты ) вполне ограничено. Поэтому при для в существует конечная -сеть, скажем, . Количество этих точек зависит от того, как выбрать точки (даже при фиксированном ). Но следующая величина уже является инвариантом множества (т.е. не зависит от способа выбора точек при каждом фиксированном и фиксированном ):

(т.е. берется минимальное число точек в -сети из для ; если метрическое расширение для поменять, то ясно, что может меняться, так как точки берутся из ).

Чтобы закодировать множество с числом точек с помощью двоичных кодов наиболее экономным способом (т.е. чтобы объем таблицы был минимальным), нужно взять коды длины

.

Эта величина называется -энтропией множества относительно (А.Г. Витушкин). До нее А.Н. Колмогоров ввел понятие метрической энтропии, которая называется также абсолютной -энтропией множества . Эта величина уже не зависит от метрического расширения для множества , сохраняющего метрику .

Определим метрическую энтропию.

Пусть – предкомпактное подмножество . Тогда вполне ограничено и для него при любом заданном существует конечная -сеть из .

Возьмем замкнутые шары

.

Тогда они имеют и (вместе) образуют -покрытие множества .

Как и выше, число , вообще говоря, зависит от выбора точек , но следующая величина является инвариантным для :

.

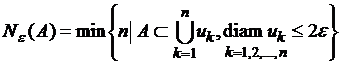В этом случае длина двоичного кода (для количества точек ) и называется метрической энтропией множества (по Колмогорову).

Относительная и абсолютная энтропии множества тесно связаны между собой и еще с одной величиной, которая называется - емкостью множества и определяется следующим образом.

Пусть – предкомпактное подмножество . Тогда при любом фиксированном множество может содержать только конечные -цепи (т.е. -различимые подмножества).

Действительно, допустим, что при некотором множество содержит некоторую бесконечную -цепь В силу предкомпактности эта последовательность должна иметь хотя бы одну предельную точку в . Пусть, например, . Тогда из неравенства

вытекает, что при чего не может быть, так как и суть элементы -цепи и (для фиксированного ).

Итак, при фиксированном любая -цепь из конечна, но число точек в -цепи может меняться при изменении элементов цепи .

Однако следующая величина не зависит от выбора этих точек (она – инвариант для и не зависит от его метрического расширения):

.

Длина двоичного кода для наиболее экономных таблиц с элементами равна

и называется -емкостью множества .

Очевидно, все три величины , и являются возрастающими функциями по и убывающими функциями по . Другими словами, например, всегда для подмножеств множества из следует (при любом фиксированном ) и всегда из следует (при любом фиксированном ).