Оглавление
3. Сети, цепи и покрытия
множеств
Пусть ![]() – некоторое
метрическое пространство,
– некоторое
метрическое пространство, ![]() и
и ![]() – заданное число.
– заданное число.
1) Множество ![]() называется
называется ![]() -сетью
для
-сетью
для ![]() (в
(в ![]() ), если
), если ![]() .
.
2) Множество ![]() называется
называется ![]() - различимым (в
- различимым (в ![]() ), если
), если ![]() .
.
Если множество ![]() является
является ![]() - различимым в
- различимым в ![]() , то это множество
, то это множество ![]() называется
называется ![]() -цепью в
-цепью в ![]() .
.
3) Система множеств ![]() называется
называется ![]() -покры-тием данного
множества
-покры-тием данного
множества ![]() , если:
, если:
а) ![]() ; б)
; б) ![]()
![]() .
.
Пример
1. Пусть ![]() – множество
действительных чисел,
– множество
действительных чисел, ![]() . Тогда
. Тогда ![]() будет метрическим
пространством (как известно, полным).
будет метрическим
пространством (как известно, полным).
Ясно, что множество ![]() будет
будет ![]() -сетью для
-сетью для ![]() (для
(для ![]() ) при
) при ![]() (и, естественно, при
(и, естественно, при ![]() ).
).
Множество ![]() будет
будет ![]() -различимым (т.е.
-различимым (т.е. ![]() -цепью) в
-цепью) в ![]() при всех
при всех ![]() .
.
При ![]() система интервалов
система интервалов 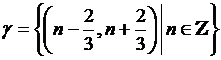 будет
будет ![]() -покрытием для
-покрытием для ![]() (и для
(и для ![]() ).
).
Пример
2. Пусть ![]() – двумерное евклидово
пространство, на котором задана метрика в виде:
– двумерное евклидово
пространство, на котором задана метрика в виде:
1) ![]() ;
;
2) ![]()
(здесь
![]() ,
, ![]() ). В
). В ![]() рассмотрим
множество
рассмотрим
множество ![]() и множество
и множество
![]() .
.
а) Для указанных двух метрик выяснить,
образует ли ![]() -сеть (и при каких
-сеть (и при каких ![]() ) множество
) множество ![]() для множества
для множества ![]() .
.
б) При каких ![]() множество
множество ![]() является
является ![]() -цепью в
-цепью в ![]() ?
?
в) Построить ![]() -покрытие (какое-нибудь) для множества
-покрытие (какое-нибудь) для множества ![]() (в каждой из указанных
метрик).
(в каждой из указанных
метрик).
Оказывается, следующие три свойства множеств
![]() в данном метрическом
пространстве
в данном метрическом
пространстве ![]() эквивалентны между
собой:
эквивалентны между
собой:
1) При любом ![]() существует конечное
существует конечное ![]() -покрытие множества
-покрытие множества ![]() .
.
2) При любом ![]() существует конечная
существует конечная ![]() -сеть для множества
-сеть для множества ![]() .
.
3) При любом ![]() любое
любое ![]() -различимое подмножество из
-различимое подмножество из ![]() конечно (т.е. при
любом
конечно (т.е. при
любом ![]() любая
любая ![]() -цепь из
-цепь из ![]() конечна).
конечна).