§ 3. Свойства измеримых по Лебегу множеств
Измеримость множеств и свойства
измеримых множеств тесно связаны с измеримостью их дополнения до некоторого
промежутка.
Дополнением
множества ![]() до данного промежутка
до данного промежутка ![]() (конечного или
бесконечного), содержащего
(конечного или
бесконечного), содержащего ![]() , называется множество
, называется множество ![]() .
.
Теорема
1. Множество ![]() измеримо тогда и
только тогда, когда его дополнение
измеримо тогда и
только тогда, когда его дополнение ![]() измеримо (дополнение
измеримо (дополнение ![]() берется до любого
данного конечного промежутка, содержащего
берется до любого
данного конечного промежутка, содержащего ![]() ).
).
Доказательство.
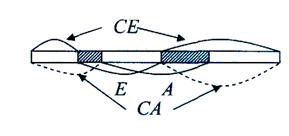
Для двух данных множеств ![]() и
и ![]() выполняется равенство
выполняется равенство ![]() (см.
рисунок ниже). Если при этом
(см.
рисунок ниже). Если при этом ![]() - элементарное множество, то его дополнением (до конечного
промежутка) также служит некоторое элементарное множество. Поэтому измеримость дополнения
- элементарное множество, то его дополнением (до конечного
промежутка) также служит некоторое элементарное множество. Поэтому измеримость дополнения ![]() до данного конечного
промежутка вытекает из неравенства
до данного конечного
промежутка вытекает из неравенства
![]() (
(![]() ).
).
Теорема
2.
Если множества ![]() и
и ![]() измеримы, то измеримы
множества
измеримы, то измеримы
множества ![]() ,
, ![]() ,
, ![]() и
и ![]() .
.
Доказательство. 1) Пусть ![]() - любое фиксированное
число и
- любое фиксированное
число и ![]() - элементарные
множества такие, что
- элементарные
множества такие, что ![]() ,
, ![]() . Тогда выполняется
соотношение
. Тогда выполняется
соотношение ![]() , т.к. в левой части от
, т.к. в левой части от ![]() отнимаем
отнимаем ![]() и
и ![]() , а в правой части от
, а в правой части от ![]() отнимаем только
отнимаем только ![]() ; аналогично, в левой части от
; аналогично, в левой части от ![]() отнимаем
отнимаем ![]() и
и ![]() , а в правой части от
, а в правой части от ![]() отнимаем только
отнимаем только ![]() . Из этого соотношения следует, что
. Из этого соотношения следует, что ![]()
(мы
воспользовались монотонностью и полуаддитивностью
внешней меры).
2) Пусть ![]() - некоторый отрезок,
включающий множества
- некоторый отрезок,
включающий множества ![]() и
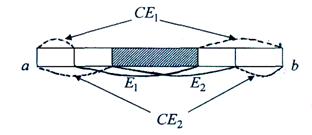
и ![]() . Тогда для дополнений до него получим
. Тогда для дополнений до него получим ![]() (см.
рисунок ниже). Остается применить доказанную измеримость объединения и теорему 1.
(см.
рисунок ниже). Остается применить доказанную измеримость объединения и теорему 1.
3)
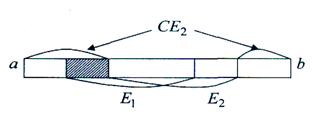
Пусть ![]() . Тогда измеримость разности
. Тогда измеримость разности ![]() вытекает из равенства
вытекает из равенства ![]() (см.
рисунок ниже).
(см.
рисунок ниже).
4)
Измеримость симметрической разности вытекает из измеримости разности, объединения
и следующего равенства: ![]() .
.
Следствие. Если множества ![]() измеримы, то измеримы
их объединение
измеримы, то измеримы
их объединение ![]() и их пересечение
и их пересечение ![]() .
.
Теорема 3.
Если множества ![]() измеримы, то измеримо
множество
измеримы, то измеримо
множество 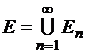 ; если при этом
; если при этом ![]() при всех
при всех ![]() , то выполняется равенство
, то выполняется равенство 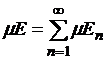 (счетная
аддитивность меры Лебега); если же
(счетная
аддитивность меры Лебега); если же ![]() , то измеримо множество
, то измеримо множество 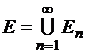 и выполняется равенство
и выполняется равенство ![]() .
.
Теорема 4.
Если множества ![]() измеримы, то измеримо
множество
измеримы, то измеримо
множество 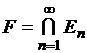 ; если при этом
; если при этом ![]() , то выполняется равенство
, то выполняется равенство
![]() (непрерывность меры
Лебега).
(непрерывность меры
Лебега).
Доказательства теорем 3 и 4 можно
найти в [2].
Оглавление