§ 2. Линейная мера Лебега
Прежде всего
отметим, что наряду с объединением и пересечением над множествами определяются
также две операции вычитания.
Разностью ![]() двух множеств
двух множеств ![]() и
и ![]() называется множество,
каждый элемент которого принадлежит множеству
называется множество,
каждый элемент которого принадлежит множеству ![]() и не принадлежит множеству
и не принадлежит множеству ![]() .
.
Симметрической
разностью двух множеств ![]() и
и ![]() называется множество
называется множество ![]() , равное объединению двух разностей
, равное объединению двух разностей ![]() и
и ![]() .
.

Заметим, что если мысленно
двигать множества ![]() и
и ![]() относительно друг
друга, то ясно, что чем меньше симметрическая разность двух данных множеств
(т.е. площадь заштрихованной части), тем больше их пересечение (площадь общей
части этих множеств), а значит, тем «ближе» эти множества друг к другу. Этим свойством симметрической разности
мы воспользуемся для «измерения» множеств, а начнем с обобщения понятия
конечного промежутка и определения его меры.
относительно друг
друга, то ясно, что чем меньше симметрическая разность двух данных множеств
(т.е. площадь заштрихованной части), тем больше их пересечение (площадь общей
части этих множеств), а значит, тем «ближе» эти множества друг к другу. Этим свойством симметрической разности
мы воспользуемся для «измерения» множеств, а начнем с обобщения понятия
конечного промежутка и определения его меры.
Промежутком ![]() будем называть любое
из следующих множеств:
будем называть любое
из следующих множеств: ![]() - интервал,
- интервал, ![]() - сегмент,
- сегмент, ![]()
![]() - полуинтервалы,
причем, если не оговорено противное, будем считать
- полуинтервалы,
причем, если не оговорено противное, будем считать ![]() и
и ![]() действительными числами и необязательно
действительными числами и необязательно ![]() . Будем считать промежуток
. Будем считать промежуток ![]() пустым множеством
пустым множеством ![]() , если
, если ![]() , или если
, или если ![]() , а промежуток
, а промежуток ![]() представляет собой интервал
представляет собой интервал
![]() или один из полуинтервалов
или один из полуинтервалов ![]() и
и ![]() .
.
Множество ![]() называется элементарным, если его можно представить
в виде конечного объединения некоторых промежутков:
называется элементарным, если его можно представить
в виде конечного объединения некоторых промежутков:
![]() .
.
Мерой промежутка ![]() называется его длина
называется его длина ![]() ; если
; если ![]() , то
, то ![]() .
.
Внешней
мерой ограниченного множества ![]() назовем величину
назовем величину
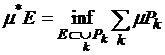 ,
,
где инфимум берется по всем конечным или счетным покрытиям
множества ![]() промежутками
промежутками ![]()
Заметим, что любое ограниченное
множество ![]() имеет конечную внешнюю меру.
имеет конечную внешнюю меру.
Действительно, для такого множества ![]() существует покрытие из
одного промежутка
существует покрытие из
одного промежутка ![]() ; при этом множество сумм
; при этом множество сумм
![]() ограничено снизу нулем.
ограничено снизу нулем.
Отметим два важных свойства внешних мер:
1) монотонность: из
![]() следует
следует ![]() (т.к. для покрытия
(т.к. для покрытия ![]() нужны дополнительные
промежутки);
нужны дополнительные
промежутки);
2) полуаддитивность: ![]() (т.к. если
(т.к. если ![]() , то промежутки для его покрытия в правой части могут
встречаться два раза).
, то промежутки для его покрытия в правой части могут
встречаться два раза).
Множество ![]() называется измеримым
по Лебегу, если для
называется измеримым
по Лебегу, если для ![]() существует элементарное множество
существует элементарное множество
![]() такое, что
такое, что ![]() . Если множество
. Если множество ![]() измеримо по Лебегу, то
мерой множества
измеримо по Лебегу, то
мерой множества ![]() по Лебегу называется
его внешняя мера:
по Лебегу называется
его внешняя мера:
![]() .
.
Значит, измеримые множества - это множества, близкие к элементарным
множествам: они сколь угодно мало отличаются от элементарных множеств (в смысле
внешней меры).
Простейшим примером измеримого
множества служит любое конечное множество ![]() .
.
Действительно, в качестве
элементарного множества ![]() при
при
![]() можно взять само
множество
можно взять само
множество ![]() , так как
, так как
![]() .
.
Тогда
из ![]() следует, что
следует, что ![]() . Очевидно,
. Очевидно, ![]()
Замечание 1. Меру Лебега можно распространить и на случай
неограниченных множеств ![]() . Такое множество
. Такое множество ![]() называется измеримым, если измеримо любое множество
вида
называется измеримым, если измеримо любое множество
вида ![]() (
(![]() - натуральное число). Мерой множества
- натуральное число). Мерой множества ![]() в этом случае
называется следующий предел:
в этом случае
называется следующий предел: ![]() =
=![]() (который может равняться и
(который может равняться и ![]() ).
).
Замечание 2. Если в определении внешней
меры сохранить лишь конечные покрытия ограниченного множества ![]() промежутками, то по
аналогии с мерами Лебега получим внешнюю
меру Жордана
промежутками, то по
аналогии с мерами Лебега получим внешнюю
меру Жордана ![]() и меру Жордана
и меру Жордана ![]() множества
множества ![]() .
.
Отметим, что мера Лебега является
существенно более широким понятием, чем мера Жордана.
Например, лебегова мера множества рациональных чисел
равна нулю, в то время как это множество не является измеримым по Жордану.
Оглавление