§ 14. Задания для самостоятельной подготовки
Задача 1.
Найти меру Лебега ![]() , если:
, если:
1) 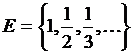 . (0)
. (0)
2) 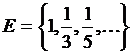 . (0)
. (0)
3) 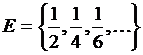 . (0)
. (0)
4) 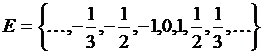 . (0)
. (0)
5) 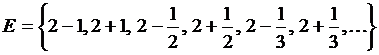 . (0)
. (0)
6) ![]() - множество всех
рациональных чисел из отрезка
- множество всех
рациональных чисел из отрезка ![]() . (0)
. (0)
7) ![]() - множество всех
иррациональных чисел из отрезка
- множество всех
иррациональных чисел из отрезка ![]() . (1)
. (1)
8) 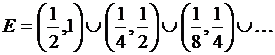 (1)
(1)
9) 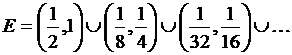
![]()
10) 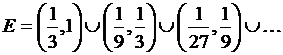 (1)
(1)
11) 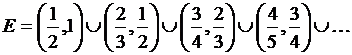 (1)
(1)
Задача 2. Эквивалентны
ли данные множества:
1)
Промежутки ![]() и
и ![]() ? (да)
? (да)
2) Множество
всех рациональных чисел и интервал ![]() ? (нет)
? (нет)
3)
Множество ![]() и множество
и множество ![]() ? (нет)
? (нет)
4)
Множество ![]() (действительных чисел)
и множество
(действительных чисел)
и множество ![]() (рациональных чисел)?
(нет)
(рациональных чисел)?
(нет)
Задача 3. 1)
Верно ли, что множество рациональных
чисел и множество натуральных чисел имеют одинаковую мощность? (да)
2)
Найти мощность множества ![]() . (10)
. (10)
Задача 4. Является ли элементарным
данное множество:
1) Множество ![]() ? (да)
? (да)
2)
Пустое множество? (да)
3)
Множество всех натуральных чисел? (нет)
Задача 5. Выберите
все верные варианты ответов:
1)
Внешняя мера Лебега ограниченного множества E равна инфимуму
суммы мер (длин) промежутков, составляющих покрытие множества E, причем инфимум
берется по всем…
а)
конечным или счетным покрытиям;
б)
конечным покрытиям;
в)
конечным или бесконечным покрытиям;
г)
счетным покрытиям.
2)
Любое ограниченное множество имеет…
а)
конечную внешнюю меру Лебега;
б)
конечную меру Лебега;
в)
мощность множества всех натуральных чисел;
г)
мощность множества всех рациональных чисел.
3)
Ограниченное множество называется измеримым по Лебегу, если…
а)
внешнюю меру его симметрической разности с элементарным множеством можно
сделать сколь угодно малой за счет выбора элементарного множества; б) оно
эквивалентно счетному множеству;
в)
оно эквивалентно некоторому элементарному множеству.
4) Для множества 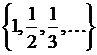 …
…
а)
меры Лебега и Жордана равны;
б)
мера Лебега больше меры Жордана;
в)
мера Жордана не существует, мера Лебега существует;
г)
мера Лебега меньше меры Жордана.
5)
Для множества всех рациональных чисел из ![]() …
…
а) мера
Жордана не существует, мера Лебега равна нулю;
б)
меры Лебега и Жордана равны;
в)
мера Лебега больше меры Жордана;
г)
мера Лебега меньше меры Жордана.
6)
Любое ограниченное…
а)
открытое множество измеримо по Лебегу;
б) замкнутое
множество измеримо по Лебегу;
в) замкнутое
множество измеримо по Лебегу, открытое
не всегда.
Задача 6. Выберите
все верные варианты ответов:
1) Функция ![]() , определенная на множестве
, определенная на множестве![]() , называется измеримой (по Лебегу), если…
, называется измеримой (по Лебегу), если…
а)
множества ![]() и
и ![]() при всех
при всех ![]() измеримы;
измеримы;
б)
множество ![]() измеримо, функция
измеримо, функция ![]() ограничена;
ограничена;
в)
множество ![]() измеримо, функция
измеримо, функция ![]() непрерывна;
непрерывна;
г)
множество ![]() измеримо.
измеримо.
2)
Функция ![]() на множестве
на множестве ![]() …
…
а)
измерима; б) непрерывна; в) ограничена; г) непрерывна и ограничена.
3)
Неверно, что на данном отрезке ![]() …
…
а)
измеримая функция всегда непрерывна;
б)
измеримая функция всегда ограничена;
в)
функция Дирихле ![]() , разрывная во всех точках, измерима;
, разрывная во всех точках, измерима;
г)
измеримая функция может быть ограничена.
4)
Если мера Лебега множества ![]() равна нулю, то…
равна нулю, то…
а)
любая определенная на ![]() функция измерима;
функция измерима;
б)
функция измерима, если только она ограничена;
в)
функция измерима на ![]() , если только она непрерывна;
, если только она непрерывна;
г)
функция измерима на ![]() , если только она непрерывна и ограничена.
, если только она непрерывна и ограничена.
5)
Если две функции![]() и
и ![]() измеримы на данном
множестве
измеримы на данном
множестве ![]() , то не всегда на
, то не всегда на ![]() …
…
а)
функция ![]() измерима; б) функции
измерима; б) функции ![]() измеримы;
измеримы;
в)
функция ![]() измерима; г) функция
измерима; г) функция ![]() измерима.
измерима.
6)
Если две функции![]() и
и ![]() неизмеримы на данном
измеримом множестве
неизмеримы на данном
измеримом множестве ![]() , то всегда…
, то всегда…
а) ![]() неизмерима;
неизмерима;
б) ![]() неизмерима;
неизмерима;
в) ![]() неизмерима; г)
неизмерима; г) ![]() неизмерима.
неизмерима.
Задача 7. Выберите
все верные варианты ответов:
1)
Функция Дирихле ![]() , равная 1 в рациональных точках и равная 0 в иррациональных
точках, на любом отрезке
, равная 1 в рациональных точках и равная 0 в иррациональных
точках, на любом отрезке ![]() …
…
а) эквивалентна тождественному нулю;
б) эквивалентна тождественной единице;
в)
не эквивалентна никакой непрерывной функции.
2)
Неверно, что функция ![]() на отрезке
на отрезке ![]() …
…
а) эквивалентна постоянной функции;
б)
непрерывна почти всюду;
в)
дифференцируема почти всюду.
3)
Неверно, что …
а)
функция Дирихле ![]() , равная 1 в рациональных точках и равная 0 в иррациональных
точках, непрерывна почти всюду на отрезке
, равная 1 в рациональных точках и равная 0 в иррациональных
точках, непрерывна почти всюду на отрезке ![]() ;
;
б)
предел функции ![]() при
при
![]() почти всюду на
отрезке
почти всюду на
отрезке ![]()
равен
нулю;
в)
функция ![]() почти всюду на
отрезке [-1,1] дифференцируема.
почти всюду на
отрезке [-1,1] дифференцируема.
Задача 8.
Выберите все верные варианты ответов:
1)
Неверно, что для любой ограниченной измеримой на данном отрезке ![]() функции
функции ![]() всегда …
всегда …
а)
интеграл Римана 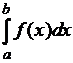 существует;
существует;
б)
интеграл Лебега 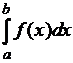 существует;
существует;
в) супремум всех нижних сумм Лебега равен инфимуму всех
верхних сумм Лебега;
г)
интегралы Римана и Лебега существуют.
2)
При составлении сумм Лебега произвольной ограниченной измеримой функции ![]() …
…
а)
берутся разбиения по оси ![]() ; б) можно взять разбиения по оси
; б) можно взять разбиения по оси ![]() ;
;
в)
берутся разбиения и по оси ![]() , и по оси
, и по оси ![]() .
.
3) Неверно,
что для любой ограниченной измеримой на данном отрезке ![]() (
(![]() ) функции
) функции ![]() …
…
а)
интегралы Римана и Лебега совпадают;
б) супремум нижних сумм Лебега равен
интегралу Лебега;
в) инфимум верхних сумм Лебега равен
интегралу Лебега;
г)
интеграл Лебега 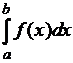 существует.
существует.
4)
Неверно, что для интегралов Лебега всегда …
а) из
существования ![]() вытекает существование
вытекает существование
![]() ;
;
б) из ![]() при
при ![]() вытекает
вытекает ![]() (если интегралы
существуют);
(если интегралы
существуют);
в) ![]() (если интегралы
существуют;
(если интегралы
существуют;![]() ).
).
5)
Две измеримые на данном множестве ![]() функции
функции ![]() и
и ![]() называются
эквивалентными, если…
называются
эквивалентными, если…
а)
мера Лебега множества ![]() равна нулю;
равна нулю;
б)
эквивалентны множества значений этих функций;
в)
интегралы Лебега от этих функций равны.
6)
Если (собственный) интеграл Римана 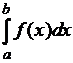 существует, то…
существует, то…
а) он
равен интегралу Лебега 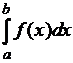 ;
;
б) ![]() может быть
неограниченной, а потому неинтегрируемой по Лебегу; в)
может быть
неограниченной, а потому неинтегрируемой по Лебегу; в) ![]() может быть
неизмеримой, а потому неинтегрируемой по Лебегу.
может быть
неизмеримой, а потому неинтегрируемой по Лебегу.
7)
Если функция ![]() дифференцируема на
данном отрезке
дифференцируема на
данном отрезке ![]() и ее производная
и ее производная ![]() ограничена на нем,
то
ограничена на нем,
то 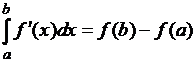 …
…
а) всегда
для интеграла Лебега и не всегда для интеграла Римана;
б)
всегда для интеграла Римана и не всегда для интеграла Лебега;
в)
не всегда как для интеграла Лебега, так и для интеграла Римана;
г)
всегда для интеграла Римана и для интеграла Лебега.
8)
Для неограниченной на данном множестве ![]() функции
функции ![]()
интеграл
Лебега 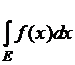 …
…
а)
определяется как ![]() , если только
, если только ![]() и измерима на
и измерима на ![]() ;
;
б)
вообще не определяется;
в)
определяется как ![]() в случае любой
измеримой на
в случае любой
измеримой на ![]()
функции
![]() .
.
9)
Не всегда верно, что для положительной ![]() и отрицательной
и отрицательной ![]() частей функции
частей функции ![]() выполняются
соотношения …
выполняются
соотношения …
а) ![]() ;
;
б) ![]() ;
;
в) ![]() .
.
10)
Интегралом Лебега 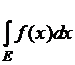 от (произвольной)
измеримой на данном множестве
от (произвольной)
измеримой на данном множестве ![]() функции
функции ![]() называется разность
интегралов
называется разность
интегралов
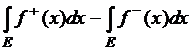 , если …
, если …
а) хотя бы один из этих интегралов конечен;
б) только оба интеграла конечны; в) даже оба
интеграла бесконечны.
11)
Функция ![]() называется
интегрируемой по Лебегу (или суммируемой) на данном множестве
называется
интегрируемой по Лебегу (или суммируемой) на данном множестве ![]() ,…
,…
а)
если только интеграл ![]() конечен;
конечен;
б)
если хотя бы один из интегралов 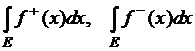 конечен;
конечен;
в)
если только функция ![]() ограничена и измерима на
ограничена и измерима на ![]() .
.
12)
Из функций ![]() и
и ![]() равенству
равенству 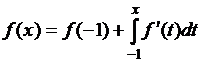 при всех
при всех ![]() удовлетворяют…
удовлетворяют…
а) обе
функции; б) только ![]() ; в) ни одна; г) только
; в) ни одна; г) только ![]() .
.
13)
Из функций ![]() и
и ![]() равенству
равенству 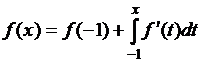 при всех
при всех ![]() удовлетворяют…
удовлетворяют…
а) ![]() ; б) обе функции; в) ни одна; г)
; б) обе функции; в) ни одна; г) ![]() .
.
14)
Функция ![]() , равная
, равная ![]() при
при
![]() и нулю при
и нулю при ![]() , на отрезке
, на отрезке ![]() …
…
а) не
является ни суммируемой (интегрируемой по Лебегу), ни интегрируемой по Риману в
несобственном смысле;
б)
является суммируемой и неинтегрируемой по Риману;
в)
является интегрируемой по Риману в несобственном смысле и не является
суммируемой.
15)
Функция Дирихле ![]() , равная 1 в рациональных точках и равная 0 в иррациональных
точках, на отрезке
, равная 1 в рациональных точках и равная 0 в иррациональных
точках, на отрезке ![]() …
…
а)
является суммируемой (интегрируемой по Лебегу) и неинтегрируемой по Риману (в
собственном или несобственном смысле);
б)
является суммируемой и интегрируемой по Риману в несобственном смысле;
в)
не является ни суммируемой, ни интегрируемой по Риману.
16)
Функция ![]() , равная
, равная ![]() при
при
![]() и нулю при
и нулю при ![]() , на отрезке
, на отрезке ![]() …
…
а) является
суммируемой (интегрируемой по Лебегу) и интегрируемой по Риману в несобственном
смысле;
б)
не является суммируемой и является интегрируемой по Риману в несобственном
смысле;
в)
не является суммируемой и интегрируемой
по Риману.
17)
Неверно, что на отрезке ![]() …
…
а)
всегда ограниченная измеримая функция интегрируема по Риману;
б)
функция ![]() , равная
, равная ![]() при
при
![]() и нулю при
и нулю при ![]() измерима, но не
интегрируема по Лебегу;
измерима, но не
интегрируема по Лебегу;
в)
всегда функции ![]() и
и ![]() одновременно
интегрируемы по Лебегу или нет, если
одновременно
интегрируемы по Лебегу или нет, если ![]() измерима.
измерима.
Задача 9.
Найти интеграл Лебега:
1) 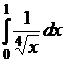 .
. ![]()
2) 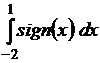 . (-1)
. (-1)
3) 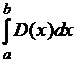 , где
, где ![]() - функция Дирихле,
равная 1 в рациональных точках и 0 в иррациональных точках. (0)
- функция Дирихле,
равная 1 в рациональных точках и 0 в иррациональных точках. (0)
4) ![]() , где
, где ![]() – множество всех
рациональных точек отрезка
– множество всех
рациональных точек отрезка ![]() . (0)
. (0)
5) 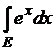 , где
, где 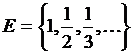 . (0)
. (0)
6) 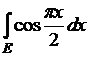 , где
, где ![]() – множество всех
иррациональных точек отрезка
– множество всех
иррациональных точек отрезка ![]() .
. ![]()
7) 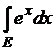 , где
, где 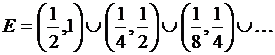 (
(![]() -1)
-1)
8) ![]() , где
, где 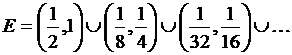 (4)
(4)
9) 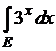 , где
, где 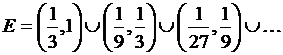
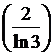
10) ![]() , где
, где 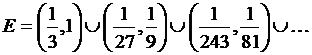 (3)
(3)
11) 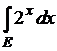 , где
, где 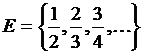 . (0)
. (0)
12) 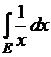 , где
, где 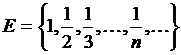 . (0)
. (0)
13) 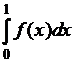 , где функция
, где функция ![]() равна
равна ![]() в рациональных точках
и равна
в рациональных точках
и равна ![]() в иррациональных
точках.
в иррациональных
точках. ![]()
14) 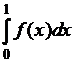 , где функция
, где функция ![]() равна
равна ![]() при
при
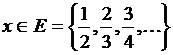 и
и ![]() при
при ![]() . (0)
. (0)
15) 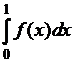 , где функция
, где функция ![]() равна 6 при
равна 6 при 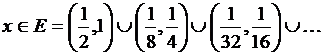 и 9 при
и 9 при ![]() . (7)
. (7)
16) 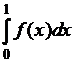 , где функция
, где функция ![]() равна 4 при
равна 4 при 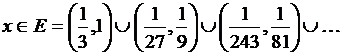 и 16 при
и 16 при ![]() . (7)
. (7)
17) 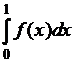 , где функция
, где функция ![]() равна
равна ![]() в иррациональных
точках и
в иррациональных
точках и ![]() в рациональных точках
отрезка
в рациональных точках
отрезка ![]() . (2)
. (2)