§10. Сравнение интегралов Римана и Лебега для ограниченных функций
Выясним
сначала, какой из этих двух интегралов определен на более широком классе
функций, заданных на данном
отрезке.
Как
известно, если ![]() непрерывна
на отрезке
непрерывна
на отрезке ![]() , то существует
, то существует 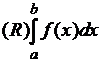 . Однако существуют разрывные функции, интегрируемые по
Риману, которые могут иметь бесконечное множество точек разрыва. При этом, как
доказал А. Лебег, точек разрыва не должно быть много в смысле меры.
Точнее, для существования
. Однако существуют разрывные функции, интегрируемые по
Риману, которые могут иметь бесконечное множество точек разрыва. При этом, как
доказал А. Лебег, точек разрыва не должно быть много в смысле меры.
Точнее, для существования 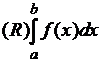 от ограниченной на
отрезке
от ограниченной на
отрезке ![]() функции
функции ![]() необходимо и
достаточно, чтобы мера (Лебега) множества ее точек разрыва на этом отрезке равнялась нулю.
необходимо и
достаточно, чтобы мера (Лебега) множества ее точек разрыва на этом отрезке равнялась нулю.
Вместе
с тем, существует всюду разрывная на данном отрезке ![]() (
(![]() ) функция Дирихле
) функция Дирихле ![]() , интегрируемая по Лебегу и неинтегрируемая по Риману.
, интегрируемая по Лебегу и неинтегрируемая по Риману.
Значит,
даже для ограниченных на данном отрезке функций из существования интеграла
Лебега не следует существование интеграла Римана.
Оказывается,
справедливо обратное утверждение.
Теорема. Если
функция ![]() интегрируема в смысле
Римана на данном отрезке
интегрируема в смысле
Римана на данном отрезке ![]() , то она интегрируема на этом отрезке и в смысле Лебега,
причем выполняется равенство
, то она интегрируема на этом отрезке и в смысле Лебега,
причем выполняется равенство 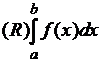 =
= 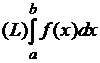 .
.
Доказательство. Из
интегрируемости функции ![]() по Риману на данном
отрезке
по Риману на данном
отрезке ![]() вытекает ее ограниченность
на этом отрезке. Поэтому остается доказать измеримость
вытекает ее ограниченность
на этом отрезке. Поэтому остается доказать измеримость ![]() на
на
![]() . Для этого возьмем
последовательность равномерных разбиений:
. Для этого возьмем
последовательность равномерных разбиений:
![]()
![]() (
(![]() ).
).
Тогда шаг разбиения ![]() и
и ![]() равносильно
равносильно ![]() .
.
Построим
две последовательности функций. Для каждого разбиения ![]() построим свои две
функции
построим свои две
функции ![]() и
и ![]() следующим образом: при
следующим образом: при ![]() положим
положим ![]() ,
, ![]() .
.
Пусть
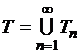 - множество всех точек
разбиений; оно счетно, поэтому
- множество всех точек
разбиений; оно счетно, поэтому ![]() . В каждой другой точке
. В каждой другой точке ![]() последовательность
последовательность ![]() возрастает, а
последовательность
возрастает, а
последовательность ![]() убывает при
убывает при ![]() . Отсюда следует, что существуют
. Отсюда следует, что существуют ![]() ,
, ![]() .
.
Так
как при всех ![]() выполняется
неравенство
выполняется
неравенство ![]() , то получим
, то получим ![]() , откуда следует, что
, откуда следует, что ![]() .
.
Заметим,
что ![]() и
и ![]() ограниченные
последовательности функций (одним и тем же числом для всех
ограниченные
последовательности функций (одним и тем же числом для всех ![]() и всех натуральных
и всех натуральных ![]() ). Поэтому последовательность
). Поэтому последовательность ![]() также ограничена.
Функции
также ограничена.
Функции ![]() и
и ![]() измеримы (как ступенчатые функции), поэтому их
разность
измеримы (как ступенчатые функции), поэтому их
разность ![]() также измерима.
также измерима.
Следовательно,
можно перейти к пределу под знаком интеграла
(по свойствам интеграла Лебега): 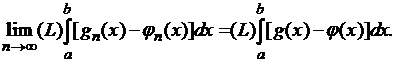
С
другой стороны, имеем 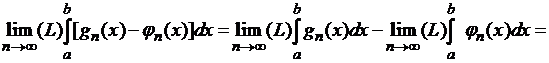
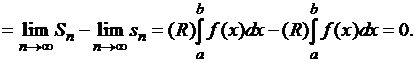
Следовательно, ![]() почти всюду на
почти всюду на ![]() , а значит,
, а значит,
![]() почти всюду на
почти всюду на ![]() .
.
Итак,
![]() является измеримой на
является измеримой на ![]() функцией. Раз
функцией. Раз ![]() ограничена
и измерима, то существует
ограничена
и измерима, то существует 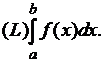
Далее, 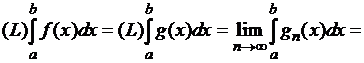
 Теорема доказана.
Теорема доказана.
Выясним
теперь, как обстоит дело с восстановлением функции по ее производной или как
основная теорема интегрального исчисления работает в случае интеграла Римана и
как - в случае интеграла Лебега.
Для
интеграла Римана основная теорема интегрального исчисления формулируется в различных формах. Речь идет о
формуле Ньютона-Лейбница:
 (1)
(1)
где ![]() - первообразная
функции
- первообразная
функции ![]() на отрезке
на отрезке ![]() , т.е.
, т.е. ![]() для всех
для всех ![]() .
.
Для
интегралов Римана это равенство часто может не выполняться. Например, возможны
случаи:
1)
функция ![]() может быть
интегрируемой по Риману, но для нее не существует первообразная
может быть
интегрируемой по Риману, но для нее не существует первообразная ![]() (на отрезке
(на отрезке ![]() );
);
2)
для функции ![]() может существовать
первообразная
может существовать
первообразная ![]() , но сама функция
, но сама функция ![]() может быть
неинтегрируемой по Риману, даже если
может быть
неинтегрируемой по Риману, даже если ![]() существует во всех
существует во всех
![]() и ограничена.
и ограничена.
Следовательно,
интеграл Римана не решает вопрос о восстановлении функции по ее производной
даже в случае ограниченности производных.
В случае интеграла
Лебега имеет место
Теорема. Если производная ![]() существует во всех
точках отрезка
существует во всех
точках отрезка ![]() и она ограничена на
этом отрезке, то выполняется равенство
и она ограничена на
этом отрезке, то выполняется равенство 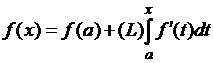 для всех
для всех ![]() ; в частности, при
; в частности, при ![]() получим равенство
получим равенство 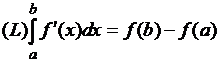 .
.
Доказательство. Сначала докажем требуемое равенство при ![]() . Раз существует конечная производная
. Раз существует конечная производная ![]() , то сама функция
, то сама функция ![]() непрерывна на отрезке
непрерывна на отрезке ![]() , а потому она измерима на
, а потому она измерима на ![]() . Саму производную можно представить в виде следующего
предела:
. Саму производную можно представить в виде следующего
предела:
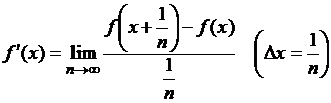 .
.
Раз
под знаком предела находится последовательность измеримых функций,
производная ![]() как предел измеримых
функций, будет измеримой функцией. По свойствам конечного предела функции
выполняется неравенство
как предел измеримых
функций, будет измеримой функцией. По свойствам конечного предела функции
выполняется неравенство  при всех
при всех ![]() , начиная с некоторого номера
, начиная с некоторого номера ![]() . Отсюда получим
. Отсюда получим 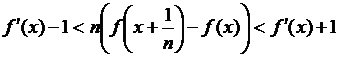 (
(![]() ), т.е. последовательность функций
), т.е. последовательность функций 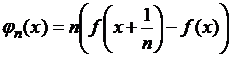 является ограниченной.
является ограниченной.
Следовательно,
можно перейти к пределу под знаком интеграла Лебега: 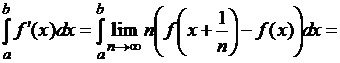

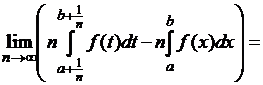
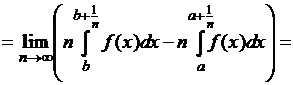
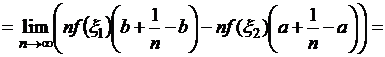
![]() .
.
Замечание. По ходу доказательства мы
функцию ![]() , определенную
, определенную
на отрезке ![]() , продолжаем на
отрезок
, продолжаем на
отрезок ![]() . Для этого достаточно считать, что
. Для этого достаточно считать, что ![]() при
при
![]() .
.
Итак,
теорема доказана при ![]() . Легко увидеть, что приведенные выше рассуждения применимы к
любому отрезку
. Легко увидеть, что приведенные выше рассуждения применимы к
любому отрезку ![]() .
.
Теорема полностью доказана.
Естественно,
возникает вопрос: как восстановить функцию по ее производной, если производная
оказывается неограниченной и точек неограниченности бесконечно много?
Для решения, в частности, и этой задачи
интеграл Лебега распространяется на неограниченные функции: сначала – на
неотрицательные функции, а затем – на функции любого знака.
Оглавление