§ 1. Сравнение множеств по мощности
Под множеством,
как обычно, будем понимать любую совокупность объектов, имеющих определенный
общий признак или обладающих определенным общим свойством. Сами объекты
называются элементами множества, причем каждый объект может
служить лишь одним элементом данного множества. Множество считается заданным,
если относительно любого данного объекта можно сказать, принадлежит он этому
множеству или не принадлежит.
Записи ![]() и
и ![]() соответственно
означают, что
соответственно
означают, что ![]() элемент множества
элемент множества ![]() , а
, а ![]() нет. Пустое
множество
нет. Пустое
множество ![]() не содержит ни одного
элемента.
не содержит ни одного
элемента.
Если каждый элемент множества ![]() является элементом
множества
является элементом
множества ![]() , то
, то ![]() называется подмножеством
называется подмножеством ![]() и пишут
и пишут ![]() . Если одновременно
. Если одновременно ![]() и
и ![]() , то множества
, то множества ![]() и
и ![]() называются равными:
называются равными: ![]() .
.
Два множества ![]() и
и ![]() называются эквивалентными,
если между ними можно установить взаимно однозначное соответствие, т.е. по некоторому
правилу каждому элементу
называются эквивалентными,
если между ними можно установить взаимно однозначное соответствие, т.е. по некоторому
правилу каждому элементу ![]() можно поставить в
соответствие элемент
можно поставить в
соответствие элемент ![]() и при этом каждый элемент
и при этом каждый элемент ![]() оказывается
поставленным в соответствие только
одному
оказывается
поставленным в соответствие только
одному ![]() . Эквивалентность обозначается так:
. Эквивалентность обозначается так: ![]() .
.
Заметим, что два конечных множества
эквивалентны тогда и только тогда, когда содержат одинаковое количество
элементов (в противном случае нарушается взаимная однозначность соответствия).
Если два множества равны, то они эквивалентны; но не всякие два эквивалентных
множества равны.
Если
два множества эквивалентны между собой, то говорят, что они имеют одинаковую мощность. Мощностью
конечного множества называют количество его элементов.
Множество
![]() называется счетным, если оно эквивалентно множеству
называется счетным, если оно эквивалентно множеству
![]() всех натуральных
чисел, т.е. если
всех натуральных
чисел, т.е. если ![]() или, другими словами,
если без повторений все элементы множества
или, другими словами,
если без повторений все элементы множества ![]() можно последовательно пронумеровать:
можно последовательно пронумеровать: ![]()
Например, множество всех четных чисел ![]() счетно.
счетно.
Действительно, взаимно однозначное
соответствие можно установить следующим
образом: ![]() .
.
Другой
пример: множество всех целых чисел ![]() счетно.
счетно.
В
самом деле, все целые числа можно пронумеровать, например, в следующей
последовательности: ![]()
Для
построения нового множества из данных множеств или представления одних множеств
через другие над множествами определяются операции объединения и пересечения.
Объединением
двух множеств ![]() и
и ![]() называется множество
называется множество ![]() , каждый элемент которого является элементом множества
, каждый элемент которого является элементом множества ![]() или множества
или множества ![]() .
.
Пересечением
двух множеств ![]() и
и ![]() называется множество
называется множество ![]() , каждый элемент
которого является элементом множества
, каждый элемент
которого является элементом множества ![]() и множества
и множества ![]() .
.

Аналогично
определяются объединение и пересечение трех и более множеств.
При
решении задач на множества часто используется следующее свойство не более чем счетных множеств.
Теорема 1. Как конечное, так и счетное объединение
конечных или счетных множеств конечно или счетно.
Для доказательства этого утверждения
можно построить прямоугольную таблицу, в строках которой последовательно
расположены элементы слагаемых данного объединения множеств. После этого
элементы полученной таблицы можно пронумеровать, начиная с верхнего левого угла
по побочным диагоналям.
Приведем
два примера на применение этой теоремы.
Счетность
множества всех рациональных чисел 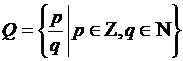 следует из теоремы 1,
если
следует из теоремы 1,
если ![]() представить в виде
представить в виде ![]() , где
, где ![]()

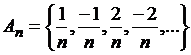 ,…
,…
(в множествах ![]() сохраняем только несократимые
дроби, не вошедшие в предыдущие множества
сохраняем только несократимые
дроби, не вошедшие в предыдущие множества ![]() ).
).
Как
известно, комплексное, в частности, действительное число называется алгебраическим,
если оно является корнем некоторого алгебраического уравнения ![]() с целыми
коэффициентами. Ясно, что таких уравнений данной степени
с целыми
коэффициентами. Ясно, что таких уравнений данной степени ![]() счетное множество и
каждое из них имеет конечное множество решений. Значит, по теореме 1 множество
всех алгебраических чисел счетно.
счетное множество и
каждое из них имеет конечное множество решений. Значит, по теореме 1 множество
всех алгебраических чисел счетно.
Следовательно, бесконечные множества:
натуральных чисел ![]() , целых чисел
, целых чисел ![]() , рациональных чисел
, рациональных чисел ![]() и множество всех
алгебраических чисел имеют одинаковую мощность.
и множество всех
алгебраических чисел имеют одинаковую мощность.
Оказывается, не все бесконечные множества
счетны, т.е. эквивалентны множеству ![]() . Такие множества называются несчетными.
. Такие множества называются несчетными.
Г.
Кантор применил новый диагональный метод
и доказал следующее утверждение.
Теорема 2.
Множество действительных чисел из отрезка ![]() несчетно.
несчетно.
Доказательство.
Допустим от противного, что оно счетно. Тогда все
числа из этого отрезка можно последовательно пронумеровать:

Построим
теперь десятичную дробь, которая точно не будет находиться среди этих чисел ![]() Рассмотрим число
Рассмотрим число ![]() , в котором
, в котором ![]() ;
; ![]() … ;
… ;![]() ;… Ясно, что
;… Ясно, что ![]() .
.
Следовательно, множество всех чисел из отрезка ![]() нельзя пронумеровать с
помощью натуральных чисел, оно несчетно.
нельзя пронумеровать с
помощью натуральных чисел, оно несчетно.
В
дополнение к теореме 2 отметим, что
множество чисел из интервала ![]() эквивалентно множеству
всех действительных чисел
эквивалентно множеству
всех действительных чисел ![]() .
.
В самом деле, сопоставим ![]() .
.
Легко
установить также взаимно однозначное соответствие между промежутками: ![]() и
и ![]() ,
, ![]() и
и![]() ,
, ![]() и
и ![]() (при
(при
![]() ).
).
Значит,
любой интервал, невырожденный сегмент или полуинтервал (как множество чисел)
эквивалентен множеству ![]() , а поэтому имеет одинаковую мощность с
, а поэтому имеет одинаковую мощность с
![]() ; эта
мощность называется мощностью континуума.
; эта
мощность называется мощностью континуума.
Г.
Кантор в 1878 году высказал свою знаменитую
континуум-гипотезу: всякое бесконечное подмножество континуума ![]() эквивалентно либо
множеству натуральных чисел
эквивалентно либо
множеству натуральных чисел ![]() , либо всему континууму
, либо всему континууму ![]() .
.
Лишь
десятки лет спустя, известные математики К. Гёдель и П. Коэн доказали, что
вопрос о справедливости континуум-гипотезы
имеет неоднозначный ответ, который зависит от выбора аксиом в качестве системы
аксиом теории множеств.
Напомним,
что действительное (или, вообще, комплексное) число называется трансцендентным,
если оно не является алгебраическим. Как следует из счетности
множества алгебраических чисел и теоремы 2, существует бесконечное (даже
несчетное) множество действительных трансцендентных чисел.
Заметим,
что Г. Кантор доказывает существование трансцендентных чисел, не указывая ни
одного из них. С этим доказательством существования несчетного множества
трансцендентных чисел связаны интересные парадоксы. К примеру, алфавит языка состоит из
конечного числа букв, из различных конечных сочетаний которых составляются
слова. Поэтому по теореме 1 множество фраз, определяемых конечным набором слов,
не более чем счетно. По теореме 2 множество
действительных чисел ![]() несчетно.
Следовательно, остаются действительные числа, которые нельзя определить (или
описать) конечным набором слов, т.е. конечной фразой, какой бы длинной она не
была.
несчетно.
Следовательно, остаются действительные числа, которые нельзя определить (или
описать) конечным набором слов, т.е. конечной фразой, какой бы длинной она не
была.
Значит, само множество всех действительных
чисел содержит противоречие: действительные числа одновременно как отдельные
объекты существуют, но при этом про каждое действительное число отдельной
фразой нельзя сказать, что это такое.
Такой
неожиданный вывод привел к расколу среди широко известных математиков, так как
«существовать» в математике означало «быть свободным от противоречий».
Другой
оригинальный результат также связан с именем Г. Кантора: существуют достаточно редкие (не густые) множества,
которые имеют мощность континуума.
Множество
Кантора показывает, что если в качестве характеристики для сравнения множеств взять их мощность, то получится парадокс: «слишком
разреженное» (нигде не плотное)
множество равно (по мощности) «очень большому» (всюду плотному) множеству
действительных чисел.
Чтобы
построить множество Кантора, отрезок ![]() разбиваем на три
равные части и отбрасываем средний интервал. Каждый из оставшихся двух отрезков
разбиваем на три равные части и отбрасываем их средние интервалы. Затем каждый
из оставшихся четырех отрезков разбиваем
на три равные части и отбрасываем их средние интервалы и т.д.
разбиваем на три
равные части и отбрасываем средний интервал. Каждый из оставшихся двух отрезков
разбиваем на три равные части и отбрасываем их средние интервалы. Затем каждый
из оставшихся четырех отрезков разбиваем
на три равные части и отбрасываем их средние интервалы и т.д.
Множество ![]() , которое остается на отрезке
, которое остается на отрезке ![]() после удаления всех аналогичных
средних интервалов, называется канторовым
совершенным множеством. Оно не содержит изолированных точек, все его точки
суть предельные точки.
после удаления всех аналогичных
средних интервалов, называется канторовым
совершенным множеством. Оно не содержит изолированных точек, все его точки
суть предельные точки.
Покажем, что это канторово множество ![]() эквивалентно всей оси
эквивалентно всей оси ![]() .
.
Для этого числа из отрезка ![]() запишем в виде
троичных дробей:
запишем в виде
троичных дробей: 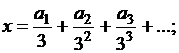
![]() . Ясно, что
. Ясно, что 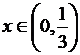 при
при
![]() ;
; 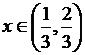 при
при ![]() ;
; 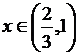 при
при ![]() Концы отбрасываемых
интервалов можно записать двояко:
Концы отбрасываемых
интервалов можно записать двояко: ![]()
![]() (т.е. можно считать
(т.е. можно считать ![]() или
или ![]() ).
).
Аналогично, если число![]() не принадлежит интервалам, отбрасываемым на втором шаге, то
его можно записать в виде троичной дроби с
не принадлежит интервалам, отбрасываемым на втором шаге, то
его можно записать в виде троичной дроби с ![]() . Продолжив анализ троичной записи чисел, получим: канторово
совершенное множество
. Продолжив анализ троичной записи чисел, получим: канторово
совершенное множество ![]() состоит их тех и только
тех чисел
состоит их тех и только
тех чисел ![]() , которые можно записать в троичной форме, используя не более
двух цифр: 0 и 2.
, которые можно записать в троичной форме, используя не более
двух цифр: 0 и 2.
Из множества ![]() выделим подмножество
выделим подмножество ![]() всех чисел,
представимых периодическими троичными дробями, а из отрезка
всех чисел,
представимых периодическими троичными дробями, а из отрезка ![]() - множество
- множество ![]() всех чисел,
представимых периодическими двоичными дробями;
всех чисел,
представимых периодическими двоичными дробями; ![]() в силу их счетности.
в силу их счетности.
Запишем теперь каждое число ![]() из
из
![]() в
виде двоичной дроби и, если
в
виде двоичной дроби и, если  , поставим ему в соответствие такое число
, поставим ему в соответствие такое число 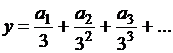 из множества
из множества ![]() , что
, что ![]() оба либо нули, либо
оба либо нули, либо ![]()
![]() .
.
В
результате, с учетом ![]() , получим: достаточно редкое множество
, получим: достаточно редкое множество ![]() (хотя
(хотя ![]() достаточно редкое
множество).
достаточно редкое
множество).
Значит,
мощность множества не в полной мере характеризует это множество. Поэтому наряду
с мощностью для сравнения множеств берутся и другие характеристики: мера Жордана, мера Лебега, емкость множества и др.