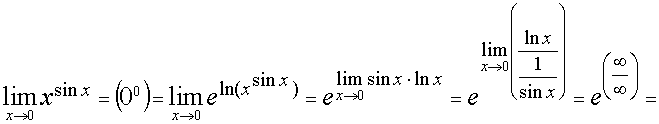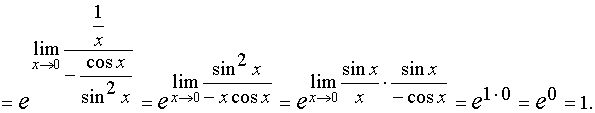Тема 5. СВОЙСТВА ФУНКЦИЙ, НЕПРЕРЫВНЫХ НА ОТРЕЗКЕ
Теорема 1. Если функция f(x) непрерывна на отрезке [a;b], то она достигает на этом отрезке
своих наименьшего m и наибольшего M значений, т.е. для любых x Î [a;b] выполняется неравенство:
m ≤ f(x)
≤ M.
Теорема 2. Если функция f(x) непрерывна на отрезке [a;b], то для любого числа С,
удовлетворяющего неравенству m ≤ С ≤ M, на отрезке [a;b] найдётся хотя бы одна точка х0, в которой выполняется равенство: f(х0)
= С.
Теорема 3. Если функция f(x) непрерывна на отрезке [a;b] и на концах этого отрезка имеет
значения различных знаков, то существует хотя бы одна точка х0 Î (a;b), в которой выполняется равенство: f(х0)
= 0.
5.1. Теорема Ролля
Теорема . Если функция f(x) определена
на отрезке [a;b] и
выполнены следующие условия:
· f(x) непрерывна на отрезке [a;b];
· f(x) дифференцируема на интервале (a;b);
· f(a) = f(b),
то внутри этого отрезка [a;b] найдется хотя бы одна точка х0, в которой
выполняется равенство:
f '(х0)
= 0.
Доказательство. Так как f(x) непрерывна
на отрезке [a;b], то она
достигает на этом отрезке своих наименьшего m и
наибольшего M значений.
Возможны два случая:
m = M и m < M.
· Если m = M, то f(x) = const = m = M. Тогда f '(x) = 0 при любом x Î
[a;b]. Следовательно,
в этом случае теорема верна и при этом в качестве х0 можно рассматривать любое значение x Î
[a;b].
· Если m < M, то исходя из условия f(a) = f(b), по
крайней мере одно из чисел m или M не равно f(a) = f(b). Для определённости предположим, что M – наибольшее значение f(x) достигается не на концах отрезка [a;b], а в некоторой внутренней точке х0 Î (a;b). Тогда в точке х0
для приращения функции справедливо неравенство: Dy = f(х0 + Dx) – f(хо) ≤ 0, так как f(х0)
= M – наибольшее значение f(x) на
отрезке [a;b] и Dx такое, что х0
+ D x Î
[a;b].
· Если D x > 0, то ![]() и существует
и существует ![]()
· Если D x < 0, то ![]() и существует
и существует ![]()
Так как по условию теоремы функция f(x) дифференцируема при xÎ
(a;b), то в
точке хо существует производная. Значит справедливы
равенства:
f ' (х0
+ 0) = f ' (х0 – 0) = f ' (х0) = 0.
Теорема доказана.
Геометрический смысл теоремы Ролля
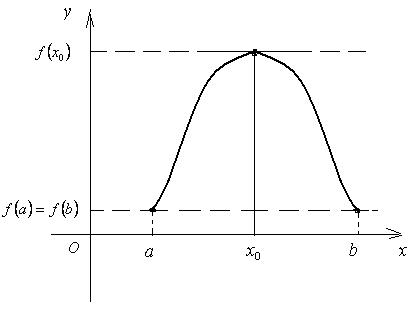
С геометрической точки зрения теорема
Ролля означает, что график функции, непрерывной на отрезке [a;b], дифференцируемой на интервале (a;b) и принимающей на концах отрезка
равные значения, имеет хотя бы одну точку с координатами (х0 ; f (х0)),
где х0Î (a;b), в которой касательная параллельна оси Ox (рис. 7).
5.2. Теорема Лагранжа
Теорема 5 (теорема Лагранжа). Если функция f(x) определена на отрезке [a;b] и выполнены следующие условия:
· f(x) непрерывна на отрезке [a;b],
· f(x) дифференцируема на интервале (a;b),
то внутри этого отрезка существует хотя
бы одна точка х0, в
которой выполняется равенство:
f ' (х0)
= ![]() .
.
Доказательство. Рассмотрим вспомогательную функцию F(x) =
f(x) + l×x, где l = const. Потребуем, что бы для F(x) выполнялось условие F(a) = F(b).
Так как F(a) = f(a) + l×a и F(b) = f(b) + l×b, то получим равенство:
f(a) + l×a =
f(b) + l×b.
Отсюда выразим значение l:
l = – ![]() .
.
При этом значении l
функция F(x) = f(x) – ![]() .
.
Функция F(x) удовлетворяет
всем условиям теоремы Ролля:
· F(x) непрерывна на отрезке [a;b]:
· F(x) дифференцируема на интервале (a;b)
· F(a) = F(b).
Следовательно, по теореме Ролля на интервале (a;b) существует хотя бы одна точка х0, в которой выполняется
равенство:
F '(х0)
= 0.
Найдём F '(x):
F '(x) = f '(x) – 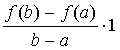 .
.
Поэтому F '(x0) = f '(х0) –![]() = 0, если f '(х0)
=
= 0, если f '(х0)
= ![]() .
.
Теорема доказана.
Геометрический смысл теоремы Лагранжа
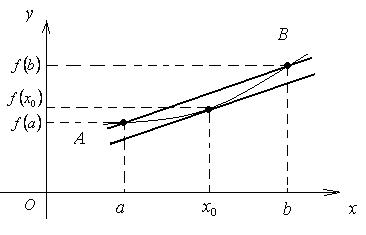
С геометрической точки зрения теорема
Лагранжа означает, что график функции, непрерывной на отрезке [a;b] и дифференцируемой на интервале (a;b), имеет хотя бы одну точку (х0; f(х0),
в которой касательная параллельна секущей, проходящей через точки A(a; f(a)) и B(b; f(b)) (рис. 8)
5.3. Теорема Коши
Теорема. Если функции f(x) и g(x) определены на отрезке [a;b] и удовлетворяют условиям:
· f(x)
и g(x) непрерывны
на отрезке [a;b];
· f(x) и g(x) дифференцируемы на интервале (a;b);
· g '(x) ¹ 0 при любом x Î (a;b),
то внутри отрезка [a;b] найдётся хотя бы одна точка х0, в которой выполняется
равенство:
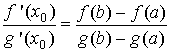 .
.
Доказательство аналогично доказательству теоремы 5 (теорема Лагранжа)
при вспомогательной функции
F(x) = f(x) + l × g(x),
где l = const, которую выбирают так, чтобы F(a) = F(b).
5.4. Правило Лопиталя
Теорема. Если функции f(x) и g(x) определены в некоторой окрестности точки х0 и в этой окрестности они
удовлетворяют условиям:
· f(x) и g(x)
дифференцируемы в каждой точке за исключением может быть самой точки х0;
· g '(x) ¹ 0 для любого x из этой окрестности;
·
![]() или
или ![]() ,
,
тогда, если существует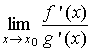 конечный или бесконечный, то выполняется равенство:
конечный или бесконечный, то выполняется равенство:
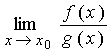 =
= 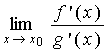 .
.
Замечание 1. Правило Лопиталя используется для раскрытия
неопределённостей типа ![]() или
или ![]() , возникающих при вычислении пределов. Если под знаком
предела оказывается неопределённость другого типа: 0×∞,
, возникающих при вычислении пределов. Если под знаком
предела оказывается неопределённость другого типа: 0×∞,
![]() , 10, 00 или ∞0, то с
помощью тождественных алгебраических преобразований такая неопределённость
приводится к
, 10, 00 или ∞0, то с
помощью тождественных алгебраических преобразований такая неопределённость
приводится к ![]() или
или ![]() и тогда можно
применить правило Лопиталя.
и тогда можно
применить правило Лопиталя.
Замечание 2. Если к условиям теоремы 7 добавить дифференцируемость
функций f '(x) и g'(x) в окрестности точки х0, то при выполнении
остальных требований для f '(x) и g'(x) правило Лопиталя можно применить
повторно. При этом будет справедливо равенство:
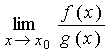 =
= 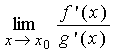 =
= 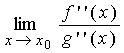
Пример 1. Вычислить предел:
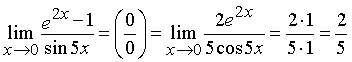
Пример 2.
Вычислить предел:
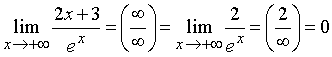
Пример 3.
Вычислить предел:
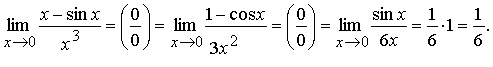
Пример 4. Вычислить предел:
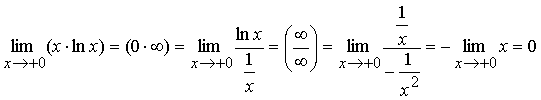 .
.
Пример 5. Вычислить предел:
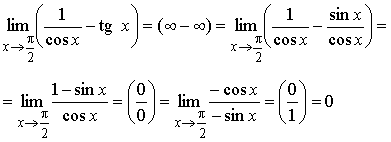
Пример 6. Вычислить предел: