Тема 5. Производная и
дифференциал
4.1. Определение производной, ее геометрический и
механический смысл
4.2. Примеры вывода производных некоторых элементарных
функций
4.3. Таблица производных основных элементарных функций
4.5. Правила дифференцирования
4.6.Дифференцирование функции, заданной неявно
4.7. Производные показательной и степенной функций
4.8. Производные обратных тригонометрических функций
4.1. Определение производной, её геометрический и
механический смысл
Пусть
дана функция ![]() , определённая на множестве D(f). Рассмотрим точку xÎD(f) и некоторое число Dx – такое,
чтобы точка x+DxÎD(f). Это число Dx называется приращением аргумента x.
, определённая на множестве D(f). Рассмотрим точку xÎD(f) и некоторое число Dx – такое,
чтобы точка x+DxÎD(f). Это число Dx называется приращением аргумента x.
Определение 1.
Приращением функции ![]() называется
разность f(x+Dx) – f(x). Приращение функции
называется
разность f(x+Dx) – f(x). Приращение функции ![]() обозначают Dy, т.е. Dy = f(x+Dx) – f(x).
обозначают Dy, т.е. Dy = f(x+Dx) – f(x).
Определение 2. Производной
функции ![]() называется предел
отношения приращения функции Dy к приращению аргумента Dx, если приращение аргумента Dx стремится к нулю и этот предел
существует. Производную функции
называется предел
отношения приращения функции Dy к приращению аргумента Dx, если приращение аргумента Dx стремится к нулю и этот предел
существует. Производную функции ![]() обозначают:
обозначают: ![]() или
или ![]() . Поэтому можно записать:
. Поэтому можно записать:
![]()
Пример. Исходя из определения найти производную функции у =![]() .
.
Решение.
Dy= f(x+ Dx) – f(x) = =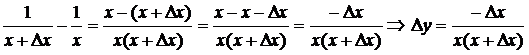 .
.
 .
.
Ответ: 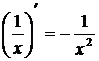 .
.![]()
Механический смысл производной
Пусть материальная точка движется по прямой по закону S =
S(t),
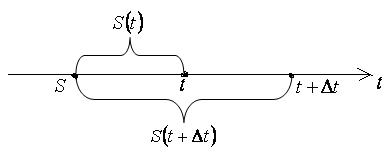
тогда DS = S(t+Dt) – S(t) –
расстояние, пройденное за время Dt и средняя
скорость движения:
![]() .
.
Чтобы
найти скорость движения в момент времени t, надо
рассмотреть предел ![]() при Dt ® 0:
при Dt ® 0:
V(t) = ![]() .
.
Следовательно,
производная от пути S(t) равна
мгновенной скорости точки в момент времени t :
![]() .
.
Геометрический смысл производной
Рассмотрим
график функции y =
f(x) в
окрестности фиксированной точки М0 (рис.
5).
Точка
M0(x0;y(x0)) – фиксированная точка графика ![]() . Точка M(x0+Dx; y(x0+Dx)) при
различных значениях Dx – любая точка на графике. Если точка M приближается к точке M0 (при этом Dx ® 0), то секущая
линия M0M стремится к
своему предельному положению, называемому касательной
к линии y = f(x) в точке M0.
. Точка M(x0+Dx; y(x0+Dx)) при
различных значениях Dx – любая точка на графике. Если точка M приближается к точке M0 (при этом Dx ® 0), то секущая
линия M0M стремится к
своему предельному положению, называемому касательной
к линии y = f(x) в точке M0.

Рис. 5
Рассмотрим треугольник
M0MA: tg j = 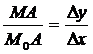 , j –
угол наклона секущей M0 M к оси Ox.
, j –
угол наклона секущей M0 M к оси Ox.
Перейдем к пределу при Dx ®0:
 j =
j = ![]() ,
,
где![]() – угол наклона касательной к оси Ox.
– угол наклона касательной к оси Ox.
Таким
образом, y' (x0) = tg![]() частное значение производной функции
частное значение производной функции ![]() в точке x0 равно угловому коэффициенту касательной, проведённой
к линии y =
f(x) в точке M0(x0; y(x0)). Тогда,
используя уравнение прямой, проходящей через заданную точку M0(x0;y0) с известным угловым коэффициентом Kкас = y'(x0), можно записать уравнение касательной к линии y =
f(x) в точке M0(x0; f(x0)):
в точке x0 равно угловому коэффициенту касательной, проведённой
к линии y =
f(x) в точке M0(x0; y(x0)). Тогда,
используя уравнение прямой, проходящей через заданную точку M0(x0;y0) с известным угловым коэффициентом Kкас = y'(x0), можно записать уравнение касательной к линии y =
f(x) в точке M0(x0; f(x0)):
y = f(x0) + f ' (x0) × (x – x0).
Аналогично,
можно записать уравнение нормали –
прямой, перпендикулярной касательной и проходящей через точку касания M0(x0;f(x0)):
y = f(x0) –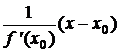 ,
,
используя условие перпендикулярности прямых: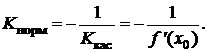
4.2.
Примеры вывода производных некоторых элементарных функций
1) ![]()
Вывод: ![]() ;
; ![]()
![]()
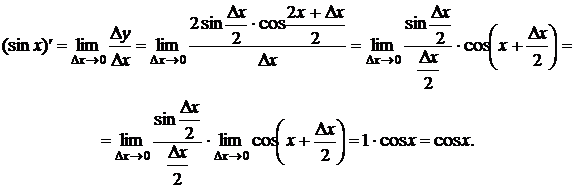
2) ![]() ;
;
Вывод: ![]() ;
; ![]()

3) ![]()
Вывод: ![]() ;
; 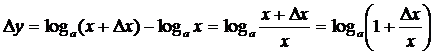
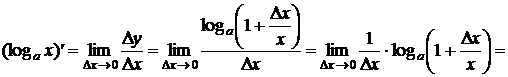

(используется второй замечательный предел и свойства
логарифма).
4) ![]()
Вывод: так как ln x = log e x, то,
используя производную, для (log a x), можно записать:
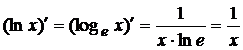 .
.
5) (c)' = 0
Вывод: y =
c, Dy = y(x+Dx) – y(x) = c – c = 0 ![]() .
.
Для остальных
функций производные выводятся позже с помощью правил дифференцирования.
4.3. Таблица производных
основных элементарных функций
1. (c)' = 0
2. (xa)' = a×xa – 1
3.
(ax)'
= ax×ln a, (a >
4. (ex)' = ex
5. (loga x)' = 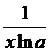 , (a > 0; a ≠ 1)
, (a > 0; a ≠ 1)
6.
(ln x)' =
![]()
7.
(sin x)' =cos x
8.
(cos x)' = – sin x
9.
(tg x)' = ![]()
10.
(ctg x)' = – ![]()
11.
(arcsin x)' = ![]()
12.
(arccos x)' = –![]()
13.
(arctg x)' = 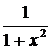
14.
(arcctg x)' = ![]()
4.4. Дифференцируемость
функции. Связь дифференцируемости с существованием производной и непрерывностью
функции
Определение 3. Функция y = f(x) называется
дифференцируемой в точке xÎD(f), если она определена в некоторой
окрестности точки x и её приращение в этой точке можно представить в виде:
Dx = A×Dx + ![]() (Dx)×Dx,
(Dx)×Dx,
где A = A(x) – не
зависит от Dx; ![]() (Dx) – бесконечно малая величина при Dx®0, т.е.
(Dx) – бесконечно малая величина при Dx®0, т.е. ![]()
Теорема 1 (связь дифференцируемости с существованием производной). Функция y = f(x) дифференцируема в точке xÎD(f) тогда и только тогда, когда она
имеет в этой точке производную f '(x). При этом f '(x) = A.
Доказательство.
1) Необходимость: Дано: y =
f(x) дифференцируема в точке х.
Доказать: A = f '(x).
Так
как функция y =
f(x)
дифференцируема в точке х,
то по определению Dy = A × Dx + ![]() (Dx) × Dx, где
(Dx) × Dx, где ![]() (Dx) ® 0 при Dx ® 0.
(Dx) ® 0 при Dx ® 0.
Разделим это
равенство на Dx ≠ 0: ![]()
![]()
Перейдём к
пределу при Dx ® 0:
![]() существует, а значит f '(x) = A.
существует, а значит f '(x) = A.
Необходимость
доказана.
2) Достаточность:
Пусть f ' (x) – существует. Нужно доказать, что f(x)
дифференцируема.
Так
как существует f '(x)=![]() , то по свойству предела можно записать:
, то по свойству предела можно записать: ![]() , где
, где ![]() (Dx) ® 0 при D x® 0.
(Dx) ® 0 при D x® 0.
Умножим это
равенство на Dx:
![]() Þ функция y = f(x),
дифференцируема в точке х.
Þ функция y = f(x),
дифференцируема в точке х.
Достаточность
доказана.
Теорема 2 (связь дифференцируемости с непрерывностью функции). Если функция y = f(x) дифференцируема в точке xÎD(f), то она непрерывна в этой точке.
Доказательство. Так как функция дифференцируема в точке x, то её приращение в этой точке можно представить в
виде:
Dy =
A × Dx +
![]() (Dx) × Dx,
(Dx) × Dx,
где A = f '(x) и ![]() (Dx) ® 0 при Dx ® 0.
(Dx) ® 0 при Dx ® 0.
Найдём предел от Dy при Dx ® 0:
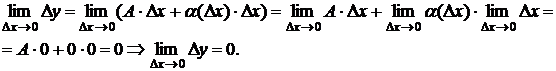
Отсюда
следует, что по определению 2 непрерывности функции в точке функция y = f(x) непрерывна в точке x.
Замечание.
Обратное теореме 2 утверждение не всегда верно.
4.5. Правила
дифференцирования
Теорема 3. Если функции
U(x) и V(x) дифференцируемы в точке x, то функция U(x) ± V(x) дифференцируема в точке x и её
производная вычисляется по формуле:
(U(x)
± V(x))' =
(U(x))' ± (V(x))'.
Доказательство: Рассмотрим функцию y = U(x) ± V(x).
Тогда
Dy = DU ± DV. Разделим на Dx и перейдём к пределу при Dx ® 0:
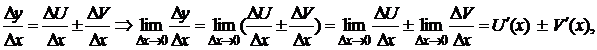
так как по условию теоремы функции U(x) и V(x) дифференцируемы.
Значит,
(U(x) ± V(x))' = U '(x) ± V '(x).
Теорема
доказана.
Теорема 4. Если функции U(x) и V(x) дифференцируемы в точке х, то функция (U(x)×V(x)) дифференцируема в точке х и её
производная вычисляется по формуле:
(U(x)
× V(x))' = (U(x))'× V(x) + U(x) × (V(x))'.
Доказательство.
Рассмотрим функцию ![]() . Найдём её приращение
. Найдём её приращение
Dy =
(U+DU)(V+DV)
– U×V = U×V + U×DV + V×DU + DU×DV – U×V=
= U×DV + V×DU + DU×DV.
Разделим
Dy на Dx и перейдем
к пределу при Dx ® 0:

![]()
так как по условию функции U(x) и V(x) дифференцируемы, а значит ![]() ,
, 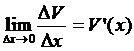 и
и ![]() .
.
Следовательно,
(U(x)× V(x))' = U ' (x) × V(x) + U(x) × V ' (x).
Теорема
доказана.
Следствия:
а) Если U(x), V(x) и W(x) дифференцируемы
в точке х,
то функция (U(x)×V(x) ×W(x)) дифференцируема в точке х и её
производная вычисляется по формуле:
(U×V×W)' = U '×V×W + U×V '×W + U×V×W '.
б)
Производная постоянной, умноженной
на дифференцируемую функцию, равна этой постоянной, умноженной на
производную функции: (C×U(x))' = C×U ' (x).
Теорема 5. Если функции U(x) и V(x) дифференцируемы в точке х и V(x) ≠ 0,
то функция ![]() дифференцируема в
точке х и
её производная вычисляется по формуле:
дифференцируема в
точке х и
её производная вычисляется по формуле:
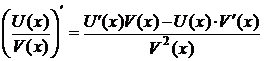 .
.
Доказательство.
Рассмотрим функцию 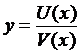 . Найдём её приращение
. Найдём её приращение 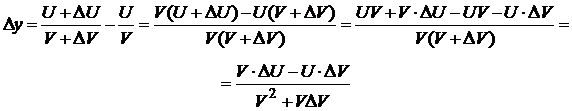
Разделим Dy на Dx и перейдём к пределу при Dx ® 0:
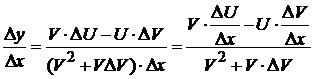 ,
,
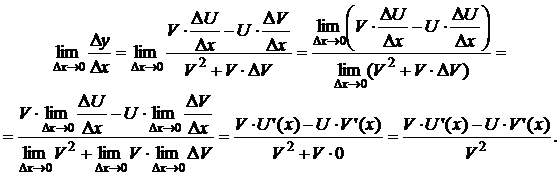
Значит,
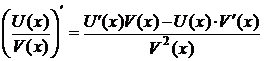 .
.
Теорема
доказана.
Теорема (производная сложной функции). Если функция f(u) дифференцируема в точке u, а функция u(x)
дифференцируема в точке x, причём u = u(x), тогда
сложная функция f(u(x)) дифференцируема в точке x и её производная вычисляется по
формуле:
(f (u(x)))'
= f '(u) ×u' (x).
Доказательство.
Рассмотрим функцию y =
f(u). Так как
функция f(u)
дифференцируема в точке u, то её приращение можно записать в
виде:
![]() ,
,
где ![]() .
.
Разделим на Dx и перейдём к пределу при Dx ® 0:
![]()
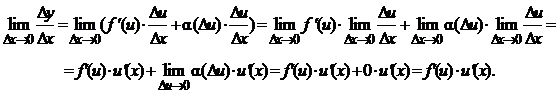
Если D x® 0, то D u® 0, так как u(x) дифференцируема, а значит непрерывна, т.е.
(f(u(x)))' = f ' (u) ×u' (x).
Теорема
доказана.
4.6. Дифференцирование
функции, заданной неявно
Пусть функция ![]() задана неявно
уравнением
задана неявно
уравнением ![]() . Дифференцируя это равенство по x по правилу
дифференцирования сложной функции, находим из полученного равенства y'.
. Дифференцируя это равенство по x по правилу
дифференцирования сложной функции, находим из полученного равенства y'.
Пример. Найти y', если функция y задана
уравнением:
x3 + y3 – xy = 0
Решение.
3x2 + 3y2×y’ – y – xy’ = 0
y’(3y2 – x) = y – 3x2
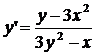
Ответ: 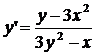 .
.
4.7. Производные
показательной и степенной функций
Теорема 1. Степенная
функция y = xa (aÎR) дифференцируема при любом
xÎR и справедлива формула:
(xa)' = a ×xa – 1.
Доказательство.
Прологарифмируем равенство y = xa, предполагая x > 0: ln y = a× ln x
Получили
уравнение от x и y, задающее
функцию y = xa неявно. Найдём производные от обеих
частей равенства:
![]()
Выразим отсюда y': ![]() .
.
Подставим в
полученное равенство y = xa:
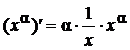 ,
, ![]() .
.
Теорема
доказана.
Теорема 2. Показательная функция y = ax
(a >
(ax)'
= ax × ln a
Доказательство. Прологарифмируем равенство y = ax:
ln y = x ln a.
Получили
уравнение от x и y, задающее
функцию y =
ax неявно. Найдём производные от обеих частей
равенства:

Выразим
отсюда y':
y' = y × ln a.
Подставим
в полученное равенство y =
ax :
(ax)' = ax × ln a.
Теорема
доказана.
Замечание. В
частном случае, при a = e полученная формула в теореме 8
принимает вид:
(ex)' = ex × ln e или (ex)' = ex.
Теорема 3. Если функции U(x) и V(x) дифференцируемы в точке x, то
показательно-степенная функция y = (U(x))V(x)
дифференцируема в точке x и справедлива формула:
![]() .
.
Доказательство можно выполнить с
помощью логарифмирования равенства y = (U(x))V(x)
по основанию логарифма e и дальнейшего дифференцирования
обеих частей полученного равенства.
4.8. Производные обратных
тригонометрических функций
Теорема 1. Функция y = arcsin x дифференцируема при любом xÎ(–1;1) и справедлива формула:
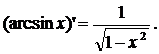
Доказательство:
Функция y =
arcsin x определена
при x Î[–1;1] и область ее значений 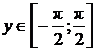 . Она монотонно возрастает на всей области её определения,
поэтому имеет обратную функцию x =
sin y. Уравнение x = sin y можно рассматривать как неявное задание функции y = arcsin x. Найдём производную от обеих частей уравнения:
. Она монотонно возрастает на всей области её определения,
поэтому имеет обратную функцию x =
sin y. Уравнение x = sin y можно рассматривать как неявное задание функции y = arcsin x. Найдём производную от обеих частей уравнения: ![]() .
.
Выразим из
полученного равенства y':
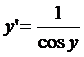 .
.
Но ![]() при
при 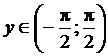 . Поэтому
. Поэтому ![]() , так как
, так как ![]() .
.
Следовательно,
получаем: 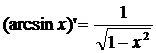 .
.
Теорема 2. Функция y = arсcos x дифференцируема при x Î(–1;1) и справедлива формула: 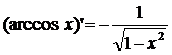 .
.
Теорема 3. Функция y = arctg x дифференцируема при x Î(–¥;+¥) и справедлива формула: 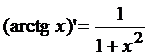 .
.
Теорема 4. Функция y = arcсtg x
дифференцируема при x Î(–¥;+¥) и справедлива формула:  .
.
Теоремы
2, 3, и 4 доказываются аналогично теореме 1.
4.9. Дифференциал функции
Пусть
функция y =
f(x)
дифференцируема в точке x, тогда её приращение можно записать
в виде двух слагаемых, первое из которых линейно относительно Dx, а второе слагаемое – бесконечно
малая величина при Dx ® 0 (более высокого порядка малости по сравнению с Dx):
![]() ,
,
где ![]() (Dx) ® 0 при Dx ® 0.
(Dx) ® 0 при Dx ® 0.
Определение 4. Слагаемое ![]() называется главной линейной относительно Dx частью приращения функции y =
f(x),
называемой дифференциалом этой
функции. Дифференциал обозначается
называется главной линейной относительно Dx частью приращения функции y =
f(x),
называемой дифференциалом этой
функции. Дифференциал обозначается
dy =
y' (x)× Dx .
Если
x – независимая переменная, то справедливо равенство Dx = dx, так как (x)' = 1. Тогда формула для дифференциала
записывается: dy = y' (x)× dx .
Так
как второе слагаемое приращения функция – малая величина более высокого порядка
малости по сравнению с Dx, то между приращением функции и её
дифференциалом можно приближённо поставить знак равенства. Это равенство тем
точнее, чем меньше Dx. На основе этого приближённого равенства получается
приближённое представление значения дифференцируемой функции:
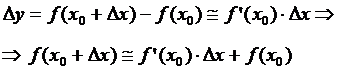
Пример. Вычислить приближённо ![]()
Решение. Рассмотрим функцию ![]() . В качестве начальной точки возьмём x0 = 4, приращение Dx = 0,08,
. В качестве начальной точки возьмём x0 = 4, приращение Dx = 0,08, ![]() и подставим в формулу:
и подставим в формулу:
![]() ,
,
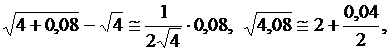
![]() , где D
<< 0,08.
, где D
<< 0,08.
Геометрический смысл дифференциала
Рассмотрим график дифференцируемой функции y = f(x) в некоторой окрестности точки x0 (рис. 6):
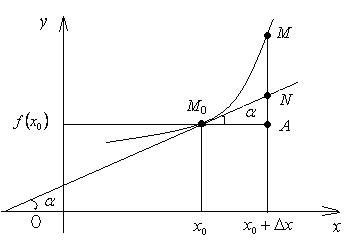
Из DM0AN
AN = M0A×tg a =
Dx×f '(x0) = dy.
Итак: дифференциал функции y =
f(x) в точке x0 равен
приращению ординаты касательной (AN), проведённой к кривой y = f(x) в точке (x0; f(x0)), при переходе от x0 к x0+Dx (от точки М0 в точку М).
Инвариантность формы дифференциала
Теорема. Пусть функция
y =
f(u)
дифференцируема в точке u, а функция u = u(x)
дифференцируема в соответствующей точке x (u =
u(x)). Тогда
для сложной функции y =
f(u(x)) справедливо равенство: dy = f '(u)du = y'(x)dx.
Доказательство.
Сложная функция y=f(u(x)) является дифференцируемой в точке x. Поэтому справедливо равенство:
dy = y'(x)dx .
Но так как
функция y(x) = f(u(x)) сложная,
то
y' (x) = f ' (u) × u' (x).
Поэтому dy = y'(x)dx =
f '(u)×u'(x)dx = f '(u)×du, так как по условию теоремы функция u = u(x)
дифференцируема в точке x, следовательно, du = u' (x)×dx.
Теорема
доказана.