Тема
1. Множества. Элементарные функции. Действительные числа
1.1. Множества и действия над ними
1.3. Определение
функции одной переменной
1.5. Сложная и
обратная функции
1.1. Множества и действия над ними
В математике первичными понятиями являются понятия множества и элемента множества. Множества обозначают большими латинскими
буквами A, B, ..., а их элементы – малыми a, b, ... Если элемент a принадлежит множеству A, то пишут aÎA. В противном случае пишут aÏA.
Множество, не содержащее ни одного элемента, называется пустым и обозначается Æ.
Множество A называется подмножеством
множества B, если любой элемент множества A является элементом множества B. Пишут AÌB или BÉA и говорят, что множество A включено во множество B или B включает A.
Множества A и B называются равными, если они
состоят из одних и тех же элементов. Записывают это так: A=B.
Включение AÌB не исключает равенства этих множеств. Если же AÌB, но A¹B и A¹Æ, то A называют собственным подмножеством
множества B.
Если множество A включено во множество B или совпадает с ним, то пишут AÍB или BÊA.
Множество называется конечным,
если оно содержит конечное число элементов. Множество, не являющееся конечным, называется
бесконечным.
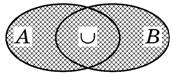Если заданы два множества A и B, то через AÈB обозначается множество, называемое их
объединением или суммой и состоящее из всех тех элементов, каждый из которых
принадлежит хотя бы одному из множеств A и B. Таким образом, если некоторый элемент принадлежит множеству AÈB, то он принадлежит либо только множеству A, либо только множеству B, либо обоим этим множествам одновременно.
Для любого множества A (непустого или пустого) полагается AÈÆ=A.
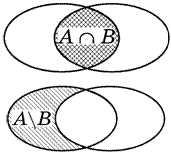
Через A∩B обозначается множество, состоящее из
всех элементов, которые одновременно принадлежат как множеству A, так и множеству B. Множество A∩B называется пересечением множеств A и B. Если A и B не имеют общих элементов (в
частности, одно из них или оба пусты), то полагают A∩B=Æ. В этом случае множества A и B называются непересекающимися.
Отметим, что пустое множество
совпадает само с собой: Æ=Æ, но вместе с тем оно не пересекается само с собой: Æ∩Æ=Æ.
Через 
обозначается множество, называемое разностью
множеств A и B и состоящее из всех элементов, которые принадлежат множеству A, но не принадлежат множеству B. Говорят также, что получается из
множества A вычитанием из него множества B.
Если BÌA, то разность называется дополнением множества B до множества A. По определению, полагается 
.
Введём ряд нужных в дальнейшем понятий и изучим некоторые
свойства числовых множеств.
Если для подмножества X действительных чисел существует
такое число b, что оно не меньше каждого числа xÎX, т. е. для любого xÎX выполняется неравенство x£b, то множество X называется ограниченным сверху,
а число b – числом,
ограничивающим сверху множество X.
С помощью логических символов определение ограниченного
сверху множества записывается в виде: X ограничено сверху Û $bΡ "xÎX: x£b;
отсюда X не ограничено сверху Û "bΡ $xÎX: x>b, т. е. множество X не ограничено сверху, если, каково бы ни было число bΡ, найдётся такое число xÎX, что x>b.
Множество, не являющееся ограниченным сверху множеством,
называется неограниченным сверху
множеством.
Заметим, что если число b ограничивает сверху множество X, то любое число, большее b, также ограничивает сверху множество X.
Если $bÎX "xÎX: x£b, то число b называется наибольшим или
максимальным числом множества X.
Очевидно, что, если во множестве X имеется наибольшее число, то оно единственно, а само множество X в этом случае ограничено сверху этим числом.
Аналогично множеству, ограниченному сверху, определяется
множество, ограниченное снизу.
Если для подмножества X действительных чисел существует
такое число a, что оно не больше каждого числа xÎX, т. е. для любого xÎX выполняется неравенство a£x, то множество X называется ограниченным снизу,
а число a – числом, ограничивающим снизу это множество.
Множество, не являющееся ограниченным снизу множеством, называется
неограниченным снизу множеством.
С помощью логических символов определение ограниченного снизу
множества записывается в виде: X ограничено снизу Û $aΡ "xÎX: x³a; отсюда
X не ограничено снизу Û "aΡ $xÎX: x<a, т. е. множество X не ограничено снизу, если, каково бы ни было число aΡ, найдётся такой элемент xÎX, что x<a.
Очевидно, что если число a ограничивает снизу множество X, то и любое число a'<a также ограничивает снизу это множество.
Если $aÎX "xÎX: a£x, то число a называется наименьшим или
минимальным числом множества X.
Если во множестве X имеется наименьшее число, то оно
единственно, а само множество X в этом случае ограничено снизу этим числом.
Множество, ограниченное и сверху и снизу, называется ограниченным множеством.
Другими словами, множество XÌ¡ называется ограниченным, если существуют такие числа a и b, что для любого xÎX выполняется неравенство a£x£b.
Множество, не являющееся ограниченным, называется неограниченным. Очевидно, что
неограниченное множество может быть неограниченным и сверху и снизу или только
сверху или снизу.
1.2. Грани числовых множеств
Рассмотрим произвольное множество XÌ¡.
Наименьшее среди всех чисел, ограничивающих сверху множество XÌ¡, называется его верхней гранью
и обозначается sup X (от лат. supremum
наибольший).
Наибольшее среди всех чисел, ограничивающих снизу множество XÌ¡, называется его нижней гранью
и обозначается inf X (от лат. infimum
наименьший).
Иногда верхнюю (нижнюю) грань множества называют точной верхней (нижней) гранью этого множества.
Если во множестве существует наибольшее (наименьшее) число,
то оно является верхней (нижней) гранью этого множества. В частности, такая
ситуация имеет место для конечных множеств: любое конечное множество чисел
имеет наибольшее и наименьшее числа, а потому нижнюю и верхнюю грани.
Выясним теперь вопрос: всегда ли у числового множества
существует его верхняя (нижняя) грань? Если множество ограничено сверху
(снизу), то ответ дается следующей теоремой.
Теорема. Всякое ограниченное сверху непустое
числовое множество имеет верхнюю грань, а всякое ограниченное снизу непустое
числовое множество имеет нижнюю грань.
Если множество не ограничено сверху (снизу), то, как уже
отмечалось, никакое число не может являться его верхней (нижней) гранью, так
как вообще нет чисел, которые его ограничивают сверху (снизу). Для удобства
вводится следующее определение.
Верхней гранью неограниченного сверху числового множества
называется +¥, а нижней гранью неограниченного
снизу числового множества называется –¥.
Удобство этого определения состоит в том, что теперь каждое
непустое числовое множество имеет верхнюю (нижнюю) грань, принадлежащую
расширенному множеству действительных чисел.
1.3. Определение функции одной
переменной
Определение.
Пусть даны два множества X и Y. Если каждому элементу x из множества X по некоторому правилу f соответствует
единственный элемент y
из множества Y, то говорят, что на
множестве X определена функция y = f(x) с областью определения X =
D(f) и областью изменения Y = E(f). При этом x считают независимой переменной, или аргументом функции, а y – зависимой переменной или функцией.
Частным значением функции y = f(x) при
фиксированном значении аргумента x = x0 называют y0 = f(x0).
Графиком функции y = f(x) называют геометрическое место точек
M(x;f(x)) на плоскости
Oxy, где x Î D(f) и
f(x) Î E(f).
1.4.
Способы задания функции
1) Аналитический способ –
способ задания функции с помощью формулы.
Различают несколько способов
аналитического задания функции:
а) Функция задана явно формулой y = f(x).
Например: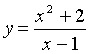 
,
где D(y) = (– ∞;1)
(1;+∞).
б) Функция задана неявно уравнением, связывающем
x и y: F(x;y) = 0.
Например: 
– уравнение окружности
с центром в начале координат и радиусом r. Если из этого уравнения выразить y через x, то получится две функции:
и 
,
которые имеют область определения 
, а области значений этих функций будут: для первой – 
, для второй – 
.
в) Функция задана параметрически с помощью
некоторого параметра t,
причём и аргумент x,
и функция y
зависят от этого параметра:
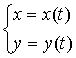
Например: можно задать окружность 
с помощью
параметрических уравнений:
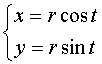
2) Табличный способ задания функции – например, таблицы Брадиса задают функции y = sin x, y = cos x и др.
3) Графический способ задания функции, когда зависимость функции от её
аргумента задаётся графически.
1.5.
Сложная и обратная функции
Определение 1. Пусть
функция y = f(U) определена на множестве D(f), а функция U = g(x) определена на D(g), причём E(g)
D(f).
Тогда функция y = F(x) = f(g(x)) называется сложной
функцией (или функцией от функции, или суперпозицией
функций f и
g ).
Определение 2. Пусть задана
функция y = f(x) взаимно однозначно
отображающая множество X = D(f) на
множество Y = E(f). Тогда
функция x =
g(y) называется
обратной к функции y = f(x), т. е. любому y
E(f) соответствует
единственное значение xD(f), при
котором верно равенство y =
f(x).
Замечание. Графики функций y = f(x) и x = g(y) представляют одну и ту же
кривую. Если же у обратной функции независимую переменную обозначить x, а зависимую y, то графики функций y = f(x) и y = g(x) будут симметричны относительно биссектрисы первого и
третьего координатных углов.
1.6.
Элементарные функции
Основные элементарные функции:
y =
const (постоянная
функция), D(y) = R; E(y) = c.
(линейная функция), D(y) = R; E(y) = R.
y =
(степенная функция), α ÎR, E(y), D(y) зависят от
α.
y =
(показательная функция), a >
y =
(логарифмическая функция) ), a >
Тригонометрические функции:
y =
sin x, D(y) = R, E(y) =
.
y = cos x, D(y)
= R, E(y) =.
y = tg x, D(y) = 
, E(y) = R.
y = ctg x, D(y) = 
, E(y) = R.
Обратные тригонометрические функции:
y = arcsin x, D(y)
= , E(y) = 
.
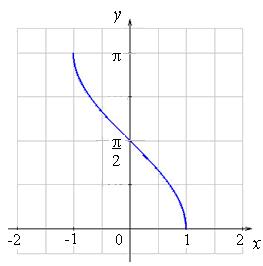
y = arccos x, D(y)
= , E(y) = 
.
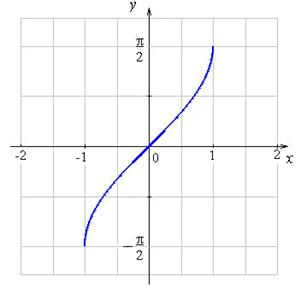
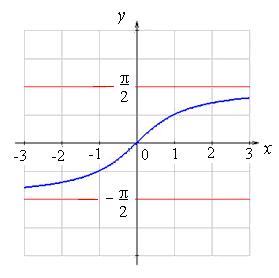
y = arctg x, D(y)
= R, E(y) = 
.
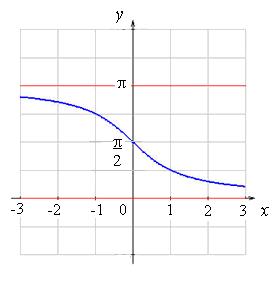
y = arcctg x, D(y)
= R, E(y) = 
.
Элементарной функцией называется функция, составленная из основных элементарных функций с
помощью конечного числа операций сложения, вычитания, умножения, деления и
суперпозиции.
Например: 
– элементарная функция.
Графики обратных тригонометрических функций:
|
y = arcsin x
|
y = arccos
x
|
|
y = arctg x
|
y = arcctg x
|
1.7.
Действительные числа
Множеством натуральных чисел называются числа, используемые при счете и обозначается 
. Множество всех натуральных чисел, ноль и числа, противоположные
натуральным, образуют множество целых чисел: 
.
Рациональным
числом называют число, представимое в виде отношения некоторого целого
числа к некоторому натуральному числу. Множество всех рациональных чисел
обозначается через 
. Следовательно,
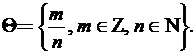
Хотя
рациональных чисел бесконечно много, их не хватает для измерения длин,
площадей, объемов и т.д.
Измерить длину
отрезка означает сравнить его с другим отрезком. Оказывается, если взять два
произвольных отрезка с длинами 
и 
, то не всегда с помощью одного можно найти длину другого,
если ограничиться только множеством рациональных чисел. Таковыми являются,
например, сторона и диагональ квадрата. Если взять в качестве масштабной
единицы какой-нибудь отрезок, сторону и диагональ нельзя выразить с помощью
рациональных чисел. Следовательно, для измерения величин (длины, площади т.д.)
нужно расширить множество рациональных чисел.
Заметим, что
любое рациональное число можно представить в виде некоторой бесконечной
периодической десятичной дроби. Для этого достаточно числитель разделить на
знаменатель в столбик.
Аналогично
каждую бесконечную десятичную дробь можно обратить в обыкновенную дробь.
Поэтому рациональное число можно определить следующим образом: рациональным
числом называется бесконечная периодическая десятичная дробь, взятая со
знаком «+» или «-».
Легко привести
примеры десятичных дробей, которые не являются периодическими. Таковой
является, например, дробь 0,1010010001… Число 1 не является периодом, так как как угодно далеко в записи этой
дроби встречаются нули. Аналогично ноль не является периодом. Следовательно,
существуют непериодические десятичные дроби, они называются иррациональными
числами. Множество иррациональных чисел обозначается 
. Оказывается, если объединить все периодические и
непериодические десятичные дроби, то задача измерения величин полностью
решается.
Множество всех
рациональных и иррациональных чисел образует множество действительных чисел.
Обозначается 
.