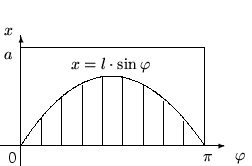Предлагаемое читателю учебное пособие посвящено изложению основ одной из современных областей математической науки – теории вероятностей. Она написана на основе многолетнего опыта авторов по чтению лекций, проведению семинарских занятий, а также организации самостоятельной работы студентов по университетскому курсу «Теория вероятностей и математическая статистика».

На естественных факультетах университета при изложении материала авторы старались, не снижая математической строгости, максимально удовлетворить современным требованиям его прикладной направленности. С этой целью вместе с введением новых вероятностных понятий, формул исчисления вероятностей и законов распределения случайных величин определяются также области их приложений, физические и производственные процессы, описываемые этими распределениями. Этому способствует также, и то, что в книгу включен параграф §12, содержащий основные способы моделирования случайных величин с заданными законами распределения. Этот важный вопрос получения множества независимых значений некоторой случайной величины до сих пор остается вне учебной программы, хотя с этой проблемой приходится встречаться при решении как вероятностных, так и статистических задач. В этом же параграфе в качестве практического применения законов больших чисел и центральной предельной теоремы излагаются основы одного из современных универсальных численных методов – метода статистических испытаний или, как его часто называют, метода Монте-Карло; приводятся некоторые примеры его применения.

Книга содержит 12 параграфов, каждый из которых состоит из трех частей: теоретической, решения нескольких типовых задач и задач и упражнений по теме для самостоятельной работы студентов.

Согласно учебным планам предмет теории вероятностей и математической статистики читается на старших курсах вузов. Предполагается, что к этому времени слушатели знакомы с основными математическими понятиями, необходимыми для современного изложения теории, опирающейся на основания теории множеств и теории меры. Однако, книга содержит краткие сведения по всем необходимым понятиям для того, чтобы материал был доступен также для студентов не математиков (§§1-8).

§ 1. ЭЛЕМЕНТЫ ТЕОРИИ МНОЖЕСТВ И КОМБИНАТОРИКИ

Классическое определение понятия вероятность связано с опытами с равновозможными исходами. При этом вероятность некоторого события , связанного с рассматриваемым опытом, определяется как отношение числа благоприятствующих этому событию исходов опыта (то есть исходов, при которых событие происходит) к числу всех возможных исходов:

В конкретных случаях подсчет чисел и представляет собой довольно трудную задачу. Часто этому помогают комбинаторные методы.

События рассматриваются обычно, как некоторые подмножества множества возможных исходов опыта. Комбинаторика изучает способы подсчета числа элементов в различных множествах, состоящих из конечного числа элементов.

1.1. Множества

Под множеством мы будем понимать совокупность некоторых элементов, имеющих какую – то определенную природу, общность или какой-то общий признак. Множество будем обозначать большими буквами латинского или русского алфавита, а элементы множества соответствующими маленькими буквами с индексами: А-множество, элемент этого множества,

Пример 1. Множество исходов эксперимента, состоящего в подбрасывании монеты 1 раз: ={Г, Р}, где Г –«герб», Р - «решка».

Пример 2. Множество исходов опыта, состоящего в подбрасывании игральной кости:

Пример 3. Множество цифр: = {0,1,2,3,…,9}.

Принадлежность элемента а множеству пишется: ; элемент а не принадлежит . Множество из одного элемента называется элементарным: Пустое множество обозначается символом .

Множества и равны (), если каждый элемент множества принадлежит множеству и наоборот.

Например, множество решений квадратного уравнения и множество {1,2} равны.

Обозначение – множества и не равны.

Для отношения равенства между множествами вводятся так же, как и для чисел, понятия рефлексивность, симметричность и транзитивность:

1) ,

2) если , то ,

3) если А=В и В=С, то А=С,

Объединением двух множеств и называется такое множество , элементы которого принадлежат хотя бы одному из этих множеств.

Пример 4. ={1,3,5,...} - множество всех нечетных натуральных чисел, ={2,4,6,...} - множество всех четных натуральных чисел. Тогда объединением и будет множество всех натуральных чисел:

Пересечением множеств и называется такое множество элементы которого принадлежат каждому из этих множеств.

Например, для множеств из предыдущего примера выполняются равенств:

Говорят, что множества и не пересекаются, если

Множество называется частью множества , если каждый элемент множества принадлежит . Обозначение: . Чаще говорят, что множество является подмножеством множества .

Пустое множество является частью любого множества.

Если и , то будем говорить, что множество В строго содержится в множестве : .

Например, , .

Дополнением части множества до множества называется множество , состоящее из всех элементов множества , не принадлежащих множеству .

Пример 5:

Часто мы имеем дело с подмножествами , , ,... одного и того же множества . Если рассматриваются дополнения до этого множества, то вместо «дополнение множества до множества » будем говорить просто «дополнение » а вместо ( ) -писать .

Свойства дополнений. Пусть произвольное множество, и - некоторые его части. , - дополнения и . Тогда:

5) .

Свойства 1)-3) достаточно просты и вытекают из определений объединения, пересечения и дополнения. Однако, их можно доказать и более строго. Для того, чтобы указать путь доказательства этих свойств, а также аналогичных задач об эквивалентности (равенстве) двух множеств, докажем свойство 4). Пусть - некоторый элемент множества принадлежит множеству Тогда по определению дополнения Значит и , , то есть и а это означает, что

Таким образом, мы показали, что . Покажем теперь обратное включение.

Пусть Тогда и т. е. и . Значит, или . Итак, Если и , то множества и равны. Свойство 4) доказано.

1.2. Элементы комбинаторики

Напомним, что комбинаторика занимается способами подсчета числа элементов различных конечных множеств. Число элементов некоторого множества обозначим через

Правило сложения. Если множества и не пересекаются, т.е. то

Пример 6. Пусть ={1,3,5}, ={2,4,6}. Тогда

Пример 7. ={1,2,3,5}, ={2,4,6}.

Используя принцип индукции, нетрудно получить аналогичное правило для конечного числа n попарно непересекающихся множеств:

Правило умножения. Пусть и произвольные множества. Декартовым произведением этих множеств будем называть множество упорядоченных пар , где

Пример 8. =={1,2.3,4,5,6}, ={11,12,...,16,21,...,66} - множество всевозможных исходов, связанных с бросанием двух игральных костей.

Пример 9. = = {0.1.2,...,9} - множество цифр.

Тогда ={00,01,...,99} - множество всех двузначных чисел.

Число элементов декартова произведения конечных множеств и равно произведению чисел и элементов этих множеств:

Правило умножения для произведения конечного числа множеств:

Пример 10. Число всевозможных двоичных чисел длины 10 (т.е. последовательностей из десяти нулей и единиц) будет равно:

Перестановки. Перестановками из элементов называются взаимно однозначные отображения множества из элементов на себя. Число всех перестановок из элементов равно:

Пример 11. Сколькими способами можно рассадить 5 гостей за стол на 5 стульях с номерами от 1 до 5? Всего таких способов

Выборки. Пусть задано множество с элементами которое назовем генеральной совокупностью.

Выборкой объема из генеральной совокупности называется упорядоченная последовательность , где - некоторое подмножество индексов из множества .

Эту последовательность можно образовать следующим образом выбираем из всей генеральной совокупности, - из генеральной совокупности без элемента и т.д. Такая выборка называется выборкой без возвращения. Ясно, что должно быть

Поставим вопрос: сколько выборок объема без возвращения можно произвести из генеральной совокупности из элементов?

Рассуждаем следующим образом: на первом месте может стоять любой из элементов, элемент можно выбрать способами и т.д., последним -ым элементом выборки может быть любой из оставшихся элементов.

Таким образом, используя правило умножения комбинаторики, находим, что искомое число совпадает с числом размещений из по :

Пример 12. Сколькими способами можно выбрать 2 из 10 членов борцовской команды и выставить против 2-х борцов из команды противника?

Если выборку организовать таким образом, что каждый раз выбранный элемент после его фиксации возвращать обратно в генеральную совокупность, то такая выборка называется выборкой с возвращением. Рассуждая так же, как и выше, получим, что число таких выборок равно .

Выборки без возвращения объема из генеральной совокупности из элементов, отличающиеся только составом, называются сочетаниями из элементов по и обозначаются

Число выборок без возвращения объема , имеющих одинаковый состав и отличающихся только порядком, будет .

Поэтому, число выборок, различающихся только составом, будет в раз меньше, чем размещений :

Для сочетаний верны следующие соотношения:

Пример 13. Пусть в урне находятся , шаров, из которых черных, – белых шаров. Сколько выборок объема , отличающихся составом, можно составить? Сколько таких выборок, содержащих ровно черных шаров, можно составить?

Ответ на первый вопрос - способами. Чтобы ответить на второй вопрос, рассуждаем следующим образом: черных шаров из имеющихся черных можно выбрать способами. Тогда оставшиеся белых шаров можно выбрать из белых шаров cпособами.

Таким образом, число выборок объема , отличающихся составом и содержащих ровно черных шаров будет (в соответствии с правилом умножения)

Упражнения к параграфу.

1. Доказать, что

Решение. Пусть - произвольный элемент, . Если , то , если же и то и в этом случае тоже Таким образом,

(*)

Покажем теперь, что имеет место и обратное включение.

Пусть . Тогда или . В первом из этих случаев имеем, что . Если же , то и , и в этом случае тоже , т.е.

(**)

Соотношения (*) и (**) доказывают искомое тождество.

2. Доказать, что

Решение. Известно правило сложения: если , то . Представим множество как объединение двух непересекающих множеств

По правилу сложения

откуда следует доказательство.

3. Сколькими способами можно рассадить за стол гостей на стульях с номерами 1,…, , если для двоих гостей места вполне определены?

Решение. Если места для двух гостей уже определены за столом, то остаются места для гостей. Таким образом, задача сводится к расстановке гостей по местам: число способов будет .

4. Сколькими способами можно образовать сборную команду в 10 человек из команд и двух городов, если классных игроков в них n(A)=12 и n(B)=8, а количество делегируемых игроков пропорционально этим числам?

Решение. В соответствии со сказанным из города должно быть делегировано

игроков, а из города - 4 игрока.

Множество способов выбора 6 игроков из 12 содержит элементов, т. е. Аналогично, 4 игрока из команды В можно выбрать множеством способов с количеством элементов

По правилу умножения искомое число способов скомпонования сборной команды

5. Сколькими способами можно вычеркнуть 6 номеров из 49 в игре "Спортлото"?

6. Сколькими способами можно рассадить за круглый стол человек так, чтобы два определенных лица оказались рядом?

7. Из двух ящиков, содержащих соответственно -белых, - черных и - белых, - черных шаров, вытаскивают по одному шару. Сколько всего различных способов вытащить при атом шары разных цветов?

8. Сколько двузначных чисел можно составить из цифр 0.1,2,,...,9? Сколько четных двузначных чисел можно составить?

9. Из колоды в 52 карты выбирают 3 карты. Сколько существуют комбинаций, когда среди этих 3 карт окажется ровно один туз?

10. Сколькими способами можно рассадить 6 пассажиров по 10 вагонам?

11. Некто не знает шифра кнопочного замка автомобиля, состоящего из 9 кнопок. Известно, что шифр состоит из набора цифр 0,1,2,...,9. Сколько вариантов в максимуме придется ему перепробовать, чтобы завести машину?

12. Тот же вопрос, но замок состоит из 6 барабанов, на каждом из которых имеются цифры от 0 до 9.

13. Из группы 20 студентов отбирается 5 человек для контрольной проверки знаний. Причем, по согласованию с комиссией одного представителя отбирают из числа 4 отличников и 1 - из состава 3 явных двоечников. Сколькими способами можно выбрать этих 5 человек?

14. Сколько различных билетов с указанием станций отправления и назначения нужно отпечатать, если всего на железной дороге 25 станции?

15. Из учащихся 4-х классов составляют команду из 6 человек для участия в районной математической олимпиаде. Сколькими способами это можно сделать, если в команду должны входить представители всех классов, а число "математиков" в них равно соответственно 10, 11, 12 и 13?

16. Сколькими способами можно раздать колоду в 36 карт между 4-мя игроками?

17. Сколько различных подмножеств можно образовать из множества А = включая и пустое подмножество?

Воспользоваться формулой Ньютона

и вытекающей из нее для любого натурального n формулой

18. Пусть имеется различных пар, каждая из которых состоит из одинаковых элементов. Сколькими способами из них можно выбрать 2 элемента?

19. Монету бросают 10 раз подряд. Сколько при этом возможны различные последовательности из букв «Р» (решка) и «Г» (герб) длины 10?

20. В условиях задачи 19 сколько таких последовательностей, в которых буква "Р" встречается ровно 3 раза?

21. (модель Максвелла-Больцмана). Рассмотрим распределение n частиц, отмеченных номерами 1,..., по областям фазового пространства (). Вообще-то, в каждой области может находиться любое количество этих частиц. Однако, будем считать, что состояние рассматриваемой системы определяется числами частиц в 1-ой,..., -ой областях фазового пространства. Описанная модель называется моделью Максвелла-Больцмана.

Сколько существует распределений частиц по областям, приводящих систему в состояние

22. Сколько всего существуют различных распределений частиц по областям пространства в модели Максвелла-Больцмана?

23. (Модель Бозе-Эйнштейна). В статистике Бозе-Эйнштейна важно только сколько частиц попало в область, но не индивидуальность попавших частиц. Сколько существует всевозможных размещений частиц по областям пространства в этой модели?

24. (Модель Ферми-Дирака). Согласно этой статистике в ячейке может находиться либо одна частица, либо не находиться ни одной; индивидуальности частиц также нет. Вопрос: Сколько существует различных размещений частиц по областям пространства в модели Ферми-Дирака?

25. Сколькими способами можно распределить три билета среди 20 студентов, если: а) распределяются билеты в разные театры, а каждый студент может получить не более одного билета; б) распределяются билеты в разные театры и на разные дни, а каждый студент может получить любое (не превышающее трех) число билетов; в) распределяются равноценные билеты на вечер и каждый студент может получить не более одного билета?

26. В студенческой группе 24 человека. Необходимо избрать старосту и профорга. Сколькими способами можно образовать эту руководящую двойку, если одно лицо может занимать только один пост?

27. Сколькими способами можно расположить на шахматной доске 8 ладей так, чтобы они не могли бить друг друга.

28. Сколько разных трехзначных чисел можно составить из цифр 1, 2, 3, 4 и 5 при условии, что а) ни одна цифра не повторяется, б) цифры могут повторяться?

29. На тренировках занимаются 12 баскетболистов. Сколько может быть образовано тренером разных стартовых пятерок?

30. Первый курс факультета должен представить на студенческую конференцию 10 делегатов. Сколькими способами может быть выбрана эта десятка, если на курсе учатся 70 человек?

31. Сколько различных «слов», состоящих из трех букв, можно образовать из букв слова СТАТИСТИКА? А если «слова» состоят не менее чем из трех букв?

32. Сколькими способами можно выбрать один цветок из корзины, в которой имеется 12 гвоздик, 15 роз и 7 хризантем?

33. Группа студентов изучает 10 различных дисциплин. Сколькими способами можно составить расписание занятий в понедельник, если в этот день должно быть 4 разных занятия?

34. Сколько разных пятизначных чисел можно составить из цифр 1, 2, 3, 4 и 5 при условии, что ни одна цифра не повторяется?

35. В урне 12 белых и 8 черных шаров. Сколькими способами можно выбрать 5 шаров, чтобы среди них было: а) 5 черных; б) 3 белых и 2 черных?

36 Игральная кость (на ее 6 гранях нанесены цифры от 1 до 6) бросается 3 раза. Сколько существует вариантов выпадения очков в данном опыте? Напишите некоторые из них.

37. Сколькими способами можно распределить 6 различных подарков между четырьмя ребятишками?

Контрольные вопросы

1. Что изучает комбинаторика?

2. Что определяет правило сложения и правило умножения?

3. Какая выборка называется выборкой с возвращением и выборкой без возвращения? Приведите примеры.

4. В чем отличие размещений и сочетаний?

5. Для решения каких задач используют перестановки?

§ 2. СОБЫТИЯ И ОПЕРАЦИИ НАД НИМИ

Исходным понятием теории вероятностей является понятие пространства элементарных событий - это множество всех мыслимых исходов некоторого эксперимента. Оно будет обозначено символом , а элемент этого множества (элементарное событие) символом .

Выделение пространства элементарных событий представляет собой первый шаг в построении вероятностной модели того или иного эксперимента.

Рассмотрим несколько примеров.

1. При однократном бросании монеты пространство состоит из двух точек:

={Г,Р},

где Г - выпадение "герба", Р - выпадение "решки".

2. При -кратном бросании монеты

и общее число элементарных событий

В этих примерах пространство элементарных событий было конечным множеством. Можно привести многочисленные примеры экспериментов, имеющих бесконечное число возможных исходов.

3. Монету бросают до первого появления герба

означает, что герб появится при -ом бросании монеты.

4. Задача о встрече. Два лица условились встретиться в интервале времени . Если через обозначим время прихода первого лица, а через - второго, то пространство

т.е. в этом случае представляет собой множество точек квадрата со сторонами, равными .

5. Наблюдается частица, совершающая броуновское движение.

Пространство элементарных событий - множество всех возможных траекторий частицы.

2.1.Случайные события - подмножества пространства

Обычно интересуются не тем, какой конкретно исход имеет место в результате испытания, а тем принадлежит ли исход тому или иному подмножеству всех исходов. Таким образом, с каждым пространством элементарных событий связывают некоторое множество его подмножеств, называемых событиями и обозначаемых обычно большими латинскими буквами ,.... Точки из называют элементарными событиями, благоприятствующими событию .

Примеры событий:

Пример 1. Пусть монету бросают дважды и - событие, состоящее в том, что хотя бы один раз появится «герб». Тогда = {ГГ, ГР, РГ, РР}, ={ГГ, ГР, РГ}.

Событие – «монета выпадет одной и той же стороной»:

={ГГ, РР}.

Пример 2. В задаче о бросании монеты до первого появления герба пусть - событие, состоящее в том, что будет сделано не больше трех бросании, - «будет сделано четное число бросаний»:

Пример 3. В задаче о встрече предположим, что каждое лицо ждет второго не больше 20 минут и событие – «встреча состоится». Тогда .

Введем теперь отношение порядка и алгебраические операции над событиями. Эти операции являются, по существу, операциями над множествами и отличаются только терминологией.

1. Само множество называют достоверным событием, так как никакие другие исходы эксперимента, кроме тех, которые описываются точками , по определению невозможны.

2. Пустое множество (множество, не содержащее ни одной точки ) отождествляют с событием, которое не может происходить в данном эксперименте. Его называют невозможным событием и обозначают символом .

3. События частично упорядочены: обозначает, что если событие происходит, то событие В также происходит. В этом случае говорят, что из события следует, событие {событие влечет за собой событие ). Очевидно, для любого : .

4. Если то говорят, что и эквивалентны, и пишут .

5. Каждому событию можно поставить в соответствие другое событие называемое противоположным . Событие происходит тогда и только тогда, когда не происходит.

6. Суммой (объединением) событий и назовем событие, обозначаемое или , которое происходит, тогда и только тогда, когда происходит или или , или оба вместе. Аналогичный смысл имеет сумма любого числа событий: - событие, состоящее в том, что произойдет хотя бы одно из событий

Заметим, что для любого события

,, +=, .

7. Произведением (пересечением) события и назовем событие, обозначаемое или , которое происходит, тогда и только тогда, когда происходят и вместе, одновременно. Отметим очевидные соотношения:

Два события и называются несовместимыми, если их совместное (одновременное) появление невозможно: .

8. Разность двух событий и (обозначается ) есть событие, происходящее тогда и только тогда когда происходит , но не происходит .

Очевидно .

Пример 4. Бросается игральная кость, пусть выпадение четного числа очков, В выпадение числа очков, не больше 3:

где - выпадение очков при бросании кости, .

Тогда событие означает, что выпадет число очков, отличное от пяти,

«выпадет число очков, равное двум»;

А-В = { -«выпадет число очков, равное 4 или 6»;

«выпадет нечетное число очков».

Пример 5. На квадрат случайно бросается точка (см. рис.1). Обозначим через - точка падает в малый круг. В - точка падает в большой круг. Тогда события А+В, АВ, , означают попадание точки в соответствующие заштрихованные области.

Рис.1. Геометрическая интерпретация действий над событиями.

В более общем случае бесконечного пространства элементарных событий рассматривают не все события, а лишь некоторые классы этих событий, называемые алгеброй и - алгеброй событий.

Определение. Класс F подмножеств пространства называется алгеброй событий, если выполнятся следующие условия:

1) F;

2) из F следует, чтоF ;

3) из F следует, что F.

Определение. Алгебра событий называется -алгеброй, если из F, следует, что

Нетрудно показать, что, если F , то , тоже принадлежат F; невозможное событие F

В заключении приведем таблицу соответствия понятий теории множеств и теории вероятностей.

Обозначение

Терминология

Теории множеств

Терминология

Теории вероятностей

Универсальное множество

Пространство элементарных событий, достоверное событие

Элемент множества ;

некоторое множество элементов

Элементарное событие ;

событие

объединение множеств и

пересечение множеств и

сумма событий и ;

произведение событий

или )

пустое множество

дополнение

невозможное событие;

противоположное событие

и не пересекаются

подмножество

и несовместимы событие влечет за собой событие

А-В

Разность множеств и

Разность событий и

Упражнения к параграфу.

1. Из урны, содержащей черные и белые шары извлечены шаров. Пусть - событие, состоящее в том. что -ый извлеченный шар белый. Выразить через следующие события:

а) все извлеченные шары белые,

б) хотя бы один шар будет белым,

в) ровно один шар будет белым,

г) не более шаров белые,

д) все шаров одного цвета.

2. Доказать равенства:

3. Мишень состоит из 10 кругов, ограниченных концентрическими окружностями с радиусами причем Событие - попадание в круг радиуса .

Что означают события:

4. Производится стрельба по цели до первого попадания. Описать множество элементарных событий и записать следующие события:

а) стрельба закончится до 5-го выстрела.

б) потребуется четное число выстрелов.

5. Электрическая цепь составлена по схеме, приведенной на рис.2. Обозначим - выход из строя -го элемента (=1,2.3,4,5). Запишите и , если - событие, состоящее в том, что произойдет разрыв цепи.

Рис.2.

6. Пусть и - события. Найдите все события такие, что:

а) АХ = АВ,

б)

7. Пусть и - подмножества плоскости определены следующим образом:

Изобразите события

8. Пусть : описать события .

9. Пусть. Представить в виде объединения несовместимых событии.

10. Доказать: (А+В)-В = А-АВ = = А-В,

АС-В = АС-ВС,

(А-В)+(А-С) = А-ВС.

11. На отрезке наудачу ставятся две точки, пусть , - координаты этих точек. Изобразить на плоскости области, соответствующие событиям , , , , , , где – «вторая точка блике к левому концу отрезка, чем первая точка к правому концу», – «расстояние между точками меньше половины длины отрезка».

12. Двое играют в шахматы. Событие означает, что выиграл первый игрок, событие В - что выиграл второй. Что означают события: , ,

13. Двое стрелков поочередно стреляют по цели. Стрельба заканчивается при поражении цели кем-либо из игроков или после расхода всех патронов. Описать события и , состоящие в прекращении стрельбы каждым из игроков, если они имели по 2 патрона.

14. Пусть A, B и C - три произвольных события. Найти выражения для событий, состоящих в том, что а) произошло только событие A; б) произошли A и B, C не произошло; в) все три события произошли; г) произошло по крайней мере одно из событий; д) произошло одно и только одно событие.

15. В цепь включены пять элементов, как показано на рисунке, каждый из которых может отказать во время работы. Рассматриваются события А_i, заключающиеся в том, что i-й элемент отказал. Записать событие A ={цепь не работает}.

16. В ящике лежит большое количество ключей, среди которых находится нужный. Рассматриваются события A_i={Нужный ключ обнаружился при i-й попытке}. Записать событие B={Для поиска нужного ключа понадобилось не более трех попыток}.

17. Известно, что события A и B произошли, а событие C не произошло. Произошли или не произошли следующие события: A + BC; (A + B)C; AB + C; ABC?

18. Пусть - все исходы некоторого эксперимента. События , , . Записать событие .

19. Пусть А и В – произвольные случайные события. Упростить случайное событие .

20. Упростить выражение .

Контрольные вопросы

1. Какое явление можно назвать случайным событием, элементарным исходом?

2. Какие виды случайных событий существуют?

3. Как определить пространство элементарных событий?

4. Что называется алгеброй событий?

5. Приведите соответствия понятий теории и теории вероятностей.

§ 3. ВЕРОЯТНОСТЬ

Сравнивая между собой случайные события, мы часто говорим, что одно из них более вероятно, чем другое. Например, при извлечении шара из урны, содержащей 5 белых и 20 черных шаров, более вероятно появление черного шара (событие ), чем появление белого.

Чтобы придать подобным сравнениям точный количественный смысл, необходимо с каждым событием связать число, характеризующее меру (степень) объективной возможности его наступления. Это число называется вероятностью и обозначается символом (читается: вероятность события ).

Рассмотрим случайный эксперимент с конечным или счетным числом возможных исходов - элементарных событий:

Пусть каждому поставлено в соответствие число , называемое вероятностью элементарного события и все обладают следующими свойствами:

1) ,

2) .

Определение. Вероятностью события называется сумма вероятностей элементарных событий, составляющих данное событие

. (3.1)

Введенная таким образом вероятность события обладает следующими очевидными свойствами:

1. Вероятность любого события заключена между нулем и единицей

(3.2)

2. Вероятность достоверного события равна единице

. (3.3)

3. Если и несовместимые события (Ø), то

. (3.4)

Некоторые следствия:

1. Вероятность невозможного события равна нулю

Ø. (3.5)

Доказательство очевидно.

2. Вероятность противоположного события равна

. (3.6)

Доказательство следует из соотношений , Ø и свойств вероятности.

3. Теорема сложения. Вероятность суммы двух произвольных событий равна

. (3.7)

Доказательство. Представим и в виде сумм несовместимых событий:

и .

По свойству 3

и .

Из этих равенств следует (3.7).

3а. . Это следует из теоремы сложения (3.7) и в силу неотрицательности .

4. Если , то

. (3.8)

Доказательство очевидно.

Определение. Говорят, что для данного эксперимента построена вероятностная модель , если: во-первых, указано пространство элементарных событий и, во-вторых, каждому приписана вероятность , причем и . Вероятность же произвольного события, наблюдаемого в данном эксперименте, определяется по формуле (3.1).

Рассмотрим примеры:

1. Построим вероятностную модель эксперимента, состоящего в двухкратном бросании симметричной монеты:

Так как монета симметрична, то все элементарные события считаем одинаково возможными и каждому из них припишем вероятность .

Рассмотрим, например, событие - хотя бы один раз выпадет «герб»:

Тогда

2. Пусть симметричная монета бросается до тех пор пока не выпадет «герб». Тогда

, где .

Припишем вероятность . Очевидно

Подсчитаем вероятность события - «будет произведено нечетное число бросаний»: ;

3. Эксперимент состоит в однократном бросании правильной игральной кости, Необходимо найти вероятность события состоящего в выпадении четного числа очков (событие ) или числа очков равного 5 (событие ).

Решение.

Понятно, что и Ø, т.е. и несовместимые события.

Тогда

4. Пусть теперь бросают 2 правильные игральные кости, а событие состоит в выпадении четного числа очков или 5 на какой – либо из них. Найти вероятность события .

Решение.

Пусть событие состоит в выпадении четного числа очков или 5 на 1-ой кости, событие - на 2-ой кости.

Использование формулы (3.4) приводит нас к величине, большей 1. Дело в том, что события и совместимые. Поэтому здесь надо воспользоваться формулой (3.7).

3.1. Классическое определение вероятности

Ответ на вопрос о том, как задавать вероятности элементарных событий , является трудным и лежит вне рамок теории вероятностей. Однако имеется много примеров конечных пространств элементарных событий, в которых из соображений симметрии все мыслимые исходы эксперимента можно считать равновозможными (равновероятными). В таких случаях говорят о классическом определении вероятности (определение, с которого развивалась теория вероятностей).

Пусть содержит конечное число элементарных событий , причем все они равновероятны: , .

Определение. Если событию благоприятствуют элементарных событий, т. е. (), то вероятность этого события

. (3.9)

Для решения задач на классическое определение применяются комбинаторные методы.

К таким задачам относятся, в частности, задачи, связанные с урновой схемой.

Пример. Из колоды карт (36 карт) наудачу вынимаются 6 карт. Найти вероятность того, что среди них окажется один туз.

Решение. Всевозможные случаи (исходы) отбора 6 карт (общее число всех элементарных событий) из 36 - это число сочетаний из 36 по 6, т.е. . Один туз можно отобрать из 4 тузов способами, а остальные 5 карт в наборе должны быть не тузами, что можно образовать способами. Наборов, где один туз и пять не тузов, по правилу умножения в комбинаторике будет . Тогда искомая вероятность

3.2.Частотное определение вероятности

Частота случайного события. Рассмотрим некоторый случайный эксперимент и событие , наблюдаемое в этом эксперименте. Повторим испытание раз. При этом пусть событие появилось раз. Отношение называется частотой события в проведенной серии испытаний.

Частота обладает следующими очевидными свойствами:

1. ;

2. ;

3. Если и два несовместимых события, то

Частота вычисляется после проведения испытаний и она изменяется от одной серии испытаний к другой. Однако в больших сериях испытаний частота сохраняет почти постоянное значение. Из приведенной ниже таблицы видно, что при бросании симметричной монеты частота выпадения "герба" колеблется около числа 0.5, причем с увеличением числа испытаний отклонение частоты от числа 0.5 становится все меньше и меньше:

экспериментатор	число бросаний	число выпадений «герба»	частота
Ж.Бюффон	4040	2048	0.5080
К.Пирсон	12000	6019	0.5016
К.Пирсон	24000	12012	0.5005

Из сказанного следует частотное определение вероятности: если при больших частота события колеблется около некоторого числа , то говорят, что событие статистически устойчиво, а число принимается за вероятность события .

Приведенное определение, очевидно, не является строго математическим и математическая теория вероятностей не строится, исходя из этого определения. Тем не менее оно играет важную роль для приложений: истолкование вероятностных расчетов дается через данное частотное определение. Так, если известна вероятность некоторого события , то можно утверждать, что при большом числе испытаний число наступлений этого события будет приблизительно равно .

Частотное определение вероятности события характеризует естественно-научное содержание понятия вероятности и не может служить ее формальным определением. Формальное определение дается при аксиоматическом построении теории вероятностей.

3.3. Геометрическая вероятность

Недостаточность классического определения вероятности (см. формулу (3.9)) очевидна: оно применимо к конечным множествам равновозможных элементарных событий. Рассмотрим здесь некоторое видоизменение этого определения, относящееся к бесконечным множествам и называемое геометрической вероятностью.

Формулу (3.9) классической вероятности можно обобщить на случай непрерывных множеств элементарных событий.

Пусть - некоторая квадрируемая область на плоскости и в ней содержится другая область с квадрируемой границей. В область наудачу бросается точка. Спрашивается, чему равна вероятность попадания этой точки в область ? При этом считается, что вероятность попадания точки в любую подобласть пропорциональна площади этой области и не зависит от ее расположения и формы. Тогда вероятность попадания точки в область равна

, (3.10)

где, и - площади областей и соответственно. Формула (3.10) обобщается на случай пространства любой размерности. В зависимости от размерности может быть длиной, площадью, объемом и т.д.

Задача Бюффона. Плоскость разграфлена параллельными прямыми, отстоящими друг от друга на расстоянии . На плоскость бросают иглу длиной (). Найти вероятность того, что игла пересечет какую-нибудь прямую.

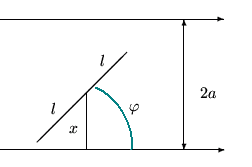
Решение. Пусть - расстояние от центра иглы до ближайшей прямой (рис.3), а - угол, составленный иглой с этой прямой. Величины и полностью определяют положение иглы. Следовательно, .

Рис. 3.

Игла пересечет прямую (событие ) тогда и только тогда, когда выполнено условие и . Искомая вероятность равна отношению площади, заштрихованной на рис.3 области (область ) к площади прямоугольника :

. (3.11)

Формулу (3.11) можно использовать для экспериментального определения числа . Предположим, что игла брошена на плоскость раз, и пусть - число пересечений. При достаточно большом числе испытаний в соответствии с пунктом 3.2 частота события должна быть близка к вероятности , т.е. должно выполняться соотношение

, откуда имеем .

Таких экспериментов для определения числа было проведено много:

экспериментатор, год	число бросаний	число пересечений	значение
Вольф, 1850	5000	2532	3.1596
Смит, 1855	3204	1218	3.1553
Лаззерини, 1901	3408	1808	3.145929

3.4. Аксиомы теории вероятностей

Аксиоматическое построение теории вероятностей было дано впервые А.Н.Колмогоровым в 1933 г. и состоит в установлении связи теории вероятностей с метрической теорией функций и теорией множеств.

С каждым опытом свяжем некоторое конечное или счетное множество так называемых элементарных событий , , определяемых следующим образом: 1) в результате осуществления опыта наступает одно и только одно из событий ; 2) любое событие , связанное с опытом , представляет собой сумму некоторого множества элементарных событий.

Таким образом событие будем отождествлять с множеством элементарных событий , при которых это событие наступает, и будем писать .

Через F - обозначим множество всех подмножеств . Для множества F будем предполагать, что выполняются следующие условия:

1). F и ØF, где Ø - пустое множество (невозможное событие), - достоверное событие;

2) из F следует, что F ( - противоположное событие);

3) из того, что F и F следует, что F и F;

4) из F, при , следует, что F и F.

Следовательно, F является - алгеброй случайных событий (или соответствующих им множеств). Введем теперь аксиомы, определяющие вероятность.

A1. Каждому случайному событию из F поставлено в соответствие неотрицательное число , называемое его вероятностью: .

A2. .

А3. (аксиома аддитивности). Если Ø при любых , , т.е. события попарно несовместимы, то

Нетрудно показать, что все свойства вероятности, приведенные выше, вытекают из этих аксиом. Введем также еще одну аксиому, называемую аксиомой счетной аддитивности или расширенной аксиомой сложения.

А4. Если событие равносильно наступлению хотя бы одного из попарно несовместимых событий ., то

Расширенная аксиома сложения эквивалентна следующей аксиоме непрерывности: Если последовательность событий такова, что каждое последующее влечет за собой предыдущее (т.е. ) и произведение всех событий есть невозможное событие, то

при .

Множество называется пространством элементарных событий; F- -алгеброй случайных событий или соответствующих подмножеств множества ; - вероятность (мера), определенная на -алгебре F.

Тройка F называется вероятностным пространством.

Таким образом, введенные Колмогоровым аксиомы позволяют строить теорию вероятностей, как часть общей теории меры, а вероятность рассматривать как неотрицательную нормированную аддитивную функцию множества.

Используя сформулированные аксиомы, можно установить все полученные в § 3 свойства вероятности. Сформулируем их в виде теорем:

Теорема 1. Вероятность события , противоположного событию , равна :

. (3.12)

Доказательство следует из равенств , Ø и аксиом А2, А3.

Следствие. Вероятность невозможного события Ø равна 0:

Ø. (3.13)

В равенстве (3.12) положим , Ø.

Теорема 2. Пусть и - случайные события, такие, что ( влечет ). Тогда

. (3.14)

Доказательство. Т.к. , то , причем события и несовместимые. Поэтому по аксиоме А3 имеем

откуда и следует равенство (3.14).

Следствие. Если , то .

Теорема 3. Если и - произвольные случайные события, то

. (3.15)

Эту теорему называют теоремой сложения вероятностей.

Доказательство. Событие можно представить в виде суммы трех попарно несовместимых событий:

(см. рис.4)

Рис. 4.

По аксиоме сложения А3 и теореме 2

Обобщая формулу (3.15) для любого числа событий, получим следующую теорему сложения.

Теорема 4. Вероятность наступления хотя бы одного из событий ,т. е. определяется формулой:

. (3.16)

Доказательство проводится методом индукции (предоставляется студентам).

В качестве иллюстрации формулы (3.16) рассмотрим следующий пример.

Задача о совпадениях. На отдельных карточках написаны числа . Карточки располагаются в случайном порядке. Какова вероятность того, что хотя бы одна из карточек окажется на месте с таким же номером?

Решение.

Введем следующие события: - хотя бы одна из карточек окажется на месте с таким же номером, - карточка с номером окажется на месте с номером , .

Очевидно, . Имеем:

......

По формуле (3.16) получим:

Упражнения к параграфу.

1. В урне белых и черных шаров. По схеме случайного выбора с возвращением извлекаются шаров. Найти вероятности следующих событий:

;

2. Наудачу выбирается пятизначное число. Найти вероятности следующих событий:

;

3. За круглым столом в случайном порядке садятся 5 мужчин и 5 женщин. Найти вероятности того, что два лица одинакового пола не окажутся рядом.

4. Колода из 36 карт хорошо перемешена. Карты в случайном порядке расположили на столе слева направо. Найти вероятности следующих событий:

;

5. Задача де Мере. Какое событие более вероятно:

или

6. человек, в том числе и становятся в случайном порядке. Найти вероятность того, что между и окажутся человек.

7. В лотерее билетов, среди которых выигрышных. Какова вероятность выигрыша для обладателя билетов?

8. В ящике имеется 100 яиц, из них 5 некачественных. Наудачу вынимают одно яйцо. Найдите вероятность того, что вынутое яйцо некачественное.

9. В урне 30 шаров: 12 белых, 10 красных и 8 синих. Какова вероятность вынуть цветной шар, если вынимается один шар?

10. Из 30 экзаменационных билетов студент может ответить на 24. Какова вероятность его успешного ответа на экзамене на билет при однократном извлечении билета?

11. Найти вероятность того, что в наудачу написанном двузначном числе цифры разные.

12. Набирая номер телефона, абонент забыл 2 последние цифры и набрал их наугад. Найти вероятность того, что набраны нужные цифры.

13. Из цифр 0, 1, 8 составлено четырехзначное число А. Какова вероятность, что А=8888? Какова вероятность, что А содержит хоть одну восьмерку?

14. В три вагона поезда случайным образом садятся 9 пассажиров. Найти вероятности следующих событий:

;

15. Поток из космических частиц регистрируются системой из счетчиков. Каждая частица с одинаковой вероятностью попадает в любой из счетчиков. Какова вероятность того, что наличие частиц будет зарегистрировано счетчиками?

16. Статистика Максвелла-Больцмана: различных частиц размещаются по ячейкам. Найти вероятности следующих событий:

;

Найти вероятность того, что данная ячейка содержит частиц. Для какого значения эта вероятность будет максимальна?

Доказать, что , если и возрастают так, что среднее число частиц на одну ячейку .

17. Статистика Бозе-Эйнштейна: неразличимых частиц распределяются по ячейкам. Решить следующие задачи:

а) Найти вероятности следующих событий:

;

б) Найти вероятность того, что в данной ячейке будет частиц;

в) Доказать, что , когда и возрастают так, что .

г)Доказать, что при , , т.е. нуль - наиболее вероятное число частиц в данной ячейке.

18. Внутри квадрата с вершинами в точках , , , наудачу выбирается точка . Найти вероятность того, что эта точка окажется в круге радиуса 1/2.

19. Шар помещен внутри эллипсоида

Найти вероятность того, что поставленная наугад внутри эллипсоида точка окажется внутри шара.

20. Стержень длины ломается на три части, выбирая наугад места разлома. Найти вероятность того, что из получившихся частей можно составить треугольник.

21. Предполагая, что все значения и являются равновероятными и единственно возможными, определить вероятности событий:

;

22. Из отрезка наудачу взяты два числа. Какова вероятность того, что их сумма больше единицы, а произведение меньше единицы?

23. Слой воздуха толщины содержит пылинки радиуса в количестве штук в одной кубической единице. Найти вероятность того, что луч света, перпендикулярный слою, не пересекает ни одной пылинки.

24. На отрезке длины поставлены наугад две точки и . Какова вероятность того, что точка окажется ближе к точке , чем точка ?

25. Мишень имеет форму окружности радиуса R. Стрелок выбивает 15 очков, если попадает в малый круг в центре с радиусом r, причем r<R. Какова вероятность выбить 15 очков при одном выстреле?

26. На окружности радиуса наугад поставлены три точки , , . Какова вероятность того, что треугольник остроугольный?

27. В любые моменты времени промежутка равновозможны поступления в приемник двух сигналов. Приемник будет забит, если разность между моментами поступления сигналов будет меньше . Определить вероятность того, что приемник будет забит.

28. Пусть и случайные события такие, что . Доказать, что .

29. Описать пространство элементарных событий и множество для опыта, состоящего в однократном подбрасывании 2-х монет.

30. В коробке находятся шары. Из коробки наугад извлекают 5 шаров и 2 из них оказались красными. Найти относительную частоту появления красного шара.

Контрольные вопросы

1. Что называют вероятностью события?

2. В чем сходство и отличие классического, геометрического и статистического определения вероятности?

3. Как находится вероятность суммы, произведения событий? Для каких событий используются специальные формулы?

4. Чему равна вероятность противоположного события?

5. Сформулируйте аксиомы теории вероятностей.

§ 4. Условная вероятность. Независимость событий

При определении вероятности случайного события мы опираемся на вероятностное пространство F, определяемое некоторым опытом, вернее комплексом условий , в которых этот опыт проводится, F. Если при вычислении вероятности ничего, кроме сказанного не подразумевается, то такая вероятность называется безусловной.

В то же время, очень часто приходиться иметь дело со случаями, когда необходимо вычислять вероятность события , при дополнительном (кроме комплекса условий ) условии, что некоторое событие уже произошло.

4.1. Условная вероятность. Теорема умножения вероятностей

Определение. Вероятность события , вычисляемая при условии, что некоторое другое событие произошло, называется условной вероятностью события и обозначается .

Пример 1. Из урны, содержащей 10 белых и 5 черных шаров, извлекают последовательно два шара без возвращения. Пусть - событие «первый шар будет белым» и - «второй шар будет белым». Тогда вероятность события зависит от того, каким был шар, извлеченный первый раз. Если первый раз был извлечен белый шар (произошло событие ), то , если же произошло (первый раз извлечен черный шар), то . Таким образом,

, .

Исходя из классического определения вероятности, для условной вероятности имеет место формула (при условии ):

или , (). (4.1)

Действительно, пусть , . Пусть событию благоприятствуют , событию - , а их произведению - элементарных событий. Если произошло событие , то для события благоприятными будут лишь из элементарных событий, составляющих событие . Тогда

В общем же случае аксиоматики Колмогорова ( - произвольное множество) формула (4.1) принимается за определение условной вероятности.

Определение. Пусть F - вероятностное пространство, , F. Условной вероятностью события F при условии, что произошло , называют

Условная вероятность обладает такими же свойствами, что и безусловная:

1. - это следует из того, что ;

2. и Ø, так как и ØØ;

3. , если ; в частности, ;

4. , если и несовместимые события; тогда и также несовместимы и .

5. Для произвольных событий и

Действительно, из формулы (4.1) и правила сложения вероятностей имеем:

6. - следует из 2), так как .

Пример 2. Рассмотрим семьи, имеющие двух детей. Спрашивается, какова вероятность того, что в семье оба ребенка мальчики при условии, что:

а) старший ребенок - мальчик?

б) по крайней мере один из детей – мальчик?

Решение. Пространство элементарных событий

где означает, что старший ребенок – мальчик, а младший – девочка и т. д. Будем считать, что каждый исход равновозможен:

Обозначим через - событие «старший ребенок - мальчик», - «младший ребенок - мальчик». Тогда есть событие «по крайней мере один из детей мальчик», - «оба ребенка мальчики». Тогда, считая, что вероятности рождения мальчика и девочки одинаковы, получим:

Формулу (4.1) можно записать в следующем виде:

. (4.2)

Соотношение (4.2) называют теоремой умножения вероятностей: вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого при условии, что первое событие наступило.

Методом индукции можно показать, что

Пример 3. Из урны, содержащей 2 белых и 3 черных шара, двое игроков поочередно вытаскивают по одному шару (без возвращения). Выигрывает тот, кто первым вытащит белый шар. Найти вероятность выигрыша для каждого из игроков.

Решение. Введем события: - «выигрывает первый игрок», - «выигрывает 2-ой игрок», - «игрок при -ой попытке вытащил белый шар», - «игрок при –ой попытке вытащил белый шар».

Тогда

, ;

Впрочем, ясно, что , и вероятность события можно было найти из свойства .

4.2. Формула полной вероятности и формула Байеса

Определение. Говорят, что случайные события образуют полную группу событий, если в результате опыта одно из них обязательно произойдет, т. е.

Определение. События называются попарно несовместимыми, если для любых

Ø, .

Теорема 1. Пусть - полная группа попарно несовместимых событий и - событие, связанное с некоторым опытом. Тогда

. (4.3)

Доказательство. Так как образует полную группу попарно несовместимых событий, то событие может произойти только одновременно с одним из них. Поэтому можно записать, что

События попарно несовместимы, так как попарно несовместимы. Таким образом,

Из последнего соотношения и теоремы умножения (4.2) получаем формулу (4.3).

Пример 4. Среди 25 экзаменационных билетов 5 «несчастливых». Студенты подходят за билетами один за другим. У кого больше вероятности взять «несчастливый» билет: у того, кто подошел первым или у того, кто подошел вторым?

Решение. Вероятность взять «несчастливый» билет для первого студента равна 5/25=1/5. Пусть – событие “второй студент взял “несчастливый” билет”. Можно сделать предположения: – первый студент взял «несчастливый» билет, – первый взял «счастливый» билет. Тогда по формуле (4.3) имеем

Итак, второй студент возьмет “несчастливый” билет с той же вероятностью 1/5, что и первый.

Формула (4.3) называется формулой полной вероятности, а события , , …, называются гипотезами.

Теорема 2. Пусть , , …, - образуют полную группу попарно несовместимых событий. Тогда, при условии , имеют место формулы

(4.4)

Формулы (4.4) называют формулами Бейеса.

Доказательство следует из теоремы умножения и формулы (4.3):

откуда имеем

Схема применения формул (4.4) при решении практических задач следующая. Пусть событие может наступить с одним из событий , причем вероятности известны до опыта, известны также условные вероятности . Производится опыт, в результате которого наступило событие А. Это вызовет переоценку вероятностей . Формулы Байеса и дают выражения для условных вероятностей ( называют гипотезами относительно события ).

Пример 5. На сборку поступают детали, изготовленные на двух заводах. Известно, что объем продукции первого завода в n раз превышает объем продукции второго завода. Доля брака на первом заводе составляет р₁, на втором – р₂ . Наугад взятая деталь оказалась бракованной. Какова вероятность того, что эта деталь изготовлена на первом заводе?

Решение. Пусть событие - «деталь изготовлена на первом заводе», – «деталь изготовлена на втором заводе» и – «наугад взятая деталь оказалась бракованной». Тогда

Подставляя сюда вероятности

получим

4.3. Независимость случайных событий

Понятие независимости событий играет, пожалуй, центральную роль в теории вероятностей: именно это понятие выделяет теорию вероятностей из общей теории измеримых пространств с мерой.

Определение. Два события и называются независимыми, если их условные вероятности совпадают с безусловными, т.е. вероятность наступления одного из них не зависит от того наступило другое событие или нет:

, .

При этом теорема умножения (4.2) примет вид

Р(АВ)=Р(А)Р(В). (4.5)

Впрочем, формула (4.5) принято считать за определение независимости двух событий.

Теорема 3. Если и – независимые события, то будут независимыми также события и

Докажем, что и независимы. Так как

Следовательно, и независимы.

Доказательство остальных свойств предоставляем читателю.

Определение. Случайные события называются независимыми в совокупности, если для любого и для любого набора индексов () имеет место равенство

События называются попарно независимыми, если при любых

Очевидно что, если независимы в совокупности, то любые два события также независимы, т.е. события попарно независимы. Однако, из попарной независимости не следует независимость в совокупности. В этом убеждаемся на следующем примере.

Пример С.Н. Бернштейна. На плоскость бросают тетраэдр, три грани которого окрашены соответственно в красный, зеленый, голубой цвета, а на четвертую грань нанесены все три цвета. Обозначим через К, З, Г – события, состоящие в том, что при бросании тетраэдра на плоскость выпадет грань с соответствующим цветом.

Так как каждый из трех цветов нанесен на две грани, то

Далее, , и , т.е. события К, З, Г попарно независимы.

Однако, , т.е. события К, З, Г не являются независимыми в совокупности.

Возникает естественный вопрос. Как же определить независимость событий на практике? Проверка выполнения формулы (4.5) – задача, во-первых, нелегкая. С другой стороны, , как правило, и нужно бывает вычислить, и проверять ее разложение ни к чему.

На практике часто при определении независимости исходят из физических соображений. Так, если некоторые события обусловлены физическими процессами, пренебрежимо слабо связанными между собой, то их можно считать независимыми.

Во многих случаях независимость событий определяют из соображений симметрии. Это, например, имеет место при рассмотрении различных событий, связанных с бросанием костей, монет, с раздачей игральных карт, с урновыми схемами. Основным требованием здесь является неизменность комплекса условий, при которых проводится эксперимент.

Различие физических процессов, с которыми связаны случайные события, однако, не является обязательным условием их независимости. Может быть и так, что события, связанные с одним и тем же физическим процессом независимы. Так, например, независимы различные элементы траектории частицы при моделировании процесса переноса излучений.

Упражнения к параграфу.

1. Бросают три игральные кости. Какова вероятность того, что по крайней мере на одной выпадает шестерка, если на всех трех костях выпали разные грани?

2. Известно, что 5% мужчин и 0,25% всех женщин – дальтоники. Наудачу выбранное лицо – дальтоник. Какова вероятность того, что это мужчина (считать, что мужчин и женщин одинаковое количество)?

3. Дано Р(А/В)= Р(В/А)=0,6.

Вычислить Р(А),

4. Доказать, что если Р(А)=0,9; Р(В)=0,8, то Р(А/В)0,875.

5. Доказать, что

6. Доказать, что , если Ø и .

7. Пусть и - независимые события и . Доказать, что либо , либо имеет вероятность, равную единице.

8. Пусть – попарно независимые события. Доказать, что

9. Стрелок попадает в мишень с вероятностью 0,6, стрелок – с вероятностью 0,5 и стрелок - с вероятностью 0,4. Стрелки сделали залп по мишени. Обнаружено два попадания. Что более вероятно: попал в мишень или нет?

10. Пусть всхожесть семян оценивается вероятностью 0,7. Какова вероятность того, что из двух посеянных семян взойдет какое-либо одно?

11. Из колоды карт (их 36) наугад вынимают 2 карты. Найти вероятность, что среди них окажется хотя бы одна "дама".

12. В урне 2 белых и 7 черных шаров. Из нее наудачу вынимают (без возврата) 2 шара. Какова вероятность того, что они оба будут разных цветов?

13. Три орудия стреляют в цель независимо друг от друга. Вероятность попадания в цель каждого равна 0,7. Найти вероятность попадания в цель: а) только одного из орудий; б) хотя бы одного.

14. Имеется два ящика, в каждом по 10 деталей; в первом ящике 8, во втором - 7 стандартных деталей. Из каждого ящика наудачу вынимают по одной детали. Найдите вероятность того, что обе вынутые детали окажутся стандартными.

15. Вероятность хотя бы одного попадания стрелка в мишень при трех выстрелах равна 0,992. Найдите вероятность промаха при одном выстреле.

16. Сколько раз нужно подбросить две игральные кости, чтобы вероятность по крайне мере одного появления шестерки была больше, чем ½?

17. В некоторой местности вероятность того, что погода в данный день будет такой же, как и в предыдущий, равна , если предыдущий день был дождливый и , если предыдущий день был не дождливый. Вероятность того, что 1-ый день года дождливый, равна . Найти вероятность того, что -ый день дождливый и предел этой вероятности при .

18. Имеется элементов, расположенных в некотором порядке. Случайным образом они переставляются. Какова вероятность того, что хотя бы один элемент окажется на своем месте?

19. Представим себе ячеек, в которые случайно размещаются различных частиц. Каждая частица может попасть в любую из ячеек. Найти вероятности следующих событий:

={в - ую ячейку попало частиц},

={хотя бы одна ячейка окажется пустой}.

20. При одном цикле осмотра радиолокационной станции, следящей за космическим объектом, объект будет обнаружен с вероятностью . Проведены независимых циклов осмотра. Какова вероятность того, что объект будет обнаружен?

21. Имеется m радиолокационных станций, каждая из которых за один цикл осмотра обнаруживает объект с вероятностью (независимо от других циклов и других станций). За время каждая станция успевает совершить циклов осмотра. Найти вероятности следующих событий:

={за время объект будет обнаружен по крайней мере одной станцией},

={объект будет обнаружен каждой станцией}.

16. Электрическая цепь собрана по схемам, изображенным на рис 5.

а) б)

в) г)

д)

Рис. 5

Пусть ={за время выйдет из строя -ый элемент цепи} и , .

Разные элементы выходят из строя независимо друг от друга. Вычислить вероятность выхода цепи из строя за время для каждой из указанных схем.

17. Для повышения надежности прибора он дублируется таким же прибором. Надежность прибора равна . При выходе из строя первого прибора происходит мгновенное переключение на другой прибор. Найти надежность этой системы приборов.

18. В урнах находятся шаров, из которых белые. Наудачу выбирают урну и из нее шар. Какова вероятность того, что он окажется белым.

19. Вероятность того, что молекула, испытавшая в момент столкновение с другой молекулой и не имевшая других столкновений до момента , испытает столкновение в промежутке и равна Найти вероятность того, что время свободного пробега молекулы будет больше t.

20. Два лица играют в «орла». Если выпадет та сторона монеты, которая была названа игроком, то он выигрывает 1 руб., в противном случае столько же проигрывает. В начале у игрока было руб. и он ставит целью довести свой капитал до суммы в руб. Игра продолжается до тех пор пока либо игрок наберет заветную сумму, либо разорится, проиграв весь свой капитал. Какова вероятность разорения игрока?

21. Расследуются причины неудачного запуска космических ракет, о которых можно высказать четыре предположения (гипотезы) . По данным статистики , , , . В ходе расследования обнаружено, что при запуске произошла утечка топлива (событие ). Условные вероятности события по той же статистике равны , , , . Какая из гипотез наиболее вероятна при данных условиях?

22. Числа натурального ряда , написанные на отдельных карточках, перемещали и расположили в случайном порядке. Какова вероятность того, что хотя бы одно число окажется на своем месте? Найти .

23. Три стрелка произвели по одному выстрелу по намеченной цели. Вероятность попадания 1-ым стрелком равна 0,6; 2-ым – 0,7; 3-им – 0,8. При одном попадании в мишень вероятность поражения цели равна 0,2; при двух – равна 0,6; при трёх – цель заведомо поражается. Найти вероятность поражения цели.

24. В сеансе одновременной игры в шахматы с гроссмейстером играют 10 перворазрядников и 15 второразрядников. Вероятность того, что в таком сеансе перворазрядник выиграет у гроссмейстера равна 0,2; для второразрядника эта вероятность равна 0,1. Случайно выбранный участник выиграл. Найти вероятность того, что это был второразрядник.

25. В первой урне содержится 10 шаров, из них 8 белых; во второй —20 шаров, из них 4 белых. Из каждой урны наудачу извлекли по одному шару, а затем из этих двух шаров наудачу взят один шар. Найти вероятность того, что взят белый шар.

26. В пирамиде пять винтовок, три из которых снабжены оптическим прицелом. Вероятность того, что стрелок поразил мишень при выстреле из винтовки с оптическим прицелом, равна 0,95; для винтовки без оптического прицела эта вероятность равна 0,7. Найти вероятность того, что мишень будет поражена, если стрелок произведет один выстрел из наудачу взятой винтовки.

27. В вычислительной лаборатории имеется Шесть клавишных автоматов и четыре полуавтомата. Вероятность того, что за время выполнения некоторого расчета автомат не выйдет из строя, равна 0,95; для полуавтомата эта вероятность равна 0,8. Студент производит расчет на наудачу выбранной машине. Найти вероятность того, что до окончания расчета машина не выйдет из строя.

28. В магазин поступили электрические лампочки одного типа, изготовленные на четырех ламповых заводах: с 1-го завода 250 шт., со 2-го — 525 шт., с 3-го — 275 шт. и с 4-го — 950 шт. Вероятность того, что лампочка прогорит более 1500 часов, для 1-го завода равна 0,15, для 2-го — 0,30, для 3-го — 0,20, для 4-го — 0,10. При раскладке по полкам магазина лампочки были перемешаны. Какова вероятность того, что купленная лампочка прогорит более 1500 часов?

29. Есть три завода, производящих одну и ту же продукцию. При этом первый завод производит 25%, второй завод — 35% и третий — 40% всей производимой продукции. Брак составляет 5% от продукции первого завода, 3% от продукции второго и 4% от продукции третьего завода. Вся продукция смешивается и поступает в продажу. Найти а) вероятность купить бракованное изделие; б) условную вероятность того, что купленное изделие изготовлено первым заводом, если это изделие бракованное.

30. Из урны, содержащей 3 белых и 2 черных шара, переложили 1 шар в урну, содержащую 4 белых и 4 черных шара. Какова вероятность того, что после этого из второй урны будет вынут белый шар.

31. На сборку поступают детали с двух автоматов. Первый дает в среднем 0,2% брака, второй – 0,1%. Найти вероятность попадания на сборку бракованной детали, если с первого автомата поступило 2000 деталей, а со второго 3000 деталей.

32. Из 20 стрелков 15 попадают в мишень с вероятностями 0,5; 5 стрелков – с вероятностями 0,8. Найти вероятность того, что наудачу выбранный стрелок попадет в мишень.

33. На заводе, изготовляющем болты, первая машина производит 25%, вторая - 35%, третья - 40% всех изделий. В их продукции брак составляет соответственно 5, 4 и 2%. Какова вероятность того, что случайно выбранный болт дефектный?

34. Прибор может работать в двух режимах: нормальном и ненормальном. Нормальный режим наблюдается в 80% всех случаев работы прибора; ненормальный – в 20%. Вероятность выхода прибора из строя за время в нормальном режиме равна 0,1, в ненормальном 0,7. Найти полную вероятность выхода прибора из строя за время .

35. Предположим, что 5 мужчин из 100 и 25 женщин из 10000 являются дальтониками. Наугад выбранное лицо страдает дальтонизмом. Какова вероятность того, что это мужчина?

36. В двух пакетах по 20 конфет одинаковой формы, в первом пакете 5 конфет с начинкой, а во втором - 8. Наугад выбранная конфета оказалась с начинкой. Какова вероятность того, что она была вынута из второго пакета?

37. Сборщик получил три коробки деталей, изготовленных заводом 1, и две коробки деталей, изготовленных заводом 2. Вероятность того, что деталь завода 1 стандартна, равна 0,9, а завода 2 - 0,8. Сборщик извлек стандартную деталь из наудачу взятой коробки. Какова вероятность того, что она изготовлена заводом №2?

38. Один из трех стрелков вызывается на линию огня и производит два выстрела. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0,3, для второго - 0,5; для третьего - 0,8. Мишень не поражена. Какова вероятность того, что выстрелы произведены первым стрелком?

39. В магазин поступила новая продукция с трех предприятий. Процентный состав этой продукции следующий: 20% - продукция первого предприятия, 30% - продукция второго предприятия, 50% - продукция третьего предприятия; далее, 10% продукции первого предприятия высшего сорта, на втором предприятии - 5% и на третьем - 20% продукции высшего сорта. Купленная новая продукция окажется высшего сорта. Какова вероятность того, что данная продукция принадлежит первому предприятию?

Контрольные вопросы

1. В чем различия условной и безусловной вероятностей?

2. Какие события называются независимыми?

3. Сформулируйте теорему умножения вероятностей.

4. При решении каких задач используется формула полной вероятности?

5. При решении каких задач используется формула Бейеса?

6. Выведите формулу Байеса.

§ 5. ПОСЛЕДОВАТЕЛЬНОСТИ НЕЗАВИСИМЫХ ИСПЫТАНИЙ

Пусть производятся последовательных испытаний (опытов), в каждом из которых происходит одно из событий с вероятностями

Испытания считаются независимыми, если вероятность появления события в –ом испытании не зависит от исходов предыдущих испытаний. Каждому такому испытанию сопоставим вероятностное пространствоF, где , F – состоит из всех подмножеств , а вероятность P определена для каждого события А_к равенством

Результату же опытов отвечает вероятностное пространство F, где , FF…F, а вероятность

(5.1)

5.1. Схема Бернулли. Биномиальное распределение вероятностей

Простейшим частным случаем последовательности независимых испытаний является, так называемая, схема Бернулли.

Пусть – случайное событие, которое является результатом опыта, проводимого при некотором комплексе условий . Отвлекаясь от множества всех исходов опыта, сосредоточим внимание на одном вопросе: в результате опыта происходит событие или не происходит. Таким образом, пространство элементарных событий , связанное с опытом мы сводим к двум событиям и составляющим, как видим, полную группу, т.е. (достоверное событие). Причем .

Рассмотрим пример с бросанием правильной игральной кости. Пусть – выпадение числа очков, равное 6. Тогда - это выпадение любой из остальных граней (1,2,3,4,5). Условимся считать появление события «успехом» и обозначать единицей, а появление «неудачей» и обозначать нулем. Пусть вероятность успеха , тогда вероятность неудачи . Приведенная простейшая схема независимых испытаний называется схемой Бернулли.

Интерес представляет, конечно, не один опыт, а множество его повторений в независимых условиях. Пространство элементарных событий , отвечающее результату таких испытаний, является прямым произведением пространств

а элементарное событие представляет собой последовательность нулей и единиц длины , причем на -ом месте в этой последовательности стоит 1 в случае «успеха» в –ом испытании или 0 в случае «неудачи»: . Число всех таких последовательностей (число всех элементов ) равно (доказать).

Согласно формуле (5.1) каждому элементарному событию ставится в соответствие вероятность.

(5.2)

где m– число единиц ((n-m)-число нулей) в последовательности .

В схеме Бернулли часто решается следующая задача:

Определить вероятность того, что в испытаниях ровно раз наступит «успех». Обозначим эту вероятность через

Теорема. Вероятность того, что в испытаниях схемы Бернулли ровно раз наступит «успех» (интересующее нас событие), определяется формулой

(5.3)

Доказательство. Обозначим через , последовательность (элементарное событие), в которой на -ых местах стоят «1», а на остальных местах «0». Число таких последовательностей, очевидно, равно числу способов выбора мест для «1», т. е. , а вероятность каждой из таких последовательностей равна (формула (5.2)).

Пусть – событие «в независимых испытаниях интересующее нас событие («успех») наступит ровно раз».

Ясно что – это подмножество элементарных событий указанного выше вида. Тогда согласно формуле (5.1) имеем:

что и требовалось доказать.

Пример 1. В урне 4 белых и 2 черных шара. Из урны извлекают шар, фиксируют его цвет, после чего шар обратно возвращают в урну. Такой опыт повторяют пять раз. Какова вероятность того, что в этих испытаниях белый шар появится ровно 2 раза.

Решение. Независимость испытаний обеспечивается неизменностью условий их проведения (извлеченный шар возвращается обратно). Вероятность извлечения белого шара («успех») при каждом испытании одна и та же и равна 4/6. Поэтому мы имеем дело со схемой Бернулли и по формуле (5.3) искомая вероятность равна

Если извлеченный шар больше не возвращать в урну, то испытания, очевидно, будут зависимыми: вероятность извлечения белого шара в последующем испытании зависит от исходов предыдущих испытаний.

Формула (5.3) называется формулой Бернулли, а совокупность вероятностей называют биномиальным законом распределения вероятностей.

Это название связано с тем, что выражение (5.3) является коэффициентом при в разложении бинома по степеням :

При вероятность совпадает с членом бинома Ньютона:

Таким образом,

Это же можно получить и из теоретико-вероятностных соображений. Действительно, вероятности представляют собой вероятности событий состоящих в появлении интересующего события в независимых испытаниях 0,1,2,…, раз. События образуют полную группу попарно несовместимых событий. Поэтому

Рассмотрим некоторые свойства вероятностей .

При n фиксированном представляет собой некоторую функцию аргумента k (k=0,1,…n) . Исследуем эту функцию. Найдем, в частности, при каком k функция принимает наибольшее значение. Для этого рассмотрим отношение

Это отношение может быть или больше, или меньше или равно 1:

а) если , то получим, что при ;

б) если , то при ;

в) и, наконец, если это отношение равно 1, то при .

Обозначим . Таким образом, при всех функция возрастает, а при - убывает, при .

Следовательно, вероятность с увеличением сначала возрастает, затем достигает максимума и при дальнейшем росте убывает. Если является целым числом, то функция принимает максимальное значение в двух точках: и . Если же нецелое число, то функция имеет единственный максимум; он достигается при ближайшем к справа (так как функция возрастает) целом значении , то-есть, при таком , которое заключено между и

Значение , при котором принимает максимальное значение, называется наиболее вероятным числом успехов в испытаниях Бернулли.

Пример 2. Монета подбрасывается 30 раз. Каково наиболее вероятное число выпадения герба?

Решение. В данном случае =30, =

Так как не является целым числом, то наиболее вероятное число выпадения герба будет 15.

5.2. Полиномиальное распределение вероятностей

Возвращаясь к общей схеме последовательности независимых испытаний, предположим, что при каждом испытании может произойти одно из событий причем вероятности этих событий равны соответственно , и не меняются от испытания к испытанию. Тогда имеет место

Теорема. Вероятность того, что в независимых испытаниях событие появится раз, событие раз,…, событие раз определяется формулой:

(5.4)

Доказательство. Пространство элементарных событий в данном случае представляет собой всевозможные последовательности событий длины , где индексы Обозначим через событие, состоящее в том, что в испытаниях событие появится раз, раз,…, раз, то-есть состоит из элементарных событий (последовательностей) , у которых на m₁ местах «стоят» событие , на местах – , и т.д., на местах – событие . Вероятность каждого равна

Число элементарных событий, входящих в B, можно подсчитать следующим образом. Исход на местах цепочки где - исход -го испытания, можно расположить способами; исход на из оставшихся мест способами и т.д. Таким образом, искомое число по принципу умножения в комбинаторике равно

Следовательно,

что и требовалось доказать.

Распределение вероятностей, определяемое формулой (5.4), называется полиномиальным распределением.

Название объясняется тем, что вероятность (5.4) является коэффициентом при в разложении полинома по степеням .

В физических задачах последовательность из n независимых испытаний, в каждом из которых может произойти одно из событий интерпретируется как размещение частиц по ячейкам; является вероятностью попадания частицы в –ю ячейку. Если , то говорят о равновероятном распределении частиц по ячейкам.

Пример 3. В урне содержится 5 белых, 3 черных и 2 красных шара. Производится 5 извлечений с возвращением. Найти вероятность того, что 3 раза появится белый и по одному разу черный и красный шары.

Решение. Каждое испытание (извлечение шара ) завершается одним из трех исходов: Б- появление белого, Ч – появление черного и К – появление красного шара. Вероятности этих событий в каждом испытании в схеме выборки с возвращением одинаковы и равны соответственно , , . Тогда для искомой вероятности имеем

5.3. Отрицательное биномиальное распределение

Со схемой Бернулли тесно связано решение задачи о числе испытаний, предшествующих -ому успеху. Речь идет о вероятности того, что для достижения успехов потребуется испытаний.

Искомая вероятность (обозначим ее ) есть вероятность того, что в серии из опытов, в каждом из которых некоторое событие может появиться с вероятностью («успех») и не появиться с вероятностью («неудача»), будет равно неудач, а следующее -ое испытание приведет к успеху, т.е.

(5.5)

Формула (5.5.) определяет так называемое отрицательное биномальное распределение (Распределение Паскаля).

Название связано с тем, что распределение можно записать в виде

где

При из (5.5.) получим распределение вероятностей

(5.6)

называемое геометрическим. Оно определяет вероятность того, что потребуется испытаний до наступления «успеха» в первый раз. Если считать, что каждое испытание длится единицу времени, то можно считать временем ожидания до первого успеха.

Пример 4. Имеется партия изделий некоторого производства. Пусть доля возможного брака составляет 0,2%. Определить вероятности следующих событий: - «среди выбранных для контроля 10 изделий не менее 9 исправных»; - «для обнаружения брака придется проверить ровно 10 изделий».

Решение. Выбор изделий из большой партии можно считать независимыми испытаниями с вероятностью «успеха» .

Тогда

Вероятность события В находим по формуле (5.6).

5.4. Предельные теоремы в схеме Бернулли и их применения

Рассмотрим еще некоторые примеры, связанные со схемой независимых испытаний.

Пример 5. Производится профилактический осмотр жителей города с 10 000 населением, подозреваемого в том, что он оказался в полосе прохождения радиоактивного облака. Какова вероятность того, что будет обнаружено 40 заболевших, если вероятность заражения для каждого жителя .

Решение задачи укладывается в схему независимых испытаний Бернулли: , и .

По формуле (5.3) находим

Пример 6. Для контроля качества из всей партии продукции некоторого предприятия взяты 1000 изделий. Причем каждое изделие в партии может быть дефектным с одинаковой вероятностью независимо от других. Вся партия будет принята, если количество диффектных изделий в выборке составит не более 20. Определить вероятность того, что партия продукции будет принята.

Решение. Событие представляет собой сумму несовместимых событий

Поэтому

Эти примеры приведены, чтобы подчеркнуть трудности, которые возникают при подсчете вероятностей при больших значениях по точной формуле Бернулли (5.3). Вычисления становятся еще труднее, если необходимо найти вероятность

где , - целые числа.

А между тем, именно с такими ситуациями приходится иметь дело при решении практических задач.

Поэтому возникла необходимость в создании асимптотических, приближенных формул для этих целей. Впервые эта задача была решена французским математиком А.Муавром (1667-1754).

Локальная теорема Муавра. В испытаниях Бернулли при имеет место

(5.7)

равномерно для всех m , для которых величина

принадлежит некоторому конечному отрезку .

Доказательство опирается на известную формулу Стирлинга

где

Из условия теоремы видно, что и возрастают до бесконечности вместе с при

Имеем:

(5.8)

где

при , т.к. и тоже возрастают вместе с .

То-есть в (5.8) множитель при равномерно по всем .

Рассмотрим квадратный корень в (5.8):

(5.9)

равномерно по .

Наконец, рассмотрим квадратную скобку в (5.8) и прологарифмируем ее, заменяя и своими выражениями:

(5.10)

Здесь использовано разложение Утверждение теоремы следует из соотношений (5.8), (5.9), (5.10) и

Доказанная теорема дает оценку величины при больших ;

(5.11)

Функция

называется функцией Гаусса; она затабулирована. Используя таблицы этой функции, нетрудно находить приближенные значения при больших .

Сейчас мы сможем вернуться к примеру 1 и найти оценку вероятности , пользуясь приближенной формулой (5.11). Здесь , , , ,

Таким образом,

Значение находим по таблице: Тогда

Пример 7. Монету бросают 1000 раз. Какова вероятность того, что при этом «герб» выпадает ровно 500 раз?

Решение: , , , ; наивероятнейшее число также равно 500; .

Интегральная предельная теорема Муавра – Лапласа. Пусть - число наступления некоторого события в независимых испытаниях с вероятностью появления этого события в каждом испытании, причем Тогда при имеет место соотношение

причем стремление является равномерным относительно и

Доказательство теоремы можно установить, используя локальную теорему Муавра, но проще его получить как простое следствие центральной предельной теоремы (см. §11).

Практическое применение этой теоремы заключается в том, что из нее можно получить приближенную формулу для вероятности

Действительно, при больших имеем:

, (5.12)

где

(5.13)

Для функции построены специальные таблицы, так как интеграл в (5.13) невозможно выражать через элементарные функции. Эти таблицы приводятся в учебниках и задачниках по теории вероятностей и математической статистике только для положительных х. Для отрицательных значения функции определяются из ее свойства нечетности: .

Заметим также, что график функции проходит через начало координат и прямые и являются ее асимптотами.

Закончим теперь пример 2 этого параграфа.

Имеем:

, ,

Следовательно:

Приведем некоторые типичные задачи, приводящие к интегральной теореме Муавра – Лапласа.

1) Чему равна вероятность того, что частота наступления события в независимых испытаниях отклонится от вероятности не более, чем на ?

Эта вероятность равна

так как - нечетная функция.

Учитывая указанные выше свойства функции , нетрудно получить следующий факт:

, (5.14)

который известен как теорема Бернулли или закон больших чисел в форме Бернулли. Этому важнейшему закону теории вероятностей посвящен отдельный параграф. Там же утверждение (5.14) будет доказано исходя из других соображений.

2) Какое наименьшее число испытаний нужно провести для того, чтобы с вероятностью, не меньшей , частота события отклонялась от вероятности не больше, чем на .

Требуемое число испытаний определяется из неравенства

Используя соотношение из предыдущего примера, получим

где все величины известны, кроме . Пусть - найденное из таблиц значение аргумента, соответствующее значению функции , равное . Тогда искомое значение находим из соотношения .

3) При данной вероятности и числе испытаний требуется определить границу возможных изменений , т.е. требуется найти

Решение задачи находим также из соотношения

Замечание о точности приближенных формул. Точность формул (5.11) и (5.12) существенно зависит от величины . При или близком к нулю эти формулы дают значительную погрешность. Этот случай был рассмотрен французским математиком С. Пуассоном (1781-1840).

Теорема Пуассона. Пусть и при - фиксировано. Тогда

Доказательство. Полагая получим:

Переходя к пределу здесь при в каждом множителе, получим

Определение. Распределение вероятностей, определяемое формулой

(5.15)

называется распределением Пуассона и является одним из важнейших в теории вероятностей и ее приложениях.

Замечание. Для вычисления вероятностей по формуле (5.15) вовсе не требуется знания и , все определяется параметром , который представляет собой среднее число успехов в независимых испытаниях.

Решение некоторых задач.

1. Известно, что вероятность рождения мальчика приблизительно равна 0,515. Какова вероятность того, что среди 10000 новорожденных число мальчиков будет не больше, чем число девочек,

Решение. По условию , . Требуется вычислить , где - число мальчиков.

Используем приближенную формулу (5.12):

2. Модель радиоактивного распада. Радий обладает свойством распадаться (превращаться в радон), излучая -частицы. Можно предположить, что распад отдельного атома радия происходит независимо от состояния других атомов и вероятность распада отдельного атома в некотором промежутке времени зависит лишь от длины этого промежутка. Пусть - вероятность распада в течение времени длины . Если имеется всего n атомов радия ( в одном грамме насчитывается приблизительно 10²² атомов), то среднее число - частиц, испускаемых за время , равно Многочисленные эксперименты показали, что это число при сек. имеет порядок 10¹⁰ , так, что вероятность является очень малой (при сек. P(t) имеет порядок 10^-12). Если m - число испускаемых за время - частиц, то P()

3. Блуждание частицы по прямой.. Пусть некоторая частица, находящаяся в начальный момент в точке , под влиянием случайных толчков блуждает по прямой перемещаясь на единицу масштаба вправо с вероятностью и влево – с вероятностью . (При случайное блуждание называется симметричным). Считая перемещение вправо на единицу успехом, а влево – неудачей, мы имеем здесь дело со схемой Бернулли.

Найдем вероятность того, что за шагов частица переместится на расстояние .

Решение. Если обозначить число «успехов» через , то точка переместится за n шагов на расстояние Тогда

при одинаковой четности и .

Если же и разной четности, то - нечетное число и и.

При симметричном блуждании из теоремы Муавра получаем:

(5.16)

Формулу (5.16) можно интерпретировать следующим образом. Пусть в начальный момент в точке =0 имеется большое число частиц, которые независимо друг от друга начинают перемещаться по прямой под влиянием случайных толчков. Тогда эта формула определяет долю частиц, переместившихся на расстояние после толчков.

Упражнения к параграфу.

1. При передаче сообщения вероятность искажения одного знака равна 0,1. Какова вероятность того, что сообщение из 10 знаков: а) не будет искажено, б) содержит ровно 3 искажения, в) содержит не более трех искажений?

2. Вероятность попадания в мишень при одном выстреле для стрелка равна 0,6. Стрелок производит 5 выстрелов. Каковы вероятности следующих событий: а) при этой стрельбе произойдет два попадания, б) в мишень попадут больше 3 выстрелов. Найдите наиболее вероятное число попаданий и соответствующую этому числу вероятность.

3. Доказать рекуррентную формулу для биномиальных вероятностей:

С помощью этой формулы решите задачу:

Два равносильных шахматиста играют ряд партий, причем ничьи не учитываются. Какой счет более вероятен: (1:1), (2:2) или (3:3)?

4. В круг вписан правильный треугольник. Найти вероятность того, что из 5 наудачу брошенных в круг точек ни одна не упадет внутрь указанного треугольника.

5. Опыт состоит в делении заданного отрезка случайным образом на 3 части. Производится 6 таких независимых опытов. Какова вероятность того, что в двух случаях из полученных частей отрезка можно составить треугольник?

6. Испытание состоит в бросании двух игральных костей. Найти вероятность того, что в 5 таких бросаниях ровно 2 раза выпадет по две шестерки.

7. При передаче сообщения вероятность искажения каждого знака равна 0.01. Предполагая независимость искажения любого из знаков, найти вероятность того, что группа из 5 знаков а) не будет искажена; б) будет содержать менее двух искажений.

8. Какое из событий более вероятно: а) появление по крайне мере одной шестерки при бросании 6 игральных костей; б) появление хотя бы 2 раза шестерок при бросании 12 костей; в) появление хотя бы 3 шестерок при бросании 18 игральных костей.

9. Вероятность изготовления стандартной детали 0,95. Сколько деталей должно быть в партии, чтобы наиболее вероятное число стандартных деталей в ней было 55?

10. Мишень имеет форму квадрата, в который вписан круг. По мишени наудачу производится 4 независимых выстрела. Какова вероятность получения трех попаданий в круг?

11. Задача Банаха. Некий математик носит с собой две коробки спичек. Каждый раз, когда он хочет достать спичку, он выбирает наудачу одну из коробок. Найти вероятность того, что когда математик вынет пустую коробку, в другой окажется спичек (; - число спичек в каждой коробке первоначально).

12. На контроль поступила партия деталей из цеха. Известно, что 5% всех деталей не удовлетворяют стандарту. Сколько нужно испытать деталей, чтобы с вероятностью не меньшей 0,95 обнаружить хотя бы одну нестандартную деталь?

13. Вероятность того, что частица будет зарегистрирована счетчиком равна 10^-4. Какое наименьшее число частиц должно вылететь из источника, чтобы с вероятностью 0,99 счетчик зарегистрировал хотя бы одну частицу?

14. Вероятность рождения мальчика примерно равна 0,5. Найдите вероятности следующих событий:

а) среди 200 новорожденных детей будет 100 мальчиков.

б) среди 200 новорожденных детей мальчиков будет от 90 до 110.

15. На факультете 730 студентов. Вероятность рождения каждого студента в данный день равна Найти вероятность того, что найдутся три студента с одним и тем же днем рождения.

16. Завод отправил на базу 5000 доброкачественных изделий. Вероятность повреждения каждого изделия в пути равна 0,0002. Найдите вероятность того, что из 5000 изделий в пути будет повреждено:

а) ровно 3 изделия, б) не более 3 изделий, в) более трех изделий.

17. В страховом обществе зарегистрировано 10000 лиц одного возраста и одной социальной группы. Вероятность смерти в течении года для каждого лица равна 0,006. Каждый застрахованный вносит 1 января 1200 руб страховых, и, в случае смерти, его родственники получают от общества 100000 руб. Найдите вероятности событий:

а) страховое общество потерпит убыток;

б) страховое общество получит прибыль не меньшую 5000000 руб.

18. В водоем выпущено 100 меченых рыб. Вскоре после этого из водоема было выловлено 400 рыб, среди которых оказалось 5 меченых. Определить общее количество рыб в водоеме с вероятностью 0,9.

19. Опыт состоит в бросании монеты 4040 раз (опыт Бюффона), причем герб выпал 2048 раз. Найдите вероятность того, что при повторении этого опыта частота появления герба отклонится от 0,5 не более, чем в опыте Бюффона.

20. Театр, вмещающий 1000 человек, имеет два разных выхода. Около каждого из выходов имеется свой гардероб. Сколько мест должно быть в каждом из гардеробов для того, чтобы в среднем в 99 случаях из 100 все зрители могли раздеться в гардеробе того выхода, через который они вошли.

21. В электропоезд, состоящий из шести вагонов, наугад садятся 12 человек. Определить вероятности следующих событий:

а) в каждый вагон вошло по 2 человека;

б) в один вагон никто не вошел, в другой – один человек, в два вагона – по два человека, а в оставшиеся два вагона соответственно три и четыре человека.

22. В круг вписан квадрат. Найдите вероятность того, что из 10 точек, брошенных наудачу независимо одна от другой внутрь круга, 4 попадут в квадрат, 3 – в один сегмент и по одной – в оставшиеся 3 сегмента.

Контрольные вопросы

1. Какие испытания называются независимыми?

2. При решении каких задач используется формула Бернулли?

3. Дайте определение биномиального и полиномиального распределеня вероятностей.

4. Сформулируйте условия применимости формулы Пуассона в схеме Бернулли.

5. Когда следует применять локальную и интегральную теоремы Муавра-Лапласа.

§ 6 ЦЕПИ МАРКОВА

Так называется простейший вариант последовательности зависимых испытаний, изученных впервые выдающимся русским математиком А.А. Марковым (1856-1922 гг.)

Цепи Маркова являются математической моделью многих случайных явлений. Их интенсивное изучение привело к созданию достаточно развитой теории, так называемых, марковских случайных процессов.

В схеме Бернулли, изученной в предыдущем параграфе, рассматривалась последовательность из конечного числа n независимых испытаний, каждое из которых завершалось одним из двух возможных исходов. Теперь обобщим эту схему. Производится неограниченная последовательность испытаний, каждое из которых завершается одним из попарно несовместимых исходов . Испытания эти связаны следующей зависимостью: вероятность наступления любого из указанных исходов в -ом испытании зависит от исхода предыдущего –го испытания и не зависит от исходов более ранних испытаний.

При изложении теории цепей Маркова удобна другая терминология.

Имеется некоторая физическая (или другая) система, которая может находиться в одном из состояний . В целочисленные моменты времени под влиянием случайных факторов происходит смена состояний (переход из одного состояния в другое) Вместо того чтобы говорить «в результате –го испытания произошло событие » говорят, что « в момент времени t_m система оказалась в состоянии ».

Дадим теперь формальное определение цепи Маркова. Обозначим состояние системы в момент через .

Определение. Последовательность переходов системы из одного состояния в другое образует цепь Маркова, если вероятность перехода системы в состояние в момент зависит от состояния , в котором она находилась в непосредственно предыдущий момент времени и не зависит от состояний, в которых система находилась в более ранние моменты времени, т.е. имеет место равенство (марковское свойство):

Условные вероятности будем обозначать через и называть переходными вероятностями.

Цепь Маркова называется однородной, если переходные вероятности зависят только от разности моментов времени, т.е., если для любых

Мы ограничимся рассмотрением однородных цепей Маркова. Обозначим - вероятность перехода системы из одного состояния в другое за время (или за шагов).

Тогда , называются вероятностями перехода за один шаг. Эти вероятности образуют матрицу

называемую матрицей перехода за один шаг.

Сумма элементов строки этой матрицы равна единице, а сами элементы неотрицательны. Такие матрицы называются стохастическими.

Цепь Маркова считается заданной, если известна матрица перехода и начальные вероятности , характеризующие состояния системы в начальный момент времени:

Рассмотрим несколько примеров.

Пример 1. Имеются две урны. В урне №1 находятся 9 белых и 1 черный шар, в урне №2 находятся 3 белых и 2 черных шара. В первый момент времени извлекается шар из урны №1, фиксируется цвет вынутого шара и шар возвращается в урну №1. В каждый последующий момент времени происходит извлечение шара из урны №1, если в предыдущем испытании появился белый шар (событие ), или урны №2, если в предыдущем испытании появился черный шар (событие ). Каждый раз извлеченный шар возвращается в ту урну, откуда он и был извлечен. Здесь мы имеем цепь Маркова с матрицей перехода

где - есть условная вероятность исхода в данном испытании, при условии, что в предыдущем испытании произошло событие .

Пример 2. Пусть по точкам , прямой блуждает частица под действием случайных толчков. Каждый толчок перемещает частицу на единицу длины вправо с вероятностью и влево с вероятностью . Если же частица окажется в точках то она остается в этих точках (говорят, что в этих точках поставлены поглощающие экраны).

Матрица перехода в этом случае имеет вид

Здесь - вероятность перехода частицы за один шаг из точки в точку

Пример 3. Аналогично можно описать блуждание частицы с отражением, когда в точках и поставлены отражающие экраны. Если частица окажется в указанных точках, то любой толчок переводит ее на единицу вовнутрь.

В этом случае матрица перехода имеет вид

6.1. Вероятности перехода

Выше мы определили как вероятности перехода системы из одного состояния в другое за один шаг.

Матрица перехода характеризует эволюцию системы за один шаг.

Теперь изучим эволюцию системы за время (за шагов), т.е. мы хотим определить вероятности перехода системы из в состояние за шагов. Эти вероятности мы обозначим через . Рассмотрим некоторое промежуточное число шагов . За это время система из состояния перейдет в одно из возможных состояний , , а затем из этого состояния в состояние за оставшееся число шагов . Вероятность перехода , очевидно, равна по формуле умножения вероятностей

Полная вероятность перехода по правилу сложения равна

(6.1)

Обозначим через матрицу перехода за шагов

. (6.2)

Согласно формуле (6.1) матрицу (6.2) можно записать в виде произведения соответствующих матриц и :

Откуда, при =2 находим матрицу перехода за 2 шага

при =3

и т.д.,

при любом

Таким образом, матрица перехода за t шагов представляет собой t-ую степень матрицы перехода за один шаг.

6.2. Эргодическая теорема

Другой важной задачей теории цепей Маркова является исследование поведения вероятностей при неограниченном возрастании . Приведем здесь теорему Маркова, называемую эргодической или теоремой о предельных вероятностях.

Теорема. Если при некотором числе шагов все элементы , то существуют такие постоянные числа , что независимо от индекса имеют место равенства

, (6.3)

Доказательство этой теоремы мы не приводим. Отметим только ее физический смысл: вероятность того, что система окажется в состоянии практически не зависит от того, в каком состоянии она находилась в далеком прошлом.

Возникает вопрос: если существуют предельные вероятности , то каким образом их найти?

Покажем, что является единственным решением системы уравнений

(6.4)

Действительно, исходя из формулы (6.1), имеем

(6.5)

Переходя к пределу в обеих частях равенства (6.5) при согласно (6.3) получим

. (6.6)

Так как то переходя к пределу здесь при получим .

Таким образом, числа удовлетворяют системе (6.4). Остается показать, что она имеет единственное решение.

Пусть также удовлетворяют системе (6.4). Тогда имеют место следующее равенства

т.е. для любого

Переходя к пределу при , получим

( по предположению).

Что и требовалось показать.

Упражнения к параграфу.

1. Вероятности перехода даются матрицей

Чему равно число состояний? Найти вероятности перехода за два шага.

2. Электрон может находиться на одной из счетного множества орбит в зависимости от энергии. Переход с –ой орбиты на –ю происходит за одну секунду с вероятностью

Найти: а) вероятности перехода за две секунды;

б) постоянные .

3. Вероятности перехода даются матрицей

Применима ли к такой цепи эргодическая теорема? Если да, то найти предельные вероятности.

4. На письменном столе лежит стопка из n книг с номерами от 1 до n . Каждая книга берется с определенной вероятностью (книга с номером k берется с вероятностью ,), причем при возвращении она кладется сверху стопки. Описать цепь Маркова, состояниями которой являются всевозможные перестановки вида (), где – номеp книги, лежащей сверху, …, -номер книги, лежащей в самом низу (рассмотреть случаи и ).

5. Доказать, что стохастическая матрица второго порядка является матрицей вероятностей перехода за два шага некоторой цепи Маркова тогда и только тогда, когда сумма ее диагональных элементов больше или равна единице.

6. Определить при каких значениях с и d цепь Маркова определяется однозначно начальным распределением и матрицей перехода за два шага:

7. Цепь Маркова имеет матрицу вероятностей перехода за один шаг

найти матрицу перехода за шагов и предел при .

Контрольные вопросы

1. Что образует цепь Маркова?

2. Дайте определение матрице перехода.

3. Как найти предельные вероятности?

§7. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ И ИХ РАСПРЕДЕЛЕНИЯ

В предыдущих параграфах мы неоднократно встречали величины, связанные с некоторыми опытами, значения которых зависели от случая и предсказать их заранее было невозможно.

Приведем несколько примеров:

1. Проверяется качество партии из N изделий. Известно, что при правильно организованном техническом цикле брак не может превышать m процентов. Для проверки из партии берут изделий. Число бракованных среди них зависит от многих факторов и нельзя заранее предсказать.

2. В последовательности независимых испытаний Бернулли нельзя заранее сказать сколько раз наступит интересующее нас событие.

3. Производится последовательность испытаний до первого появления некоторого события . Число испытаний случайно и может быть любым.

4. В теории стрельбы известно такое понятие, как «рассеивание» снарядов. Предположим, что производится стрельба из одного и того же орудия при неизменных условиях стрельбы (прицел, место, стрелок и др.) Расстояние до места падения снаряда будет различным при различных выстрелах из-за множества случайных факторов, предварительно не поддающихся учету.

5. Скорость молекулы газа меняется от столкновений с другими молекулами. Ввиду того, что на этот процесс оказывают влияние многие физические факторы, имеющие случайный характер, величина скорости является случайной.

Приведенные примеры являются примерами так называемых случайных величин.

Зададимся вопросом: что необходимо знать о случайной величине, чтобы считать ее задание известным и можно было использовать ее в научных или практических исследованиях? Чтобы ответить на этот вопрос, рассмотрим следующие две случайные величины.

Пусть подбрасывается правильная игральная кость. Пространство элементарных событий для этого опыта

Положим , то-есть величинa равна числу выпавших очков. Заранее, до подбрасывания кости, мы не можем сказать какая же грань выпадет. Результат эксперимента случаен, значение величины случайно. Однако, какие значения эта величина может принимать в результате эксперимента мы хорошо знаем:

=1,2,3,4,5,6.

Разделим рулеточный круг радиуса R на 6 частей пропорционально числам 1,2,3,4,5,6. Раскручиваем рулетку и отмечаем сектор, который остановился напротив стрелки. Пространство элементарных событий здесь такое же, как в эксперименте с подбрасыванием кости. Функцию от элементарных событий введем также, как в предыдущем примере

где - число очков, соответствующее указанному сектору. Величина принимает такие же значения, как и :

=1,2,3,4,5,6.

В чем же разница между и ? Разница – в частотах, с которыми значения 1,2,3,4,5,6 принимаются величинами и . В первом случае любое из значений 1,2,…,6 величина принимает с одной и той же вероятностью 1/6, то есть , . Во втором же примере величина принимает такие же значения, что и , но с совершенно другими вероятностями: , .

Разобранные выше примеры показывают, что для задания случайной величины недостаточно знать только ее возможные значения. Необходимо указать также как часто те или иные значения она принимает. В дискретном случае можно указать вероятности, с которыми случайная величина принимает свои возможные значения. Для непрерывной случайной величины, как будет показано позже, вероятность принять какое-то конкретное значение равна нулю. Для вероятностного выражения непрерывных случайных величин используются специальные функции.

Таким образом, интуитивное определение случайной величины можно дать следующим образом: случайной называется такая величина, значения которой меняется случайным образом от одного испытания к другому, причем можно указать вероятности или закон задания вероятностей реализации этих значений.

Случайные величины будем обозначать далее греческими буквами (с индексами или без них), а принимаемые ими значения соответствующими латинскими буквами.

Строгое математическое определение понятия случайной величины основано на рассмотрении вероятностного пространства F

Определение. Случайной величиной называется функция , определенная на множестве элементарных событий и измеримая относительно алгебры F.

Пусть - некоторое множество элементарных событий, - множество значений , измеримое по Борелю. Данное определение требует, чтобы F , то-есть было событием, и чтобы для него была определена вероятность

При , где - произвольное действительное число, вероятность . Таким образом, каждой случайной величине можно сопоставить функцию

, (7.1)

определенную на всей числовой оси и называемую функцией распределения (ф.р.) случайной величины.

7.1. Свойства функции распределения

1. Если известна функция распределения случайной величины , то

(7.2)

Доказательство. Рассмотрим события

Тогда , причем Ø.

Значит

или

, откуда следует (7.2).

2. Функция распределения является неубывающей функцией, то-есть

Свойство следует из (7.2) и из того, что вероятность есть величина неотрицательная.

Следует из определения

Говорят, что функция имеет в точке скачок величины , если

4.Функция распределения имеет не более чем счетное множество скачков.

Доказательство. Очевидно, что скачков, величина С₀ которых больше ½, функция распределения согласно свойству 3 может иметь не более одного; скачков не более трех и т.д., скачков - не более . Ясно, что все эти скачки можно пронумеровать, начиная с больших значений и повторяя равные значения столько раз, сколько таких скачков функция имеет.

5.;

Доказательство.

Рассмотрим последовательности и такие, что убывает, , а последовательность возрастает, . Пусть - последовательности событий, причем Ø. Тогда по аксиоме непрерывности , и, так как функция монотонная, .

Аналогично, достоверное событие.

Тогда согласно расширенной аксиоме сложения . Откуда следует, что

или .

6. Функция распределения непрерывна слева:

Доказательство. Пусть возрастающая последовательность, сходящаяся к , . Тогда и . Следовательно, Учитывая, что возрастающая функция получим:

Таким образом, каждая функция распределения является неубывающей, непрерывной слева и удовлетворяющей условиям

функцией.

Верно и обратное: удовлетворяющая перечисленным свойствам функция, может рассматриваться как функция распределения некоторой случайной величины.

Необходимо заметить, что в то время как каждая случайная величина однозначно определяет свою функцию распределения, существует сколько угодно случайных величин имеющих одну и ту же функцию распределения. Например, пусть с вероятностями , а .

Эти случайные величины, хотя и отличаются друг от друга, имеют одну и ту же функцию распределения

7.2. Дискретные случайные величины

Вернемся к примерам, приведенным в начале данного параграфа. В примерах 1 и 2 число значений, принимаемых случайной величиной, конечно, в третьем – случайная величина может принять счетное множество значений.

Определение. Случайные величины, принимающие только конечное или счетное множество значений, называются дискретными.

Дискретная случайная величина полностью определяется заданием принимаемых ею значений ,… и набора соответствующих вероятностей , , который называется распределением случайной величины .

Часто распределение дискретной случайной величины представляют, так называемым, рядом распределения – таблицей вида

			….		…
			….		…

где в верхней строке приводятся значения, принимаемые случайной величиной, а в нижней – вероятности этих значений, причем .

Функция распределения дискретной случайной величины определяется равенством

(7.3)

Рассмотрим основные дискретные распределения

1. Наиболее простой является случайная величина, связанная со схемой Бернулли: производится последовательность независимых испытаний, в каждом из которых некоторое событие может появиться с вероятностью и не появиться с вероятностью . Каждое такое испытание можно описать случайной величиной , принимающей значение 1, если событие произошло и 0 в противном случае:

	0	1

(7.4)

Назовем ее случайной величиной Бернулли. Таким образом, последовательность Бернулли представляет собой последовательность независимых случайных величин каждая из которых имеет распределение (7.4).

В схему Бернулли укладываются эксперименты: бросание игральной кости или монеты; проверка по альтернативному признаку изделий массовой продукции; обращение к обслуживающему устройству, у которого исходы «свободен» и «занят»; стрельба по цели – «попал» или «промах» и т.д.

2. Биномиальное распределение. Имеется последовательность независимых испытаний Бернулли. Пространство элементарных событий - это последовательность из единиц (событие произошло) и нулей ( не произошло). Функция - число наступления события в независимых испытаниях:

(7.5)

Нетрудно видеть, что биномиальную случайную величину можно представить как сумму случайных величин Бернулли типа (7.4), описывающих -ое испытание:

. (7.6)

Распределение (7.5) встречается: в теории и практике статистического контроля качества продукции; при описании работы системы массового обслуживания; в теории стрельбы и других областях практической деятельности.

3. Отрицательное биномиальное распределение.

Рассмотрим случайную величину , связанную с испытаниями Бернулли ,… следующим образом:

, , (7.7)

иначе говоря, - это число испытаний в схеме Бернулли (с вероятностью появления события в одном испытании) до -го «успеха»-появления интересующего нас события: случайная величина принимает значения с вероятностями

(7.8)

Отрицательное биномиальное распределение применяется: в статистике несчастных случаев и заболеваний, в биологии, в задачах оптимального резервирования элементов, в теории стрельбы и т.д.

4. Геометрическое распределение.

Пусть проводится неограниченное число испытаний по схеме Бернулли с вероятностью «успеха» р. Случайная величина - число испытаний до первого успеха включительно:

(7.9)

Геометрическое распределение получается из отрицательного биномиального распределения при

5. Гипергеометрическое распределение.

Пусть из совокупности в N элементов, среди которых элементов с определенным свойством, делается выборка объема . Случайная величина - число элементов с этим свойством в данной выборке:

(7.10)

Это распределение часто используется при статистическом контроле качества промышленной продукции при ее приемке, а также во многих других случаях, когда по выборочным данным делаются какие-то суждения.

6. Усеченное геометрическое распределение.

Случайная величина вводится так же, как и при геометрическом распределении с тем только отличием, что проводится ограниченное число испытаний. Тогда вероятности

при ,

. (7.11)

7. Распределение Пуассона.

Случайная величина - число наступления некоторого случайного события за единицу времени, когда наступление или ненаступление события не зависит от того, сколько раз и в какие моменты времени оно осуществлялось в прошлом, а испытания проводятся в стационарных условиях. Она принимает значения 0,1,2,…, с вероятностями

(7.12)

Это задание вероятностей называется пуассоновским распределением. Ранее в §5 было показано, что распределение (7.12) является предельным случаем для биномиального распределения, когда вероятность появления некоторого события в единичном эксперименте очень мала, но число экспериментов , производимых в единицу времени, достаточно велико. Мы видим, что распределение (7.12) зависит только от одного параметра . Позже мы покажем, что - это среднее число осуществления интересующего нас события в единицу времени.

Пуассоновская случайная величина используется для описания числа сбоев в автоматической линии или отказов сложной системы в единицу времени; числа требований на обслуживание, поступивших в единицу времени в систему массового обслуживания; закономерностей различных редких случаев (несчастных случаев, редких заболеваний) и др.

7.3. Непрерывные случайные величины

В примерах 4 и 5, приведенных в начале главы, невозможно перечислить принимаемые случайной величиной значения, они заполняют некоторые интервалы. Таким образом, эти случайные величины нельзя задавать, как дискретные случайные величины, перечислением принимаемых ими значений и соответствующих вероятностей. Более того, как мы увидим позже, вероятность конкретно взятого значения , для таких случайных величин оказывается равна нулю.

Для дискретной случайной величины мы видели, что функция распределения имеет скачки в точках (число таких скачков не более, чем счетно).

Определение. Случайная величина называется непрерывной, если ее функция распределения непрерывна при всех значениях .

Распределение дискретной случайной величины определяется заданием совокупности вероятностей

Аналогом для них в непрерывном случае является функция , называемая плотностью распределения вероятностей и определенная на всей числовой прямой.

Если же продолжить эту аналогию и операцию суммирования, применяемую для дискретной случайной величины, заменить на интегрирование, то в соответствии с (7.3) функция распределения непрерывной случайной величины выражается как интеграл

(7.13)

Определение. Случайная величина называется непрерывной, если для нее существует такая неотрицательная функция , что при любых выполняется (7.13).

Функция обладает следующими свойствами:

Пользуясь свойством 2) можно с точностью до бесконечно малых высших порядков написать, что

При неограниченном уменьшении интервала, т.е. стягивания в точку , . Таким образом, для непрерывной случайной величины вероятность принять конкретное значение равна нулю.

Примеры основных непрерывных распределений

1. Равномерное распределение.

Случайная величина называется равномерно распределенной в промежутке , если ее плотность распределения постоянна. Согласно свойству 3) плотности вероятности, получим

(7.14)

Функция распределения, соответствующая этой плотности, есть

(7.15)

На рис. 5 и рис. 6 указаны графики плотности и функции распределения случайной величины с равномерным распределением.

Рис. 5. Рис. 6.

Равномерное распределение находит применение: при анализе ошибок округления при проведении числовых расчетов – такая ошибка равномерно распределена от -5 до +5 единиц округляемого десятичного знака; при описании и решении различных задач, связанных с временем ожидания «обслуживания», когда обслуживающее устройство включается через точно определенные промежутки времени и когда заявка на обслуживание в этом промежутке тоже случайна (например, время ожидания пассажиром прибытия электрички, когда они ходят через определенный интервал и момент прихода пассажира в этот промежуток случаен, имеет равномерное распределение от 0 до ).

Особую роль играет случайная величина, равномерно распределенная в интервале [0,1].

Пусть - случайная величина с функцией распределения . Тогда оказывается, что случайная величина распределена равномерно в интервале [0,1]. Действительно:

Таким образом, , то есть совпадает с функцией распределения равномерной в [0,1] случайной величины (см. (7.15)).

Преобразование часто применяется при статистическом анализе, когда бывает удобно перейти от исследуемой случайной величины к случайной величине , распределенной равномерно в [0,1].

Случайная величина, равномерная в [0,1] , используется также при статистическом моделировании различных процессов, когда необходимо получать (моделировать) случайные величины с различными распределениями. Эти методы, иначе называемые методами Монте-Карло, в настоящее время широко используются как численные методы решения самых различных задач. В § 12 мы вернемся к этому вопросу.

2. Нормальное распределение занимает исключительно важное место в теоретических и прикладных вопросах теории вероятностей и математической статистики.

Определение. Распределение вероятностей, задаваемое плотностью

(7.16)

называется нормальным, а соответствующая случайная величина- нормальной случайной величиной с параметрами и и обозначается .

Смысл параметров и будет известен немного позже. Функция распределения случайной величины имеет вид

. (7.17)

При и распределение называется стандартным и обозначается ; для стандартного распределения плотность распределения и функция распределения представляются в виде:

(7.18)

(7.19)

Впервые мы познакомились с функциями (7.18) и (7.19) при изучении поведения биномиальных вероятностей при больших . Теперь мы можем перефразировать интегральную теорему Муавра-Лапласа следующим образом:

Случайная величина , где - число появления некоторого события при - независимых испытаниях Бернулли с вероятностью , распределена асимптотически нормально N(0,1), то есть

После Муавра (1733 г.) нормальное распределение независимо друг от друга было получено К.Гауссом (1809 г.) и П.Лапласом (1812 г.) в связи с их работами по теории ошибок измерений.

Рассмотрим некоторые свойства функции и .

Функция имеет максимум, равный , в точке ; точки перегиба . Нетрудно видеть, что ось абсцисс является асимптотой для при . Для дальнейшего понимания смысла параметра рассмотрим график функции при различных значениях :

Рис. 7.

Функция симметрична относительно прямой . На рис. 7 приведены графики функции для двух значений и при , причем . Мы видим, что чем меньше значение параметра , тем больше значение максимума у кривой . Поскольку согласно свойству 3) плотности вероятностей площадь под каждой из этих кривых равна 1, вероятность попадания в некоторый фиксированный интервал больше для той нормальной случайной величины, для которой величина параметра меньше. Таким образом, параметр является характеристикой разбросанности значений относительно параметра . При кривые на рис. 7 переместятся влево на величину и будут симметричны относительно оси ординат; при кривые рис. 7 переместятся влево на величину и будут симметричны относительно прямой .

Нормальное распределение вероятностей возникает каждый раз, когда мы имеем дело с непрерывной случайной величиной , которая формируется под воздействием очень большого числа независимых случайных факторов, влияние каждого из которых в отдельности мало и не превалирует среди остальных, а характер воздействия аддитивный. Последнее означает, что, если на величину оказывает воздействие случайный фактор , то получается величина где случайная «добавка» мала и равновероятна по знаку.

Широкое применение нормальное распределение имеет в медицине, технике, экономике, биологии и др. Кроме того, нормальное распределение имеет большое теоретическое значение, так как с его помощью получается ряд других распределений, используемых в математической статистике.

В практических приложениях часто бывают необходимы значения функций (7.16) и (7.17) при различных значениях и заданных и . Поскольку путем замены от нормальной случайной величины можно перейти к , то достаточно иметь таблицы значений функций (7.18) и (7.19).

3. Показательное (экспоненциальное) распределение

Случайная величина с функцией распределения

, (7.20)

называется экспоненциальной или показательной. Такие случайные величины характеризуют параметры различных социальных, физических, и производственных процессов, связанных с длительностью жизни индивидуума, функционирования сложной системы; время ожидания для выполнения заказа; расстояние между двумя последовательными взаимодействиями элементарных частиц между собой или со средой и др. Неотрицательная функция является характеристикой рассматриваемого процесса: интенсивность отказов элементов или коэффициенты смертности ( - возраст); в теории переноса излучений - характеризует рассеивающие и поглощающие свойства среды и называется коэффициентом ослабления ( - пространственная точка) и т. д.

Плотность распределения имеет вид

(7.21)

Приэкспоненциальный закон выражает, в частности, тот факт, что время безотказной работы (жизни) элемента на данном временном интервале не зависит от времени предшествующей работы , а зависит только от длины интервала . Такую случайную величину можно также рассматривать как случайную длительность промежутка между двумя последовательными пуассоновскими случайными величинами. В случае теории переноса излучений тот факт, что функция постоянна (не зависит от точки пространства), означает, что среда является однородной.

В случае функции (7.20), (7.21) принимают вид

, , (7.22)

. (7.23)

4. Распределение Парето.

Случайная величина с функцией распределения

, , (7.24)

называется распределенной по закону Парето. Такое распределение описывает вероятности в генеральной совокупности, из которой заранее убраны элементы с количественным признаком, меньшим, чем некоторый уровень .

Плотность распределения случайной величины Парето

, . (7.25)

5. Распределение Коши.

Случайная величина, определяемая двухпараметрической функцией распределения

, (7.26)

или плотностью распределения

, (7.27)

называется распределенной по закону Коши.

При и распределение (7.26) называется стандартным распределением Коши и обозначается . Функция распределения равна , так что параметры и , как и параметры и в нормальном распределении, имеют смысл: - параметр центра группирования, определяющий значение моды и медианы, - параметр масштаба. Распределение имеет широкое применение в технике, в частности, оно описывает распределение частиц, излучающихся радиоактивным источником.

7.4. Многомерные случайные величины

Рассмотренные до сих пор случайные величины были одномерными. Однако часто встречаются многомерные задачи, когда одновременно рассматриваются две или большее число случайных величин, определенных на одном и том же вероятностном пространстве.

Рассмотрим примеры.

Пример 1. Рассмотрим эксперимент, связанный с двукратным бросанием правильной игральной кости. Пусть - случайное число очков, выпавших первый раз, - второй раз. Тогда всевозможные пары выпавших подряд очков определяется системой случайных величин (.

Пример 2. В медицинских целях проводится обследование города по следующим признакам: возраст, рост, вес, пол.

Таким образом, отдельно взятый житель города будет характеризоваться четырьмя случайными величинами (.

Пример 3. Пусть - случайная величина, равномерно распределенная в интервале , т.е. - случайная точка интервала . Если же необходимо говорить о случайной точке на плоскости, скажем, равномерно распределенной в некоторой области, то, по – видимому, нужно будет говорить об объекте вида , где и координаты точки.

В известной задаче на геометрическую вероятность два лица договорились встретиться в интервале времени . Моменты их прихода ( и соответственно) случайны и образуют двумерную случайную величину .

Дадим формальное определение многомерной случайной величины.

Определение. Пусть F - произвольное вероятностное пространство и заданные на нем случайные величины, так, что каждому эти величины ставят в соответствие точку - мерного евклидова пространства . Отображение задаваемое случайными величинами , называется многомерной случайной величиной или случайным вектором.

Многомерная функция распределения

Обозначим функцию распределения случайной величины и , множество тех , для которых одновременно выполняются неравенства

, .

Так как события F, , то событие , как произведение этих событий, также принадлежит - алгебре F, т.е. можно говорить о вероятности .

Определение. Функция

, (7.28)

где - произвольная точка пространства , называется функцией распределения случайного вектора или функцией совместного распределения случайных величин (В дальнейшем индексы при будем опускать).

Величины часто удобно рассматривать как координаты точек пространства . Положение точки при этом случайно и функция выражает вероятность попадания этой точки в - мерной параллелепипед с ребрами параллельными осями координат.

Так, в случае двумерной случайной величины ( функция распределения есть вероятность попадания точки ( в область, заштрихованной на рис 8:

Рис. 8.

Зная функцию распределения, можно вычислить вероятность попадания точки ( в параллелепипед при произвольных числах и .

Так, в двумерном случае вероятность попадания случайной точки ( в прямоугольник определяется формулой (7.29), очевидность которой видна из рис. 9 и определения двумерного распределения :

(7.29)

Рис. 9.

Совместная функция распределения обладает следующими свойствами, доказательства которых аналогичны, как в одномерном случае.

2. – неубывающая функция по каждому аргументу,

3. - непрерывна слева по каждому аргументу,

4. , хотя бы при одном ,

5. , (7.30)

где ( - вектор размерности ().

Свойство (5) выражает тот факт, что по функции распределения – мерной случайной величины можно определить функцию распределения любой подсистемы случайных величин . Такие распределения называются маргинальными. В частности, функция распределения одномерной случайной величины

(7.31)

6. .

Докажем свойство 5 для случая . Пусть - некоторая возрастающая последовательность чисел, последовательность несовместимых событий. Событие эквивалентно событию . С другой стороны . Тогда согласно расширенной аксиоме сложения

т.е.

Дискретные и абсолютно непрерывные распределения

При решении конкретных задач чаще всего встречаются распределения следующих двух типов.

1. Дискретные распределения. Случайный вектор называется дискретным, если его координаты являются дискретными случайными величинами. Распределение такого вектора (дискретное распределение) можно задать с помощью набора вероятностей

где - значение случайной величины из множества допустимых значений , , ,…, и . В двумерном случае распределение можно представить в виде следующей таблицы.

Таблица 1.

	Значения с.в.
		…	…
Значения сл.вел.		…	…
		…	…

		…	…
			…
		…	…

Здесь Правый крайний столбец определяет распределение величины так как

Аналогичным образом нижняя последняя строка определяет распределение случайной величины .

Одним из примеров дискретного распределения является полиномиальное распределение. Оно является непосредственным обобщением распределения Бернулли на случай, когда каждое из независимых испытаний завершается одним из исходов . Обозначив - число испытаний, в которых появился исход , мы получим совокупность случайных величин , совместное распределение которых определяется формулой

, (7.32)

где . Название распределения связано с тем, что оно выражает общий член разложения полинома . Вывод формулы (7.32) аналогичен выводу формулы Бернулли.

Пример 4. В урне 3 белых, 5 черных и 2 красных шаров. Производится три последовательные извлечения шаров с возвращением. Случайный вектор задает число случаев появления соответственно белого, черного и красного шаров при трех извлечениях. Определить вероятность того, что белый шар появится один раз, черный 2 раза, а красный ни разу.

Решение. Используем формулу (7.32), где

2. Абсолютно непрерывные распределения. Распределение случайного вектора называется абсолютно непрерывным, если существует неотрицательная функция , что для любых значений аргументов выполняется равенство

(7.33)

где - совместная функция распределения вектора . Функция называется плотностью распределения случайного вектора . Она обладает следующими свойствами:

1. (условие нормировки),

2. В точках непрерывности функции имеет место равенство

3. Для любого множества

. (7.34)

4. По - мерной плотности можно определить плотность распределения любой подсистемы системы данных векторов

(7.35)

где

В частности, плотность распределения будет равна

. (7.36)

Доказательство этого свойства следует из свойств функции и ее определения.

Важнейшими абсолютно непрерывными распределениями являются равномерное и нормальное распределения.

Равномерное распределение. Случайный вектор называется равномерно распределенным в области , если вероятность попадания точки в любую её подобласть пропорциональна мере , а вероятность попадания этой точки в область является достоверным событием.

Плотность распределения определяется равенством

= (7.37)

где - мера области .

Нормальное распределение. Случайный вектор называется нормально распределенным, если её плотность распределения имеет вид

, (7.38)

где - вектор математических ожиданий (), - матрица, обратная ковариационной матрице , - ее определитель. В двумерном случае распределение (7.38) можно записать в виде

(7.39)

где - параметры распределения, смысл которых будет ясен из последующего изложения.

Независимость случайных величин.

Важнейшее понятие независимости событий сохраняет свое значение и для случайных величин. Если по многомерному распределению однозначно определяются одномерные распределения, то по одномерным распределениям многомерное распределение определяется в случае независимости случайных величин.

Определение. Два случайных вектора и со значениями в пространствах и соответственно, называются независимыми, если для любых множеств и события и независимы, т.е.

)=Р(). (7.40)

На основании данного определения можно записать условие независимости случайных векторов и в терминах функций распределения

, (7.41)

где - совместная функция распределения этих векторов, - распределения векторов и . Очевидность условия (7.41) следует из определения (7.40), если положить и , имея в виду .

Таким образом, условие независимости совокупности состоит в том, что их совместная функция распределения равна произведению одномерных распределений, т.е.

(7.42)

Верно и обратное утверждение: если функция распределения системы случайных величин имеет вид (7.42), где удовлетворяют условию

то эти величины независимы.

В конкретных дискретных и абсолютно непрерывных случаях условие независимости представляется в виде

(7.43)

- в дискретном случае и

(7.44)

где и - соответствующие плотности в непрерывном случае.

Пример 5. Пусть и независимы и имеют нормальные распределения и . Определить совместную плотность распределения этих величин.

Решение. Используем формулу (7.44).

Сравнивая полученный результат с формулой (7.39), мы видим, что параметры и - представляют математические ожидания, и - дисперсии случайных величин и , а параметр указывает на независимость этих случайных величин.

Теорема. Если и независимые случайные величины, то величины и также независимы.

Доказательство. Пусть и - два множества на прямой. Тогда в силу независимости и имеем следующую цепочку равенств

что и требовалось доказать.

Условные распределения. При рассмотрении зависимых событий было введено понятие условной вероятности события по формуле Байеса

, (7.45)

где - вероятность события А при условии, что событие В произошло. При рассмотрении зависимых случайных величин аналогичным понятием является понятие условного распределения случайной величины при условии В.

Пусть (,) двумерная случайная величина с плотностью распределения . Обозначим . Тогда условная функция распределения величины при условии согласно (7.45) равна

где - плотность распределения величины

Продифференцировав по , а затем устремив и использовав теорему о среднем значении интеграла на промежутке , мы получим функцию, называемую плотностью распределения при условии, что

, . (7.46)

Равенство (7.46) можно переписать и в виде

. (7.47)

Интегрируя равенство (7.47) по переменной , мы получим формулу

(7.48)

представляющую непрерывный аналог формулы полной вероятности. Аналогичные условные распределения справедливы и для дискретного случайного вектора (,), распределение которого задано в выше приведенной таблице 1.

При этом условное распределение вероятностей случайной величины при условии, что величина приняла значение определяется формулой

, .

Пример 6. Двумерная случайная величина (,) имеет распределение, указанное в следующей таблице 2

Таблица 2


	0,10	0,15
	0,15	0,25
	0,20	0,15

Определить: законы распределения и , а также условный закон распределения величины при условии, что =.

Решение.

Таким образом, мы получили распределение величины


р	0,45	0,55

Аналогично складывая вероятности по строкам таблицы, получим распределение


р	0,25	0,40	0,35

Условный закон распределения величины при условии, что =:

/	/	/
р	2/5	3/5

Функции от случайных величин

Во многих задачах теории вероятностей требуется определить вероятностное характеристики одной системы случайных величин по известным характеристикам другой системы, связанных с первой функциональной зависимостью.

Пусть на вероятностном пространстве F определена система из случайных величин (случайный вектор ) с совместной функцией распределения . Рассматривается новая совокупность случайных величин , связанная с предыдущей формулами

(), .

Задача заключается в определении функции распределения системы .

Общее решение задачи очевидно связано с трудностями вычислительного характера. Так, если вектор имеет плотность распределения , то функция распределения вектора определяется равенством

, (7.49)

где – область интегрирования, определяемая системой неравенств

Мы ограничимся системой двух случайных величин и двух функций (), (). Тогда

((. (7.50)

Решение задачи приведем для дискретных и непрерывных случайных величин.

Пусть - дискретная двумерная случайная величина с распределением , где - значения случайных величин и соответственно. Тогда распределения согласно (7.50) определяется по формуле

(7.51)

где - множество индексов , для которых выполняются неравенства

Если - непрерывный случайный вектор с плотностью распределения , то распределение согласно (7.50) определяется равенством

(7.51)

где .

Рассмотрим некоторые частные случаи.

1. Распределение суммы двух случайных величин. Пусть имеет плотность распределения . Найдем распределение суммы . Согласно (7.51) имеем

Расставив границу в двойном интеграле согласно рис. 10, получим

Рис. 10.

Продифференцировав по , найдем и плотность распределения суммы

. (7.52)

Часто суммируются независимые случайные величины, когда . Тогда плотность распределения суммы примет вид

(7.53)

Правая часть формулы (7.53) называется сверткой или композицией двух плотностей. Следовательно, плотность распределения суммы двух независимых случайных величин есть свертка плотностей и .

2. Плотность распределения частного. Найдем плотность распределения частного двух случайных величин по их совместной плотности распределения .

Согласно формуле (7.51) имеем

Расставим границы в двойном интеграле (см. рис. 11)

Взяв производную , мы получим плотность распределения частного:

Рис.11.

Упражнения к параграфу.

1. Пусть опыт состоит в двукратном подбрасывании игральной кости. Пространство элементарных событий состоит из всевозможных пар , где - количество очков, выпавших на 1-ой и 2-ой костях соответственно: . Составить ряд распределения случайной величины - суммы выпавших очков.

2. Игральную кость бросают до первого выпадения «шестерки». Описать пространство элементарных событий . Случайная величина - число бросаний. Найти ряд и функцию распределения.

3. Пусть производятся независимые испытания, в каждом из которых событие может появиться с одной и той же вероятностью . Испытания проводятся до первого «успеха» - появления события , но не более - раз. Описать случайную величину - число испытаний до первого успеха.

4. Из урны, содержащей 5 белых и черных шаров вытаскивается случайно 1 шар, фиксируют цвет и возвращают обратно. Найти , если известно, что при 6 - кратном повторении этого опыта математическое ожидание числа появления белого шара - равно 3.

5. Из урны, содержащей 6 белых и 3 черных шаров, случайным образом взяли 3 шара и переложили во вторую урну, в которой было 2 белых и 3 черных шара. Определить ряд распределения случайной величины - числа белых шаров во второй урне после этого.

6. В 1-ой урне было 2 белых и 4 черных шаров, во 2-ой 5 белых. Из 1-ой во 2-ю переложили случайно 3 шара, а затем из 2-ой таким же образом переложили 4 шара в 1-ую урну. Определить случайные величины и - число белых шаров соответственно в первой и второй урнах.

7. Из партии в N изделий, среди которых бракованных, выбрали для контроля штук. Определить - число бракованных изделий в выборке.

8. Из урны, содержащей 5 белых, 2 черных и 3 синих шара, производится выборка с возвращением объема 6 (вытаскивается 1 шар, отмечают цвет и возвращают обратно). Определить распределение случайной величины - числа появления белых шаров в выборке.

9. Случайные величины и независимы и распределены равномерно на [0,], . Найти плотность распределения .

10. Найти функцию и плотность распределения случайной величины , если известна .

11. Случайные величины независимы и одинаково распределены:

	-1	0	1
p

Найти математическое ожидание и дисперсию

12. Плотность распределения случайной величины

Найти постоянную .

13. Случайная величина имеет плотность вероятностей

Определить . Найти . Найти функцию и плотность распределения случайных величин и .

14. Пусть распределена равномерно в а равномерно в . Как распределен вектор случайных величин (,)?

Преобразование случайных величин.

15. Пусть случайная величина распределена нормально с параметрами и . Как распределена случайная величина

Найти плотность распределения вероятностей случайной величины

16. Пусть - функция распределения случайной величины . Как распределена случайная величина ? Случайная величина распределена равномерно в промежутке . Найти и случайных величин

=2 и =

17. Найти распределения случайных величин

где распределена по показательному закону с параметром

18. Случайная величина имеет распределение Коши

Найти плотность вероятностей и при .

19. Пусть и независимые дискретные случайные величины, принимающие одни и те же значения причем а . Вычислить .

20. Случайные величины и независимы и одинаково распределены

	0	1	…
			…

Найти распределение случайной величины

21. Задача Банаха. Некто носит всегда с собой 2 коробки спичек, Каждый раз, когда он хочет достать спичку, он выбирает наугад одну из коробок. Найти среднее число спичек, оставшихся в одной из коробок, в момент, когда другая окажется пустой. Считать, что в начале в каждой коробке было по N спичек, (см. В.Феллер т.1).

22. Пусть случайные величины независимы и одинаково распределены с функцией распределения

и .

Найти распределения и .

23. Решить предыдущую задачу, когда: 1) дискретно-равномерные случайные величины с вероятностями для ; 2) - равномерно распределены в промежутке

24. Каждая из случайных величин и имеют геометрическое распределение. Показать, что условное распределение при условии, что известна сумма + совпадает с дискретным распределением, т.е.

Биномиалъное распределение и распределение Пуассона.

25. Вероятность попадания в цель при каждом выстреле равна 0.7. Пусть сделано 20 выстрелов. Вычислить:

а) вероятность того, что будет хотя бы одно попадание;

б) вероятность того, что число попаданий не более трех;

в) наиболее вероятное число попаданий;

г) описать случайную величину - число попаданий.

26. Монета брошена 10 раз. Случайная величина , где и соответственно числа появления герба и цифры. Описать закон распределения .

27. Игральную кость бросают = 24 раза. Вычислить вероятность того, что:

а) каждая из сторон выпадет одинаковое число раз;

б) ни разу не выпадет шестерка;

в) описать случайную величину - число выпадений «шестерки».

28. Объем , который содержит молекул газа, разделен на ячеек. Вероятность попадания в любую ячейку одинакова для всех молекул. Найти вероятность того, что:

а) в первой ячейке содержатся , во второй - и т.д. в -ой ячейке - молекул;

б) в первой ячейке содержатся ровно молекул.

Какое распределение молекул в ячейках наиболее вероятно (будем считать, что , где - целое число)? Описать случайную величину - число молекул, попавших в – ю ячейку.

29. Пусть и - независимые случайные величины, распределенные по закону Пуассона с параметрами и . Показать, что =+ также имеет распределение Пуассона.

30. Пусть имеет распределение Пуассона с параметром . Показать, что вероятность принимает максимальное значение, если - наибольшее целое число, не превосходящее .

Контрольные вопросы

1. Какая величина называется случайной величиной?

2. Дайте определения дискретной и непрерывной случайных величин. Приведите примеры.

3. Что называется законом распределения случайной величиной?

4. Что называется рядом распределения дискретной случайной величиной?

5. Дайте определение функции распределения вероятности, перечислите свойства.

6. Дайте определение плотности распределения вероятностей, перечислите свойства.

7. Какая величин называется многомерной случайной величиной?

8. Дайте определение совместной функции распределения и совместной плотности распределения.

§ 8. Числовые характеристики случайных величин

Закон распределения (функция распределения или плотность распределения) полностью определяет случайную величину. Однако в теории вероятностей, и особенно, в ее приложениях, чтобы судить о случайной величине часто бывает достаточно знать некоторые средние величины, параметры, определяемые функцией распределения и отражающие наиболее важные особенности случайной величины. Такие параметры называются числовыми характеристиками случайных величин. К ним относятся математическое ожидание, дисперсия, моменты различных порядков и др.

Изложение этих понятий требует знания интегралов Стилтьеса и Лебега, полная теория которых дается в курсах математического анализа. Здесь мы приводим определения и основные свойства этих интегралов, необходимые нам в дальнейшем.

8.1. Интегралы

Определим сначала интеграл Лебега по вероятностной мере от простой функции.

Определение. Измеримая функция , заданная на множестве , называется простой, если это множество можно представить в виде суммы непересекающихся подмножеств

, Ø при ,

на каждом из которых функция принимает постоянное значение:

, если .

Примером простой функции является индикатор множества

Простую функцию можно представить в виде

Определение. Интегралом от простой функции по мере называется число

, (8.1)

если ряд в правой части сходится абсолютно.

Пусть теперь - произвольная измеримая функция. Имеет место

Теорема: Для любой измеримой функции существует последовательность простых функций, сходящаяся к равномерно.

Действительно, такую последовательность легко строить.

Пусть

Тогда последовательность простых функций

(8.2)

сходится равномерно к функции , так как

Определение. Интегралом Лебега от произвольной измеримой функции называется число

где - последовательность простых функций, сходящаяся к .

Используя последовательность (8.2), получим:

Интеграл Лебега совпадает с интегралом Римана, если подынтегральная функция непрерывна и под мерой понимается длина интервала разбиения области определения функции.

Теперь определим интеграл Стилтьеса. Пусть в интервале определены функции и ( - функция распределения). Разобьем интервал точками на конечное число частичных интервалов и образуем сумму

где - произвольная точка из .

Определение. Предел составленной суммы, не зависящий от способа разбиения интервала на части и выбора точек , при стремлении длины максимального из частичных интервалов к нулю называется интегралом Стилтьеса от функции с интегрирующей функцией и обозначается символом

Таким образом, .

Мы не остановимся на условиях существования и свойствах интеграла Стилтьеса, укажем лишь на то, что во всех случаях, когда интеграл Стилтьеса можно практически вычислить, он сводится либо к суммированию либо к вычислению интеграла Римана.

В частности,

Если , то .

Если - ступенчатая функция с разрывами в точках

, , , , то ,

( - величина скачка функции в точке ).

8.2. Математическое ожидание и его свойства

Математическое ожидание или среднее значение случайной величины является наиболее часто используемой числовой характеристикой. Его определение связано с обычным понятием о среднем значении.

Пусть имеется беспроигрышная лотерея, в которой имеется 500 выигрышей по 1000 рублей, 300 - по 10000 и 200 - по 50000 рублей. Требуется определить средний размер выигрыша на один билет. Решение здесь очевидно: надо общую сумму выигрышей разделить на количество билетов:

(руб.).

Перепишем это равенство в другом виде:

или

Введем теперь случайную величину - размер выигрыша на один билет. - дискретная случайная величина, принимающая значения 1000, 10000, 50000 с вероятностями 0,5; 0,3; 0,2 соответственно. Средний же размер выигрыша получается как сумма произведений значений нашей случайной величины на их вероятности.

Такого рода задачи на вычисление средних значений довольно часто возникают на практике. Чтобы иметь общий подход к их решению и вводится понятие математического ожидания или среднего значения случайной величины.

Определение. Если - дискретная случайная величина, имеющая ряд распределения

			….		…
			….		…

(8.3)

то ее математическим ожиданием называется число

(8.4)

при условии, что ряд справа абсолютно сходится.

Требование абсолютной сходимости ряда вызвано тем, что число (сумма ряда) должно оставаться неизменным при любой перестановке слагаемых в ряде, а таким свойством, как известно, обладают только абсолютно сходящиеся ряда.

Для непрерывных случайных величин с плотностью распределения естественный будет определение математического ожидания, как интеграла:

(8.5)

при условии, что интеграл .

Формулы (8.4) и (8.5) можно объединить, с помощью интеграла Стилтьеса. Для любой случайной величины с функцией распределения математическим ожиданием называется интеграл

(8.6)

Пользуясь определением интеграла Стилтьеса, можно дать также геометрическое истолкование понятию математического ожидания: оно равно разности площадей областей, заштрихованных на рис.12:

Рис. 12

Математическое ожидание как интеграл Лебега.

В теории вероятностей интеграл Лебега служит для выражения в едином виде всех форм математического ожидания.

Пусть (,F,) - вероятностное пространство и - дискретная случайная величина, принимающая значения ,… с вероятностями ,…. Тогда

Если - произвольная случайная величина, то по определению полагают, что

если последний интеграл существует.

Примеры вычисления математического ожидания:

Математическое ожидание случайной величины , распределенной по закону Пуассона

По формуле (8.4) имеем:

Математическое ожидание совпадает с параметром , определяющим распределение Пуассона.

Математическое ожидание случайной величины , распределенной по нормальному закону с плотностью распределения

По формуле (8.5) имеем:

После замены

Первый интеграл в правой части равен нулю, как интеграл от нечетной функции в симметричных пределах, а второй известен из математического анализа и равен .

В итоге получаем: , т.е. параметр , входящий в выражение для нормального закона, совпадает с математическим ожиданием случайной величины.

Пусть - случайная величина с равномерным распределением на отрезке . Ее плотность распределения

По формуле (8.5) .

Приведем основные свойства математического ожидания.

Свойство 1. Математическое ожидание постоянной величины равно самой постоянной:

, .

Действительно, постоянную величину можно рассматривать как случайную величину, которая принимает только одно значение с вероятностью единица.

Поэтому .

Свойство 2. Постоянный множитель можно вынести за знак математического ожидания

Доказательство следует из определения математического ожидания как суммы или интеграла, а постоянный множитель можно вынести за знак суммы или интеграла.

Свойство 3. Математическое ожидание алгебраической суммы (разности) случайных величин равно сумме (разности) их математических ожиданий.

Доказательство приведем для дискретных случайных величин. Пусть и заданы своими распределениями

			…
			…

(8.7)

			…
			…

По определению математического ожидания

где - совместное распределение случайных величин и .

По теореме о полной вероятности

, а .

Тогда

Следствие. Математические ожидание суммы конечного числа случайных величин равно сумме их математических ожиданий.

Свойство 4. Математическое ожидание произведения независимых случайных величин равно произведению их математических ожиданий

Доказательство. Пусть и - дискретные случайные величины, распределения которых приведены выше (8.7). В силу их независимости

Поэтому, .

Если и - независимые непрерывные случайные величины, то их совместная плотность распределения и

Следствие. Математическое ожидание произведения конечного числа независимых случайных величин равно произведению их математических ожиданий.

Математическое ожидание функции от случайной величины

Пусть требуется вычислить математическое ожидание случайной величины , где - случайная величина с известным законом распределения, - известная функция. Такую задачу можно решить, определив предварительно функцию распределения , а затем и . Но более простой способ решения дает следующая теорема, которую мы приводам без доказательства.

Теорема. Если - случайная величина, a , где - непрерывная функция, то

(8.8)

где , - плотность распределения .

Пример 1. Случайная величина имеет распределение Пуассона. Вычислить .

По формуле (8.8) получим

8.3. Дисперсия и ее свойства

Случайные величины могут иметь одинаковые математические ожидания, но существенно отличаться по характеру распределения. Так, случайные величины и с распределениями

	-0,01	0	0,01
	1/4	1/2	1/4

	-100	0	100
	1/4	1/2	1/4

имеют равные нулю математические ожидания. Отличие же их состоит в характере разброса принимаемых значений относительно своих математических ожиданий. (Значения случайной величины весьма близки к , значения же значительно удалены от ).

Во многих задачах именно разброс (рассеивание) значений случайной величины имеет большое значение. Для характеристики степени разброса значений случайной величины около ее математического ожидания вводится понятие дисперсии.

Определение. Дисперсией случайной величины называется число

, (8.9)

равное математическому ожиданию квадрата отклонения случайной величины от своего математического ожидания.

Раскрыв квадрат и воспользовавшись свойствами математического ожидания, формулу (8.9) можно представить и в другом виде

. (8.10)

Дисперсия имеет размерность квадрата случайной величины. Корень квадратный из дисперсии называется среднеквадратическим отклонением (стандартным отклонением) и обозначается : . На основании формулы (8.8) можно записать следующие выражения для вычисления дисперсии:

если - дискретная случайная величина, то

(8.11)

или

; (8.11^/)

если - непрерывная случайная величина, то

(8.12)

или

. (8.12^/)

Примеры вычисления дисперсии:

Найдем дисперсию случайной величины, распределенной по закону Пуассона

По формуле (8.11^/ ), учитывая, что (пример 1§8.1) имеем:

Для распределения Пуассона, таким образом,

2. Вычислим дисперсию случайной величины, распределенной по нормальному закону.

Так как , то по формуле (8.12) имеем:

(интегрируем по частям)

(первое слагаемое нулю).

Этим мы выяснили вероятностный смысл и второго параметра нормального закона распределения: параметр совпадает со среднеквадратическим отклонением случайной величины.

Перечислим основные свойства дисперсии.

Свойство 1. Дисперсия постоянной величины равна нулю

, .

Свойство 2. Постоянный множитель можно вынести за знак дисперсии, возведенная в квадрат

Свойство 3. Дисперсия алгебраической суммы независимых случайных величин равна сумме их дисперсий

Доказательство свойств 1 и 2 непосредственно следует из определения дисперсии. Докажем свойство 3:

так как величина в случае независимости и равна нулю:

(по свойству 2).

Пример использования свойств математического ожидания и дисперсии. Пусть случайная величина имеет биномиальное распределение вероятностей

, .

Вычислим и . - число «успехов» в испытаниях Бернулли. Очевидно, что можно представить в виде суммы слагаемых, , где - случайная величина, связанная с -ым испытанием и принимающая значения 0 или 1 с вероятностями , и соответственно,

, ,

тогда

8.4. Моменты случайной величины

Определение. Начальным моментом -го порядка случайной величины называется число , определяемое по формуле

Начальный момент первого порядка совпадает с математическим ожиданием .

Определение. Центральным моментом -го порядка называется число определяемый по формуле

Центральный момент второго порядка совпадает с дисперсией случайной величины: .

Существование момента -го порядка предполагает сходимость интеграла .

Теорема. Если случайная величина имеет момент -го порядка, то она имеет и моменты всех порядков, меньших чем .

Действительно, пусть . Тогда при и имеет место неравенство:

Первый интеграл в правой части неравенства конечен в силу конечности подынтегральной функции, а второй интеграл сходится в силу предположения. Следовательно существует момент -го порядка.

Между начальными и центральными моментами имеет место следующая связь:

В частности,

Моменты первых четырех порядков играют важную роль в математической статистике.

Так, центральный момент третьего порядка применяют для характеристики ассимметричности распределения.

Число называется коэффициентом ассимметрии.

Для симметричных распределений этот коэффициент равен нулю.

Центральный момент четвертого порядка применяют для характеристики островершинности распределения. Безразмерная величина