ГЛАВА 2. Стационарные случайные процессы

§1. Стационарность и эргодичность случайных процессов

В некоторых случаях часть параметров динамической системы на достаточно больших отрезках времени может принимать постоянные значения, не изменяться со времени. Статистические динамические системы могут обладать той или иной степенью стохастической стационарностью, постоянством. В частности, при исследовании, моделировании реальных процессов для упрощения полагают, что описывающие их случайные процессы обладают в необходимой мере стохастической стационарностью.

Случайный процесс называется строго стационарным или стационарным в узком смысле, если его конечномерные распределения инвариантны относительно сдвига по времени, т.е.

(1)

при любых ,

В случае строгой стационарности математическое ожидание и дисперсия постоянны, не зависят от времени, а ковариационная функция зависит лишь от разности аргументов:

, ,

(2)

Обратное заключение в общем случае не имеет место. Но в некоторых частных случаях, когда моментные функции первого и второго порядка определяют все конечномерные распределения, то из соотношений (2) будет следовать строгая стационарность .

Всегда интерес представляет расширение введенного понятия. Если ограничить условия стационарности равенствами (2), то класс случайных процессов, рассматриваемых как стационарные, существенно расширяется.

Случайный процесс называется стационарным в широком смысле, если ее математическое ожидание и дисперсия не зависят от времени , а ковариационная функция зависит лишь от разности аргументов.

Стационарные случайные процессы и y(t) называются взаимно стационарными в широком смысле, если выполняется равенство

при любых . (3)

Если x(t) стационарная в широком смысле дифференцируемая случайная функция и , то z()-также стационарная в широком смысле функция, причем

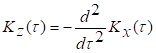(4)

Для дифференцируемости стационарной в широком смысле случайной функции необходимо и достаточно существование второй производной ковариационной функции при . Так как для стационарной в широком смысле случайной функции верно равенство

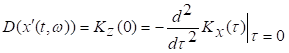, (5)

то условие дифференцируемости фактически равносильно условию конечности дисперсии производной от стационарной случайной функции.

Математическое ожидание и ковариационная функция являются основными характеристиками случайного процесса. Для их вычисления теоретически следует знать одномерное и двумерное распределения случайного процесса. Практически для их вычисления необходимо иметь множество реализации процесса, позволяющее вычислить оценки этих функций для различных значений аргумента. Методы получения таких оценок рассматриваются в математической статистике.

В некоторых случаях на практике нет возможности получать достаточное число таких реализаций. Часто в распоряжении исследователя имеется всего одна реализация процесса. Оказывается, при выполнении определенных условий и по одной такой единственной реализации можно вычислить моментные функции. В частности, одним из таких условий является эргодичность случайного процесса по его основным характеристикам.

Средним по конечному промежутку от реализации случайного процесса называется число, определяемое соотношением

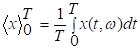. (6)

В приведенном определении подразумевается интегрируемость случайного процесса на указанном промежутке. В общем случае число является случайным.

Случайный процесс называется эргодическим относительно своего математического ожидания, если его математическое ожидание постоянно имеет место предельное соотношение

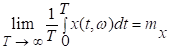. (7)

Равенство (7) означает, что при достаточно больших имеет место приближенная оценка

(8)

Следовательно, эргодичность случайного процесса по математическому ожиданию позволяет использовать в качестве оценки этого параметра процесса среднее значение для достаточно длинной реализации случайного процесса.

Имеет место следующий критерий эргодичности случайного процесса по его математическому ожиданию.

Теорема. Для того чтобы случайный процесс был эргодическим по его математическому ожиданию, необходимо и достаточно существование предела

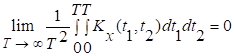(9)

Для эргодичности случайного процесса по его математическому ожиданию достаточно выполнение условия

(10)

Необходимым и достаточным условием для эргодичности относительно математического ожидания стационарного процесса является условие

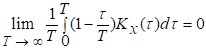(11)

которое непосредственно следует из (9).

Точно также из (10) следует, что в случае стационарности случайного процесса условие

(12)

является достаточным для эргодичности по математическому ожиданию.

Понятие эргодичности по математическому ожиданию естественным образом обобщается на эргодичность по дисперсии или по ковариационной функции. Если есть исходный случайный процесс, то положим, как принято, .

Случайный процесс называется эргодическим по дисперсии, если дисперсия постоянна и справедливо равенство

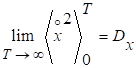
Стационарный случайный процесс называется эргодическим по ковариационной функции, если выполняется условие

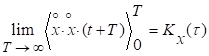
Стационарные случайные процессы могут обладать или не обладать эргодическим свойством. Эргодическое свойство состоит в том, что любая реализация эргодического стационарного случайного процесса достаточной продолжительности характеризует всю совокупность реализаций процесса. Иными словами, любая реализация эргодического процесса с конечным числом состояний рано или поздно пройдет через любое состояние независимо ото того , в каком состоянии находится этот процесс в начальный момент времени.

Задача1. Является ли пуассоновский процесс с параметром стационарным в широком смысле?

Решение. Пуассоновский процесс с параметром задается вероятностями

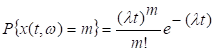, m=0,1,... .

нетрудно убедиться, что = t, = t и процесс не стационарен. Можно также убедиться, что

.

Задача2. Пусть-случайная величина с плотностью распределения f(x)=cosx, и α,𝜈-постоянные. Построим случайный процесс x(t)=αsin(𝜈t+).

а) Будет ли этот процесс стационарным?

б) Можно ли, пользуясь одной реализацией этого процесса, на достаточно большом промежутке времени оценить его математическое ожидание?

Решение. Если есть плотность распределения случайной величины и =F[], то

.

Поэтому .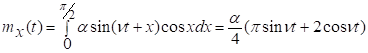

Аналогично

,

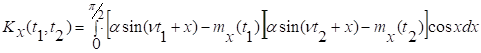откуда

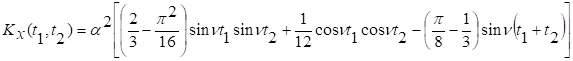
Следовательно,

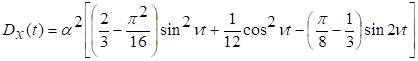
Процесс очевидным образом не стационарен.

б) Всякая реализация процесса будет синусоидой с некоторой постоянной начальной фазой

Очевидным образом 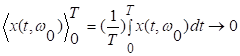при , т.е. среднее по времени любой реализации не сходится к математическому ожиданию с увеличением промежутка времени . Поэтому оценить нельзя.

Задача3. Пусть -случайная величина, равномерно определенная на отрезке [0;2], α и 𝜈-постоянные. Доказать, что случайный процесс x(t)=αsin(𝜈t+) стационарный в широком смысле и эргодический по математическому ожиданию и ковариационной функции.

Решение. Плотность случайной величины есть функция

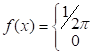
Поэтому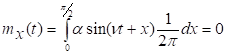

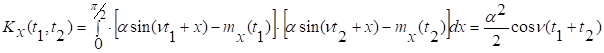
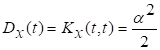. Процесс стационарен.

Выясним теперь вопрос эргодичности случайного процесса. Легко проверить, что выполняется необходимое и достаточное условие эргодичности по математическому ожиданию. Действительно ,

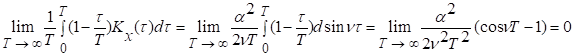
Следовательно, эргодичность случайного процесса то математического ожидания имеет место:

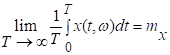. Поскольку в рассматриваемом случае , то и потому

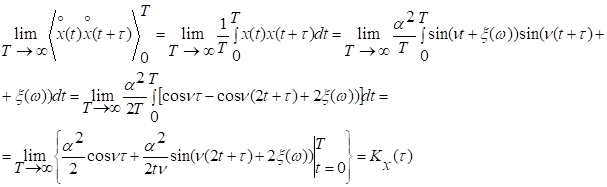Поэтому процесс эргодичен и по ковариационной функции.

Задача 4. Дан случайный процесс , где α и -положительные постоянные, -нормальная случайная величина и . Будет ли стационарным процессом? Найти математическое ожидание, ковариационную функцию и дисперсию .

Решение. При решении задачи воспользуемся следующим фактом. Если есть случайная величина с плотностью распределения , а то

(13)

Следовательно, согласно (13) имеем:

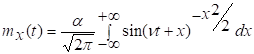
Для вычисления введем функцию

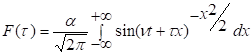
Нетрудно установить, что

,

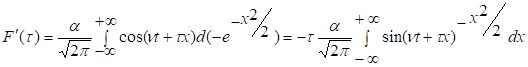т.е. .

Отсюда имеем, что 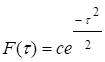, c=const.

Так как =αsin𝜈t, то c=αsin𝜈t и

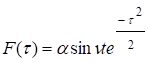
С другой стороны, , следовательно,

.

Определим теперь ковариационную функцию. Поскольку то

откуда

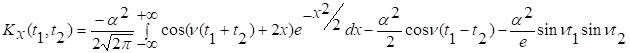
Рассмотрим функцию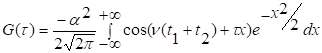

Как и в случае математического ожидания можно показать, что имеет место дифференциальное уравнение.

,

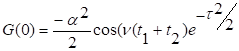
Так как

Полученное выражение для ковариационной функции можно записать в следующем виде:

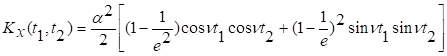
Дисперсия процесса равна

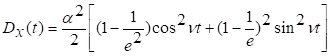
Процесс очевидным образом нестационарен.

Задача 5. Случайный процесс представляет собой случайный гармоническое колебание , где >0-случайная амплитуда с конечным начальным моментом второго порядка M, -независимая от случайная фаза колебания, равномерно распределенная на отрезке . Является ли данный процесс стационарным в широком смысле и эргодическим относительно математического ожидания?

Решение. Представим случайный процесс в виде

Введем обозначения ,

Так как и независимы, то

.

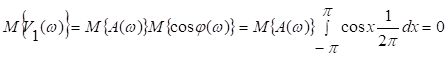Точно также . Следовательно,

в любой момент времени .

Найдем теперь ковариационную функцию процесса. Так как , то и потому

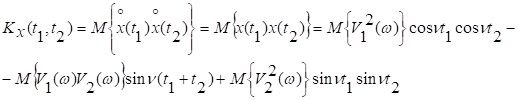
Заметим, что 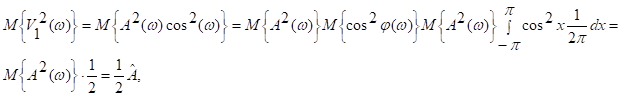где есть среднее значение квадрата случайной амплитуды .

Точно также , .

Следовательно, .

Дисперсия процесса .

По определению случайный процесс является стационарным в широком смысле.

Рассмотрим теперь вопрос эргодичности процесса по математическому ожиданию. Вычислим среднее по конечному промежутку времени от одной произвольной реализации :

Математическое ожидание постоянно, и .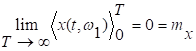

Поэтому процесс эргодический относительно математического ожидания.

Задача 6. Случайный процесс представляет собой случайную телеграфную волну, возникающую следующим образом. На оси o имеется простейший поток событий с интенсивностью . Случайный процесс попеременно принимает значения +α и -α. При наступлении очередного события в простейшем потоке случайный процесс скачком меняет свое состояние с +α на -α или наоборот. Является ли данный процесс стационарным, эргодическим по математическому ожиданию?

Решение. Динамику эволюцию случайного процесса можно изобразить следующим графиком:

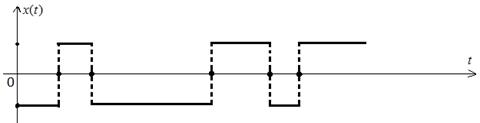
Поскольку моменты знака абсолютно не связаны со значениями случайного процесса , то нет никаких оснований считать какое-либо из значений +α, -α вероятнее другого. Следовательно, одномерный закон распределения случайного процесса имеет вид : , .

Вычислим математическое ожидание и дисперсию процесса:

,

.

Найдем теперь ковариационную функцию процесса . Так как по условию задачи задан простейший поток событий интенсивности , то вероятность появления m событий за время равна.

.

По определению

,

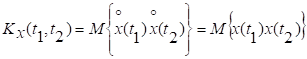поэтому нам необходимо найти математическое ожидание произведения двух сечений процесса и .

Если в интервале , за время произойдет четное число событий , то , ибо произойдет четное число перемен знака :

, .

Если же в интервале произойдет нечетное число событий , то и поэтому

, , .

Значит,

.

Вычислим вероятности из последнего соотношения. Ясно ,что

, .

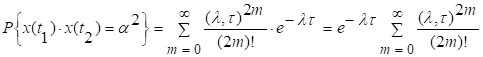Следовательно,

.

Итак, при имеем следующее представление для ковариационной функции:

,

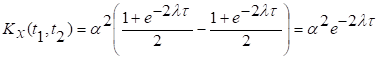т.е. ,

Поскольку ковариационная функция симметрична по своим аргументам, , то при точно также имеем , .

Объединяя полученные формулы, окончательно имеем

, .

Случайный процесс стационарен, поскольку , постоянны и ковариационная функция зависит лишь от разности аргументов. Поскольку при , то имеет место и эргодичность процесса.

1. Является ли случайный процесс стационарным в широком смысле, если -стационарный случайный процесс, а -случайная величина, не связанная с ?

2. Известна ковариационная функция стационарного случайного процесса . Найти среднее значение квадрата приращения процесса за время .

3. Пусть процесс Пуассона с параметром , а . Будет ли этот процесс эргодичен относительно своего математического ожидания?

4. Случайный процесс задан уравнением, , где и -независимые случайные величины, принимающие с равной вероятностью +1 и -1. Будет ли этот процесс стационарен в широком смысле и эргодичен относительно математического ожидания?

5. Случайный процесс задан каноническим разложением 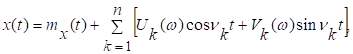где и -центрированные некоррелированные случайные величины с , для всех Показать, что данный процесс является стационарным в широком смысле. Будет ли этот процесс эргодичен по математическому ожиданию?