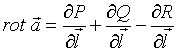№Автор= Эмирова
И.С.
№дисциплина= Математический
анализ(1к., Физ Фак)
Блок 1
№Модуль1=Дифференциальное исчисление функции одной переменной
№Тема=Действительные
числа и их последовательности
№Вопрос1
Числовая
последовательность ![]() называется бесконечно
большой последовательностью (б.б.)
и пишут
называется бесконечно
большой последовательностью (б.б.)
и пишут ![]() , если
, если ![]()
![]()
![]() …
…
№да
![]()
№нет
![]()
№нет
![]()
№нет
![]()
№Вопрос2
Бесконечно малой (б.м.) последовательностью является…
№да
Сумма двух б.м. последовательностей
№да
Произведение
ограниченной последовательности на б.м.
последовательность
№нет
Частное двух б.м. последовательностей
№нет
Произведение
неограниченной последовательности на б.м. последовательность
№Вопрос2
Бесконечно малой (б.м.) последовательностью является…
№да
Произведение двух б.м. последовательностей
№да
Произведение
любого числа б.м.
последовательностей
№нет
Частное двух б.м. последовательностей
№нет
Произведение
неограниченной последовательности на б.м. последовательность
№Вопрос1
Числовая последовательность ![]() называется
сходящейся, если она имеет предел
называется
сходящейся, если она имеет предел
№да
конечный
№нет
бесконечный
№нет
1
№нет
№Вопрос1
Числовое множество ![]() называется
ограниченным сверху, если
называется
ограниченным сверху, если ![]() число
число ![]() такое, что
такое, что ![]()
![]() …
…
№да
![]()
№нет
![]()
№нет
![]()
№нет
![]()
№Вопрос1
Числовое множество ![]() называется
ограниченным снизу, если
называется
ограниченным снизу, если ![]() число
число ![]() такое, что
такое, что ![]()
![]() …
…
№да
![]()
№нет
![]()
№нет
![]()
№нет
![]()
№Вопрос1
Точной верхней гранью
множества ![]() или супремумом
или супремумом ![]() называется…
называется…
№да
наименьшая среди верхних
границ множества ![]()
№нет
наибольшая среди верхних
границ множества ![]()
№нет
наименьшая среди нижних
границ множества ![]()
№нет
наибольшая среди нижних
границ множества ![]()
№Вопрос1
Точной нижней гранью
множества ![]() или инфимумом
или инфимумом ![]() называется…
называется…
№да
наибольшая среди нижних
границ множества ![]()
№нет
наибольшая среди верхних
границ множества ![]()
№нет
наименьшая среди нижних
границ множества ![]()
№нет
наименьшая среди верхних
границ множества ![]()
№Вопрос1
Множество ![]() называется
ограниченным множеством, если оно…
называется
ограниченным множеством, если оно…
№да
ограничено и сверху и снизу
№нет
ограничено
только снизу
№нет
ограничено только
сверху
№нет
неограничено
№Вопрос1
Множество ![]() называется
неограниченным множеством, если оно…
называется
неограниченным множеством, если оно…
№да
неограничено хотя бы с одной стороны
№нет
ограничено
только снизу
№нет
ограничено только
сверху
№нет
ограничено
сверху и снизу
№Вопрос1
Последовательность ![]() называется
ограниченной сверху, если существует такое число
называется
ограниченной сверху, если существует такое число ![]() ,что каждый элемент
,что каждый элемент
![]() последовательности
последовательности ![]() удовлетворяет
неравенству…
удовлетворяет
неравенству…
№да
![]()
№нет
![]()
№нет
![]()
![]()
№нет
![]()
№Вопрос1
Последовательность ![]() называется
ограниченной снизу, если существует такое число
называется
ограниченной снизу, если существует такое число ![]() , что каждый элемент
, что каждый элемент ![]() последовательности
последовательности ![]() удовлетворяет
неравенству…
удовлетворяет
неравенству…
№да
![]()
№нет
![]()
№нет
![]()
№нет
![]()
№Вопрос1
Последовательность ![]() называется
неограниченной, если для любого положительного числа
называется
неограниченной, если для любого положительного числа ![]() найдется элемент
найдется элемент ![]() этой последовательности,
удовлетворяющий неравенству…
этой последовательности,
удовлетворяющий неравенству…
№да
![]()
№нет
![]()
№нет
![]()
№нет
![]()
№Вопрос1
Последовательность
называется бесконечно малой последовательностью
(б.м.), если предел последовательности равен…
№да
0
№нет
1
№нет
-1
№нет
![]()
0
№Вопрос1
Числовая последовательность ![]() называется
расходящейся, если она имеет предел
….
называется
расходящейся, если она имеет предел
….
№да
бесконечный
№нет
конечный
№нет
1
№нет
0
№Вопрос2
Если
последовательность ![]() сходящаяся, то она ….
сходящаяся, то она ….
№да
имеет единственный предел
№да
ограничена
№нет
имеет два предела
№нет
не
имеет предела
№Вопрос1
Монотонные последовательности
ограничены ….
№да
либо сверху, либо снизу
№нет
сверху
№нет
снизу
№нет
и сверху и снизу
№Вопрос1
Для сходимости монотонной
последовательности н. и д., чтоб она была….
№да
ограничена
№нет
не ограничена
№нет
конечна
№нет
бесконечна
№Вопрос1
Из любой ограниченной
последовательности можно выделить ….
№да
сходящуюся подпоследовательность
№нет
ограниченную подпоследовательность
№нет
расходящуюся подпоследовательность
№нет
конечную подпоследовательность
№Тема=Предел и непрерывность функции одной переменной
№Вопрос2
Функцию можно задать следующим способом…
№да
графическим
№да
табличным
№нет
подстановки
№нет
сложения
№Вопрос1
Первый замечательный предел имеет вид…
№да
![]()
№нет
![]()
№нет
![]()
№нет
![]()
№Вопрос2
Второй замечательный предел имеет вид…
№да
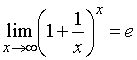
№да
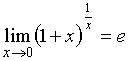
№нет
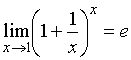
№нет
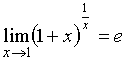
№Вопрос
Для существования предела функции н. и д., чтобы
выполнялись условия …
№да
односторонние пределы должны быть равны друг другу
№нет
существовали конечные пределы
№нет
существовали бесконечные пределы
№нет
существовали односторонние пределы
№Вопрос1
Функция ![]() называется неубывающей
на множестве
называется неубывающей
на множестве ![]() , если для
, если для ![]() …
…
№да
![]()
№нет
![]()
№нет
![]()
№нет
![]()
№Вопрос1
Функция ![]() называется
невозрастающей на множестве
называется
невозрастающей на множестве ![]() , если для
, если для ![]() …
…
№да
![]()
№нет
![]()
№нет
![]()
№нет
![]()
№Вопрос1
Пусть ![]() - точка разрыва
функции
- точка разрыва
функции ![]() . Она называется
точкой разрыва I рода, если...
. Она называется
точкой разрыва I рода, если...
№да
существуют конечные односторонние пределы слева и
справа ![]() и
и ![]()
№нет
существуют бесконечные односторонние пределы слева и
справа ![]() и
и ![]()
№нет
существует предел слева ![]()
№нет
существует предел справа ![]()
№Вопрос2
Пусть ![]() - точка разрыва
функции
- точка разрыва
функции ![]() . Она называется
точкой разрыва II рода, если...
. Она называется
точкой разрыва II рода, если...
№да
хотя бы один
односторонний предел равен ![]() или не существует
или не существует
№да
оба
односторонних предела равны ![]()
№нет
существует предел слева ![]()
№нет
существует предел справа ![]()
№Вопрос1
Точка ![]() , являющаяся точкой разрыва I рода,
называется точкой устранимого разрыва, если...
, являющаяся точкой разрыва I рода,
называется точкой устранимого разрыва, если...
№да
выполняются условие ![]()
![]()
№нет
выполняются условие ![]()
![]()
№нет
существует предел слева ![]()
№нет
существует предел справа ![]()
№Вопрос1
Точка ![]() , являющаяся точкой разрыва II рода,
называется точкой бесконечного разрыва, если ...
, являющаяся точкой разрыва II рода,
называется точкой бесконечного разрыва, если ...
№да
хотя бы один из односторонних пределов равен бесконечности
№нет
хотя бы один из односторонних пределов конечен
№нет
оба односторонних
предела конечны
№нет существует предел справа ![]()
№Вопрос1
Пусть даны два множества ![]() и
и ![]() , то функцией называется такое соответствие, когда….
, то функцией называется такое соответствие, когда….
№да
Каждому
элементу ![]() соответствует
определенный элемент
соответствует
определенный элемент ![]()
№нет
Некоторым
элементам ![]() соответствуют
определенные элементы
соответствуют
определенные элементы ![]()
№нет
Каждому
элементу ![]() соответствует
несколько элементов
соответствует
несколько элементов ![]()
№нет
Каждому
элементу ![]() соответствует два
элемента
соответствует два
элемента ![]()
№Вопрос1
Графики прямой и обратной
функции симметричны относительно
№да
Прямой ![]()
№нет
Оси Ox
№нет
Оси Oy
№нет
Начала
координат
№Вопрос1
Функция ![]() называется четной,
если для любого
называется четной,
если для любого ![]() из ее области
определения ….
из ее области
определения ….
№да
![]()
№нет
![]()
№нет
![]()
№нет
![]()
№Вопрос1
Функция ![]() называется нечетной,
если для любого
называется нечетной,
если для любого ![]() из ее области
определения ….
из ее области
определения ….
№да
![]()
№нет
![]()
№нет
![]()
№нет
![]()
№Вопрос1
График четной функции симметричен относительно….
№да
Оси ![]()
№нет
Оси ![]()
№нет
Нет
симметрии
№нет
Начала
координат
№Вопрос1
График нечетной функции симметричен относительно….
№да
Начала
координат
№нет
Оси ![]()
№нет
Нет
симметрии
№нет
Оси ![]()
№Тема=Производная и дифференциал функции одной переменной
№Вопрос2
Производная ![]() определяет….
определяет….
№да
Мгновенную
скорость материальной точки в момент
времени ![]()
№да
Силу
тока, проходящего через поперечное сечение проводника, за время ![]()
№нет
Координату материальной точки
№нет
Мгновенное
ускорение материальной точки в момент времени ![]()
№Вопрос2
Производная ![]() определяет….
определяет….
№да
Мгновенную
скорость материальной точки в момент
времени ![]()
№да
Теплоемкость
тела, при данной температуре ![]()
№нет
Координату материальной точки
№нет
Мгновенное
ускорение материальной точки в момент времени ![]()
№Вопрос2
Производная ![]() определяет….
определяет….
№да
Теплоемкость
при данной температуре ![]()
№да
Силу
тока, проходящего через поперечное сечение проводника, за время ![]()
№нет
Координату материальной точки
№нет
Мгновенное
ускорение материальной точки в момент времени ![]()
№Вопрос2
Производная ![]() равна….
равна….
№да
Угловому
коэффициенту касательной в точке ![]() к графику функции
к графику функции ![]()
№да
Тангенсу
угла наклона касательной в точке ![]() к графику функции
к графику функции ![]()
с
положительным направлением оси ![]()
№нет
синусу
угла наклона касательной в точке ![]() к графику функции
к графику функции ![]()
с
положительным направлением оси ![]()
№нет
тангенсу
угла наклона касательной в точке ![]() к графику функции
к графику функции ![]()
№Вопрос4
Установить соответствие между
функциями и их производными
1)![]()
2)![]()
3)![]()
4)![]()
№да
![]()
№да
![]()
№да
![]()
№да
![]()
№Вопрос1
Производной степенной функции
![]() является функция…
является функция…
№да
![]()
№нет
![]()
№нет
![]()
№нет
![]()
№Вопрос1
Производной показательной
функции ![]() является функция…
является функция…
№да
![]()
№нет
![]()
№нет
![]()
№нет
![]()
№Вопрос1
Производной экспоненциальной
функции ![]() является функция…
является функция…
№да
![]()
№нет
![]()
№нет
![]()
№нет
![]()
№Вопрос1
Производной функции ![]() является …
является …
№да
![]()
№нет
![]()
№нет
![]()
№нет
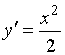
№Вопрос1
Производной ![]() является …
является …
№да
![]()
№нет
![]()
№нет
![]()
№нет
![]()
№Вопрос1
Производной функции ![]() является функция…
является функция…
№да
![]()
№нет
![]()
№нет
![]()
№нет
![]()
№Вопрос4
Установить соответствие между
функциями и их производными
1)![]()
2)![]()
3)![]()
4)![]()
№да
![]()
№да
![]()
№да
![]()
№да
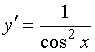
№Вопрос1
Производной функции ![]() является функция…
является функция…
№да
![]()
№нет
![]()
№нет
![]()
№нет
![]()
№Вопрос1
Производной функции ![]() является функция…
является функция…
№да
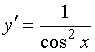
№нет
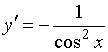
№нет
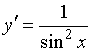
№нет
![]()
№Вопрос4
Установить соответствие между
функциями и их производными
1)![]()
2)![]()
3)![]()
4)![]()
№да
![]()
№да
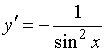
№да
![]()
№да
![]()
№Вопрос1
Производной функции ![]() является функция…
является функция…
№да
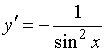
№нет
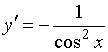
№нет
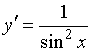
№нет
![]()
№Вопрос1
Производной функции ![]() является функция…
является функция…
№да
![]()
№нет
![]()
№нет
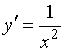
№нет
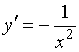
№Вопрос1
Производной функции ![]() является функция…
является функция…
№да
![]()
№нет
![]()
№нет
![]()
№нет
![]()
№Вопрос4
Установить соответствие между
функциями и их производными
1)![]()
2)![]()
3)![]()
4)![]()
№да
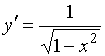
№да
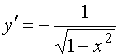
№да
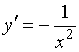
№да
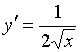
№Вопрос1
Производной функции ![]() является функция…
является функция…
№да
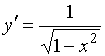
№нет
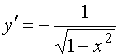
№нет
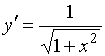
№нет
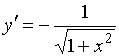
№Вопрос1
Производной функции ![]() является функция…
является функция…
№да
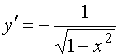
№нет
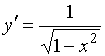
№нет
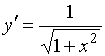
№нет
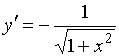
№Вопрос1
Производной функции ![]() является функция…
является функция…
№да
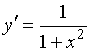
№нет
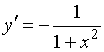
№нет
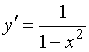
№нет
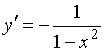
№Вопрос1
Производной функции ![]() является функция…
является функция…
№да
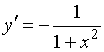
№нет
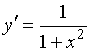
№нет
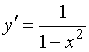
№нет
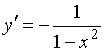
№Вопрос1
Производной функции ![]() является функция…
является функция…
№да
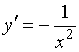
№нет
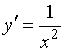
№нет
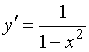
№нет
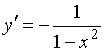
№Вопрос1
Производной функции ![]() является функция…
является функция…
№да
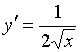
№нет
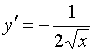
№нет
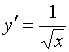
№нет
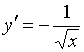
№Вопрос4
Установить соответствие между
функциями и их производными
1)![]()
2)![]()
3)![]()
4)![]()
№да
![]()
№да
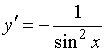
№да
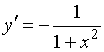
№да
![]()
№Вопрос1
Производной функции ![]() является функция…
является функция…
№да
![]()
№нет
![]()
№нет
![]()
№нет
![]()
№Вопрос1
Производной функции ![]() является функция…
является функция…
№да
![]()
№нет
![]()
№нет
![]()
№нет
![]()
№Вопрос2
Если каждая из функций ![]() и
и ![]() дифференцируема в
точке
дифференцируема в
точке ![]() , то имеют место формулы…
, то имеют место формулы…
№да
![]()
№да
![]()
№нет
![]()
№нет
![]()
№Вопрос1
Если функция ![]() дифференцируема в
точке
дифференцируема в
точке ![]() и
и ![]() - множитель, то имеет место формула…
- множитель, то имеет место формула…
№да
![]()
№нет
![]()
№нет
![]()
№нет
![]()
№Вопрос1
Если каждая из функций ![]() и
и ![]() дифференцируема в
точке
дифференцируема в
точке ![]() , то имеет место формула…
, то имеет место формула…
№да
![]()
№нет
![]()
№нет
![]()
№нет
![]()
№Вопрос1
Если каждая из функций ![]() и
и ![]() дифференцируема в
точке
дифференцируема в
точке ![]() , то имеет место формула…
, то имеет место формула…
№да
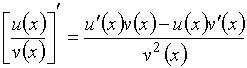
№нет
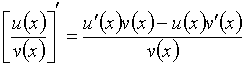
№нет
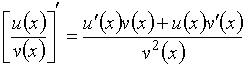
№нет
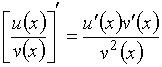
№Вопрос1
Для того,
чтобы график функции ![]() имел при
имел при ![]() горизонтальную
асимптоту, н. и д., чтобы существовали
два предельных значения
горизонтальную
асимптоту, н. и д., чтобы существовали
два предельных значения
№да
![]() и
и ![]()
№нет
![]() и
и ![]()
№нет
![]() и
и ![]()
№нет
![]() и
и ![]()
№Вопрос1
Пусть даны функции ![]() и
и ![]() параметра
параметра ![]() . Тогда первую производную можно найти по формуле
. Тогда первую производную можно найти по формуле
№да

№нет
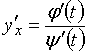
№нет
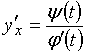
№нет
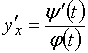
№Тема=Производные высших порядков
№Вопрос2
Правильное утверждение….
№да
Если ![]() ,
, ![]() , то
, то ![]()
№да
Если ![]() ,
, ![]() меняет знак в точке
меняет знак в точке ![]() с
+ на —, то
с
+ на —, то ![]()
№нет
Если ![]() ,
, ![]() , то
, то ![]()
№нет
Если ![]() ,
, ![]() , то
, то ![]()
№Вопрос2
Правильное утверждение….
№да
Если ![]() ,
, ![]() , то
, то ![]()
№да
Если ![]() ,
, ![]() меняет знак в точке
меняет знак в точке ![]() с
— на +, то
с
— на +, то ![]()
№нет
Если ![]() ,
, ![]() , то
, то ![]()
№нет
Если ![]() ,
, ![]() , то
, то ![]()
№Вопрос2
Правильное утверждение….
№да
Если ![]() ,
, ![]() , то
, то ![]()
№да
Если ![]() ,
, ![]() , то
, то ![]()
№нет
Если ![]() ,
, ![]() , то
, то ![]()
№нет
Если ![]() ,
, ![]() , то
, то ![]()
№Вопрос2
Правильное утверждение….
№да
Если ![]() на
на ![]() , то
, то ![]() вогнута
на
вогнута
на ![]()
№да
Если ![]() на
на ![]() , то
, то ![]() выпукла
на
выпукла
на ![]()
№нет
Если ![]() на
на ![]() , то
, то ![]() выпукла
на
выпукла
на ![]()
№нет
Если ![]() на
на ![]() , то
, то ![]() вогнута на
вогнута на ![]()
№Вопрос2
Правильное утверждение….
№да
Если ![]() на
на ![]() , то
, то ![]() вогнута
на
вогнута
на ![]()
№да
Если ![]() на
на ![]() , то
, то ![]() выпукла
на
выпукла
на ![]()
№нет
Если ![]() на
на ![]() , то
, то ![]() выпукла
на
выпукла
на ![]()
№нет
Если ![]() на
на ![]() , то
, то ![]() вогнута
на
вогнута
на ![]()
№Вопрос1
Прямая ![]() является вертикальной
асимптотой функции
является вертикальной
асимптотой функции ![]() , если …
, если …
№да
Хотя
бы один из ![]() или
или ![]() равен
равен ![]() или
или ![]()
№нет
Оба
предела ![]() или
или ![]() равны
равны ![]()
№нет
Оба
предела ![]() или
или ![]() равны
равны ![]()
№нет
![]() или
или ![]()
№Вопрос1
Для того,
чтобы график функции ![]() имел при
имел при ![]() наклонную
асимптоту
наклонную
асимптоту ![]() , н. и д., чтобы существовали
два предельных значения
, н. и д., чтобы существовали
два предельных значения
№да
![]() и
и ![]()
№нет
![]() и
и ![]()
№нет
![]() и
и ![]()
№нет
![]() и
и ![]()
№Модуль2=Дифференциальное исчисление функций многих переменных
№Тема=Предел
и непрерывность функций многих переменных
№Вопрос2
Если функция ![]() непрерывна на
некотором замкнутом ограниченном множестве
непрерывна на
некотором замкнутом ограниченном множестве
![]() , то…
, то…
№да
она
ограничена на этом множестве
№да
она достигает на этом множестве своих точных верхней и нижней граней
№нет
она
строго монотонна на этом множестве
№нет
она
не ограничена на этом множестве
№Вопрос2
Если функция ![]() непрерывна на
некотором замкнутом ограниченном множестве
непрерывна на
некотором замкнутом ограниченном множестве
![]() , то…
, то…
№да
она
ограничена на этом множестве
№да
равномерно непрерывна
на этом множестве
№нет
она
строго монотонна на этом множестве
№нет
она
не ограничена на этом множестве
№Вопрос2
Если функция ![]() непрерывна на
некотором замкнутом ограниченном множестве
непрерывна на
некотором замкнутом ограниченном множестве
![]() , то…
, то…
№да
она
достигает на этом множестве своих точных верхней и нижней граней №да
равномерно непрерывна
на этом множестве
№нет
она
строго монотонна на этом множестве
№нет
она
не ограничена на этом множестве
№Вопрос1
Функция
![]() дифференцируема
в точке
дифференцируема
в точке ![]() ,если существуют
,если существуют ![]() ,
, ![]() в некоторой
окрестности точки
в некоторой
окрестности точки ![]() и
и![]() ,
, ![]() ...
...
№да
непрерывны
в точке ![]()
№нет
дифференцируемы в точке ![]()
№нет
равномерно
непрерывны в окрестности точки ![]()
№нет
непрерывны
в окрестности точки ![]()
№Тема=Частные
производные и дифференциалы
№Вопрос1
Достаточным
условием дифференцируемости сложной функции ![]() в точке
в точке ![]() является…
является…
№да
дифференцируемость
внешней функции ![]() в точке
в точке ![]() , внутренних функций
, внутренних функций  в точке
в точке ![]() и выполнение
равенств
и выполнение
равенств 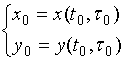
№нет
дифференцируемость
внешней функции ![]() в точке
в точке ![]()
№нет
дифференцируемость
внутренних функций  в точке
в точке ![]()
№нет
непрерывность
внешней функции ![]() в точке
в точке ![]()
№Вопрос1
Если
сложная функция ![]() дифференцируема
в точке
дифференцируема
в точке![]() , то частные производные в этой точке вычисляются по
формулам…
, то частные производные в этой точке вычисляются по
формулам…
№да
![]()
![]()
№нет
![]()
![]()
№нет
![]()
![]()
№нет
![]()
![]()
№Вопрос1
Полный
дифференциал функции двух переменных ![]() вычисляется по
формуле…
вычисляется по
формуле…
№да
![]()
№нет
![]()
№нет
![]()
№нет
![]()
№Вопрос1
Дифференциал
второго порядка для функции двух переменных ![]() в случае
непрерывности смешанных производных вычисляется по формуле
в случае
непрерывности смешанных производных вычисляется по формуле
№да
![]()
№нет
![]()
№нет
![]()
№нет
![]()
№Вопрос1
Функция
![]() называется
называется ![]() -раз
дифференцируемой в точке
-раз
дифференцируемой в точке ![]() , если…
, если…
№да
в некоторой
окрестности этой точки существуют все частные производные (n-1)-го порядка от этой функции, причем, все они
являются дифференцируемыми функциями относительно ![]() и
и ![]() в точке
в точке ![]()
№нет
все
частные производные n-го порядка от этой функции
являются дифференцируемыми функциями относительно ![]() и
и ![]() в окрестности точки
в окрестности точки ![]()
№нет
все
частные производные (n-1)-го порядка от
этой функции являются дифференцируемыми функциями относительно ![]() и
и ![]() в окрестности точки
в окрестности точки ![]()
№нет
в
некоторой окрестности этой точки существуют все частные производные n-го порядка от этой функции
№Вопрос1
Если
функция ![]() является n-раз
дифференцируемой в некоторой окрестности точки
является n-раз
дифференцируемой в некоторой окрестности точки ![]() , то…
, то…
№да
в
каждой точке ![]() из этой
окрестности выполняется следующее равенство:
из этой
окрестности выполняется следующее равенство:
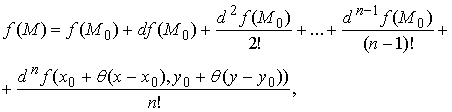
где
![]()
№нет
существует
хотя бы одна точка ![]() из этой
окрестности, для которой выполняется следующее равенство:
из этой
окрестности, для которой выполняется следующее равенство:
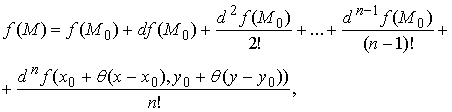
где
![]()
№нет
существует
только одна точка ![]() из этой
окрестности, для которой выполняется следующее равенство:
из этой
окрестности, для которой выполняется следующее равенство:
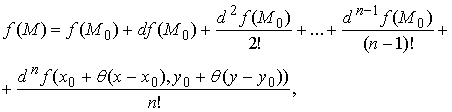
где
![]()
№нет
существуют
только две точки ![]() и
и ![]() из этой
окрестности, для которой выполняется следующее равенство:
из этой
окрестности, для которой выполняется следующее равенство:
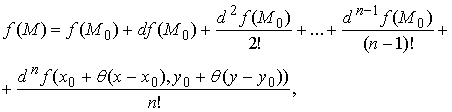
где
![]()
№Вопрос1
Уравнение
![]() определяет
неявную функцию
определяет
неявную функцию ![]() многих
переменных на параллелепипеде
многих
переменных на параллелепипеде ![]() , если…
, если…
№да
![]()
![]() уравнение
уравнение ![]() имеет
единственное решение
имеет
единственное решение ![]()
№нет
![]()
![]() , для которой уравнение
, для которой уравнение ![]() имеет
единственное решение
имеет
единственное решение ![]()
№нет
![]()
![]() уравнение
уравнение ![]() имеет хотя бы
одно решение
имеет хотя бы
одно решение ![]()
№нет
![]()
![]() , для которой уравнение
, для которой уравнение ![]() имеет хотя бы
одно решение
имеет хотя бы
одно решение ![]()
№Вопрос1
Точка
![]() называется
точкой локального максимума функции
называется
точкой локального максимума функции ![]() , определенной в некоторой окрестности данной точки,
если…
, определенной в некоторой окрестности данной точки,
если…
№да
существует
сферическая окрестность точки ![]() такая, что для
любой точки
такая, что для
любой точки![]() из этой окрестности выполняется неравенство
из этой окрестности выполняется неравенство ![]()
№нет
существует
сферическая окрестность точки ![]() такая, что для
любой точки
такая, что для
любой точки![]() из этой окрестности выполняется неравенство
из этой окрестности выполняется неравенство ![]()
№нет
для
любой сферической окрестности точки ![]() существует точка
существует точка
![]() из этой
окрестности, для которой выполняется неравенство
из этой
окрестности, для которой выполняется неравенство ![]()
№нет
для
любой сферической окрестности точки ![]() существует точка
существует точка
![]() из этой
окрестности, для которой выполняется неравенство
из этой
окрестности, для которой выполняется неравенство ![]()
№Вопрос1
Точка
![]() называется
точкой локального минимума функции
называется
точкой локального минимума функции ![]() , определенной в некоторой окрестности данной точки,
если…
, определенной в некоторой окрестности данной точки,
если…
№да
существует
сферическая окрестность точки ![]() такая, что для
любой точки
такая, что для
любой точки![]() из этой окрестности выполняется неравенство
из этой окрестности выполняется неравенство ![]()
№нет
существует
сферическая окрестность точки ![]() такая, что для
любой точки
такая, что для
любой точки![]() из этой окрестности выполняется неравенство
из этой окрестности выполняется неравенство ![]()
№нет
для
любой сферической окрестности точки ![]() существует точка
существует точка
![]() из этой
окрестности, для которой выполняется неравенство
из этой
окрестности, для которой выполняется неравенство ![]()
№нет
для
любой сферической окрестности точки ![]() существует точка
существует точка
![]() из этой
окрестности, для которой выполняется неравенство
из этой
окрестности, для которой выполняется неравенство ![]()
№Вопрос1
Если
функция ![]() имеет локальный
экстремум в точке
имеет локальный
экстремум в точке ![]() и в этой точке
существует конечная частная производная
и в этой точке
существует конечная частная производная  по данному
аргументу
по данному
аргументу ![]()
![]() , то…
, то…
№да
она
обращается в нуль
№нет
она
больше нуля
№нет
она
меньше нуля
№нет
она
в некоторых точках положительна, а в
некоторых- отрицательна
№Вопрос1
Если
функция ![]() имеет локальный
экстремум в точке
имеет локальный
экстремум в точке ![]() , сама функция дифференцируема в этой точке, то…
, сама функция дифференцируема в этой точке, то…
№да
ее
дифференциал равен нулю
№нет
ее
дифференциал положительный
№нет
ее
дифференциал отрицательный
№нет
ее
дифференциал в некоторых точках положительный, а в некоторых-
отрицательный
№Вопрос1
Для
того чтобы симметричная квадратичная форма  была
положительно определенной необходимо и достаточно, чтобы…
была
положительно определенной необходимо и достаточно, чтобы…
№да
все
главные миноры матрицы этой квадратичной формы были положительными
№нет
хотя
бы два главных минора матрицы этой квадратичной формы были положительными
№нет
хотя
бы один главный минор матрицы этой квадратичной формы был положительным
№нет
главные
миноры матрицы этой формы чередовали свой знак, начиная с плюса
№Вопрос1
Для
того чтобы симметричная квадратичная форма  была
отрицательно определенной необходимо и достаточно, чтобы…
была
отрицательно определенной необходимо и достаточно, чтобы…
№да
главные
миноры матрицы этой формы чередовали свой знак, начиная с минуса
№нет
все
главные миноры матрицы этой квадратичной формы были отрицательными
№нет
хотя
бы один главный минор матрицы этой квадратичной формы был отрицательным
№нет
хотя
бы два главных минора матрицы этой квадратичной формы были отрицательными
№Вопрос1
Если
функция ![]() дважды
дифференцируема в некоторой точке
дважды
дифференцируема в некоторой точке ![]() ,
, ![]() , частные производные второго порядка
, частные производные второго порядка  непрерывны в
точке
непрерывны в
точке ![]() , то…
, то…
№да
![]() - точка
локального минимума функции
- точка
локального минимума функции ![]() , если
, если ![]() является
положительно определенной квадратичной формой относительно дифференциалов
аргументов
является
положительно определенной квадратичной формой относительно дифференциалов
аргументов
№нет
![]() - точка
локального минимума функции
- точка
локального минимума функции ![]() , если
, если ![]() является отрицательно
определенной квадратичной формой относительно дифференциалов аргументов
является отрицательно
определенной квадратичной формой относительно дифференциалов аргументов
№нет
![]() - точка
локального минимума функции
- точка
локального минимума функции ![]() , если
, если ![]() является знаконеопределенной квадратичной формой относительно
дифференциалов аргументов
является знаконеопределенной квадратичной формой относительно
дифференциалов аргументов
№нет
![]() - точка
локального минимума функции
- точка
локального минимума функции ![]() , если
, если ![]() является
полуопределенной квадратичной формой относительно дифференциалов аргументов
является
полуопределенной квадратичной формой относительно дифференциалов аргументов
№Вопрос1
Если
функция ![]() дважды
дифференцируема в некоторой точке
дважды
дифференцируема в некоторой точке ![]() ,
, ![]() , частные производные второго порядка
, частные производные второго порядка  непрерывны в
точке
непрерывны в
точке ![]() , то…
, то…
№да
![]() - точка локального
максимума функции
- точка локального
максимума функции ![]() , если
, если ![]() является
отрицательно определенной квадратичной формой относительно дифференциалов
аргументов
является
отрицательно определенной квадратичной формой относительно дифференциалов
аргументов
№нет
![]() - точка
локального максимума функции
- точка
локального максимума функции ![]() , если
, если ![]() является
положительно определенной квадратичной формой относительно дифференциалов
аргументов
является
положительно определенной квадратичной формой относительно дифференциалов
аргументов
№нет
![]() - точка
локального максимума функции
- точка
локального максимума функции ![]() , если
, если ![]() является знаконеопределенной квадратичной формой относительно
дифференциалов аргументов
является знаконеопределенной квадратичной формой относительно
дифференциалов аргументов
№нет
![]() - точка
локального максимума функции
- точка
локального максимума функции ![]() , если
, если ![]() является
полуопределенной квадратичной формой относительно дифференциалов аргументов
является
полуопределенной квадратичной формой относительно дифференциалов аргументов
№Вопрос1
Если
функция ![]() дважды
дифференцируема в некоторой точке
дважды
дифференцируема в некоторой точке ![]() ,
, ![]() , частные производные второго порядка
, частные производные второго порядка  непрерывны в
точке
непрерывны в
точке ![]() , то…
, то…
№да
![]() не является точкой локального экстремума
функции
не является точкой локального экстремума
функции ![]() , если
, если ![]() является
отрицательно определенной квадратичной формой относительно дифференциалов
аргументов
является
отрицательно определенной квадратичной формой относительно дифференциалов
аргументов
№нет
![]() не является
точкой локального экстремума функции
не является
точкой локального экстремума функции ![]() , если
, если ![]() является
положительно определенной квадратичной формой относительно дифференциалов
аргументов
является
положительно определенной квадратичной формой относительно дифференциалов
аргументов
№нет
![]() не является
точкой локального экстремума функции
не является
точкой локального экстремума функции ![]() , если
, если ![]() является знаконеопределенной квадратичной формой относительно
дифференциалов аргументов
является знаконеопределенной квадратичной формой относительно
дифференциалов аргументов
№нет
![]() не является
точкой локального экстремума функции
не является
точкой локального экстремума функции ![]() , если
, если ![]() является
полуопределенной квадратичной формой относительно дифференциалов аргументов
является
полуопределенной квадратичной формой относительно дифференциалов аргументов
№Вопрос1
Квадратичная
форма  , при
, при ![]() называется
положительно определенной, если…
называется
положительно определенной, если…
№да
![]()
![]() с
с ![]()
№нет
![]()
![]() с
с ![]()
№нет
![]() , для которых
, для которых ![]()
№нет
№Вопрос1
Квадратичная
форма  , при
, при ![]() называется
отрицательно определенной, если…
называется
отрицательно определенной, если…
№да
![]()
![]() с
с ![]()
№нет
![]()
![]() с
с ![]()
№нет
![]() , для которых
, для которых ![]()
№Вопрос1
Квадратичная
форма  , при
, при ![]() называется знаконеопределенной, если…
называется знаконеопределенной, если…
№да
существует
хотя бы одна пара точек ![]() и
и ![]() , для которых
, для которых ![]() и
и ![]()
№нет
существует
хотя бы одна пара точек ![]() и
и ![]() , для которых
, для которых ![]() и
и ![]()
№нет
существует
только одна точка ![]() , для которой
, для которой ![]()
№нет
существует
хотя бы одна пара точек ![]() и
и ![]() , для которых
, для которых ![]() и
и ![]()
№Вопрос1
В трехмерном пространстве
(или на плоскости) ![]() задано скалярное
поле, если каждой точке
задано скалярное
поле, если каждой точке ![]() поставлено в соответствие...
поставлено в соответствие...
№да
некоторое число ![]()
№нет
некоторый вектор ![]()
№нет
некоторая
матрица
№нет
некоторая
вектор-функция
№Вопрос2
В трехмерном пространстве
(или на плоскости) ![]() задано векторное
поле, если каждой точке
задано векторное
поле, если каждой точке ![]() поставлено в соответствие...
поставлено в соответствие...
№да
некоторый
вектор ![]()
№да
некоторая
вектор-функция
№нет
некоторое
число ![]()
№нет
некоторая
матрица
№Вопрос2
Примеры
скалярных полей ...
№да
поле
температур какого-либо тела
№да
поле
плотности зарядов на какой-либо поверхности или в сплошной среде
№нет
электрическое
поле системы электрических зарядов
№нет
магнитное
поле, создаваемое электрическим током
№Вопрос2
Примеры
скалярных полей ...
№да
поле
плотности зарядов на какой-либо поверхности или в сплошной среде №да
поле
плотности масс какого-либо тела
№нет
электрическое
поле системы электрических зарядов
№нет
магнитное
поле, создаваемое электрическим током
№Вопрос2
Примеры
векторных полей ...
№да
электрическое
поле системы электрических зарядов
№да
магнитное
поле, создаваемое электрическим током
№нет
поле
температур какого-либо тел
№нет
поле
плотности зарядов на какой-либо поверхности или в
сплошной сред
№Вопрос2
Примеры
векторных полей ...
№да
электрическое
поле системы электрических зарядов
№да
магнитное
поле, создаваемое электрическим током
№нет
поле
плотности зарядов на какой-либо поверхности или в сплошной среде №нет
поле
плотности масс какого-либо тела
№Вопрос1
Производная
по направлению  имеет вид...
имеет вид...
№да

№нет
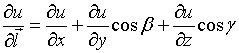
№нет
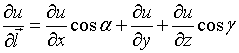
№нет
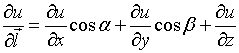
№Вопрос1
Производная
векторного поля ![]() по направлению
по направлению  имеет вид...
имеет вид...
№да
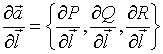
№нет
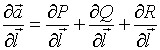
№нет
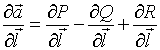
№нет
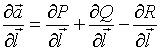
№Вопрос2
Градиентом
скалярного поля ![]() называется
вектор-функция...
называется
вектор-функция...
№да

№да
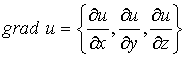
№нет
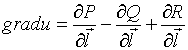
№нет
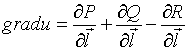
№Вопрос1
Дивергенцией векторного поля ![]() =
=![]() называется
скалярная функция...
называется
скалярная функция...
№да
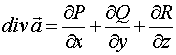
№нет
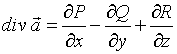
№нет
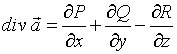
№нет
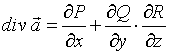
№Вопрос1
Ротором
(вихрем) векторного поля ![]() =
=![]() называется
вектор-функция....
называется
вектор-функция....
№да
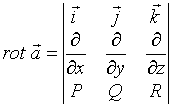
№нет
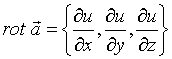
№нет
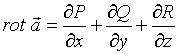
№нет