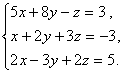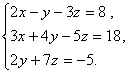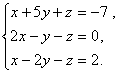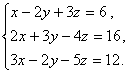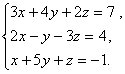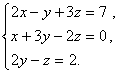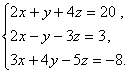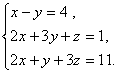МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное бюджетное образовательное учреждение

высшего образования

«ДАГЕСТАНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ»

Факультет математики и компьютерных наук

 

 

 

 

 

РАБОЧАЯ ПРОГРАММА ДИСЦИПЛИНЫ

 

Математика

 

 

                                                                                                                                                      Кафедра  математического анализа

                                                                                                                                             факультета математики и компьютерных наук

 

 

Образовательная программа

05.03.06  Экология и природопользование 

 

Профиль подготовки

Экология

 

 

                                                                                                                          Уровень высшего образования

бакалавриат

 

Форма обучения

очная

 

                                                                                                                             Статус дисциплины: базовая

 

 

 

 

 

 

 

                                                                                                                              Махачкала - 2017

 

Аннотация рабочей программы дисциплины

 

Дисциплина "Математика"  входит в базовую часть образовательной программы бакалавриата по направлению 05.03.06  Экология и природопользование.

Дисциплина реализуется  в институте экологии  и устойчивого развития кафедрой математического анализа факультета математики и компьютерных наук.

Содержание дисциплины охватывает круг вопросов, связанных:  с изучением и освоением  базовых понятий алгебры, геометрии,  математического анализа, элементов теории вероятностей и математической статистики, в частности, понятий: матрица, определитель, предел функции, ее непрерывность, дифференцирование и интегрирование;   понятий, связанных с решением систем линейных уравнений; с изучением метода координат и кривых второго порядка и поверхностей;  с изучением  свойств числовых и степенных рядов; с некоторыми методами решения дифференциальных уравнений.

 

Дисциплина нацелена на формирование общепрофессиональных компетенций выпускника  –  ОПК – 1.

 

Преподавание дисциплины предусматривает проведение следующих видов учебных занятий: лекции, практические занятия,  самостоятельная работа.

Рабочая программа дисциплины предусматривает проведение контроля успеваемости в форме контрольной работы и коллоквиума и промежуточного контроля в форме  зачета и экзамена.

 

Объем дисциплины  5  зачетных единиц, в том числе в академических часах по видам учебных занятий:

 

Семестр

Учебные занятия

Форма промежуточной аттестации

Всего

в том числе

Контактная работа обучающихся с преподавателем

СРС, в том числе экзамен

из них

Лекции

Лабораторные занятия

Практические занятия

КСР

консультации

1

72

16

 

16

 

 

40

 зачет

2

108

22

 

22

 

 

28+36

экзамен

Итого

180

38

 

38

 

 

68+36

 

 

1. Цели  освоения дисциплины

Целями освоения дисциплины  Математика  являются:

-- овладение основными методами решения систем линейных алгебраических уравнений;

-- овладение  основными  понятиями анализа (функция, предел  функции,   непрерывность  и  дифференцируемость  функции,  производные  и  дифференциалы  функции,  интеграл, ряд);

-- творческое  овладение   основными  методами  и технологиями  доказательства теорем  и решения  задач  математики;

-- овладение  методами дифференциального и интегрального исчисления,  методами решения дифференциальных уравнений;

-- методами математической статистики.

 

 2. Место дисциплины  в структуре ООП бакалавриата

Дисциплина Математика входит в базовую часть образовательной программы направления  05.03.06 Экология и природопользование.

 Знания  по математике студентам  необходимы  для изучения различных разделов экологии и биологии, а также для выполнения научно-исследовательской работы.

       Изучение  курса  высшей математики предполагает   хорошее   знание   школьного  курса  математики,  особенно  владение  тождественными  преобразованиями  алгебраических и  тригонометрических   выражений  и   знание   свойств  основных   элементарных  функций.

      

 3. Компетенции обучающегося, формируемые в результате освоения дисциплины

 

Компетенции

Формулировка компетенции из ФГОС ВО

Планируемые результаты обучения (показатели достижения заданного уровня освоения компетенций)

ОПК-1

Владение базовыми знаниями в области фундаментальных разделов математики в объеме, необходимом для владения математическим аппаратом экологических наук, обработки информации и анализа данных по экологии и природопользованию.

Знать: базовый материал  по линейной алгебре, аналитической геометрии и математическому анализу; элементы теории вероятностей и математической статистики.

Уметь:  давать  естественнонаучные интерпретации  и различные приложения теорем математического анализа и линейной алгебры; применять  математическую статистику в приложениях математики в экологических науках.

Владеть  методами теории рядов, интегралов,  дифференциальных уравнений и методами линейной алгебры, а также  элементами математической статистики для применения  в различных областях экологии.

 

 

4.Объем, структура и содержание дисциплины

4.1. Объем дисциплины составляет 5 зачетных единиц, 180  академических часов.

4.2. Структура дисциплины

 

 

 

Названия разделов и тем дисциплины

Семестр

Неделя семестра

Аудиторные занятия, в том числе

Самостоят. работа

 

Формы текущего контроля успеваемости (по неделям семестра)

Форма промежуточной аттестации (по семестрам)

лекции

практ. занятия

лабор. работы

Контр. сам. раб.

Первый семестр

Модуль 1. Элементы линейной алгебры

Всего по модулю 1

1

 

8

8

 

 

20

коллоквиум, контрольная работа

1.Действительные числа и действия над ними.

 

 

2

2

 

 

4

 

2.Матрицы и определители.

 

 

2

2

 

 

6

 

3. Системы линейных алгебраических уравнений.

 

 

4

4

 

 

10

 

Модуль 2.  Аналитическая геометрия

Всего по модулю 2

1

 

8

8

 

 

20

коллоквиум, контрольная работа

 

1.Метод  координат на плоскости и в пространстве. Уравнения прямой.

 

 

2

2

 

 

4

 

2.Кривые и поверхности второго порядка.

 

 

2

2

 

 

6

 

3.Графики уравнений. Преобразования графиков элементарных функций.

 

 

4

4

 

 

10

 

ИТОГО за первый семестр

 

 

16

16

 

 

40

зачет

Второй семестр

Модуль 1.  Дифференциальное  и интегральное исчисления

Всего по модулю 1

2

 

12

10

 

 

14

коллоквиум, контрольная работа

 

1. Предел числовой последовательности.

 

 

2

2

 

 

2

 

2. Предел и непрерывность функции.

 

 

2

2

 

 

2

 

3. Производные функций и их приложения.

 

 

2

2

 

 

3

 

4. Первообразная и неопределенный интеграл. 

 

 

4

2

 

 

4

 

5. Определенный интеграл. 

 

 

2

2

 

 

3

 

 

 

 

 

 

 

 

 

 

Модуль  2. Ряды. Элементы теории вероятностей и математической статистики

Всего по модулю 2

2

 

10

12

 

 

14

 

коллоквиум, контрольная работа

1. Числовые ряды. 

 

 

4

6

 

 

6

 

2. Функциональные ряды.

 

 

2

2

 

 

3

 

3.  Вероятность и условная вероятность. Схема Бернулли.

 

 

   2

   2

 

 

3

 

4. Случайные величины. Функция и плотность распределения.

 

 

   2

   2

 

 

2

 

 

 

 

 

 

 

 

 

 

Модуль 3.

Экзамен

 

 

 

 

 

 

 

36

ИТОГО за второй семестр

 

 

22

22

 

 

28

36

ВСЕГО                                                      38        38                                    68                      36

 

4.3. Содержание дисциплины, структурированное по темам (разделам)

ЛЕКЦИИ

Первый семестр

 

Модуль 1. Элементы линейной алгебры

Тема 1.Действительные числа и действия над ними.

Натуральные, целые, рациональные и иррациональные числа. Арифметические операции над ними. Числовая ось. Измерение отрезков.

Тема 2.Матрицы и определители.

Матрицы и действия над ними. Определители второго и третьего порядков и их

 

свойства. Ранг матрицы. Обратная матрица.

Тема 3. Системы линейных алгебраических уравнений.

Системы линейных алгебраических уравнений. Различные методы решения: метод Крамера, матричный метод, метод исключений Гаусса.

 

Модуль 2. Аналитическая геометрия

Тема 4. Метод координат на плоскости и в пространстве. Уравнения прямой. Прямоугольные координаты на плоскости и в пространстве. Общее уравнение прямой на плоскости. Уравнение прямой, проходящей через две данные точки. Уравнение прямой в отрезках. Уравнение прямой с угловым коэффициентом.

Уравнение плоскости. Уравнение прямой в пространстве.  Угол между прямыми в пространстве.

Тема 5. Кривые и поверхности второго порядка.

Окружность  и эллипс. Гипербола. Парабола. Сфера и эллипсоид. Гиперболоид. Параболоид.

Тема 6. Графики уравнений. Преобразования графиков элементарных функций.

Графическое изображение кривых, задаваемых уравнением. Сложение, умножение и другие преобразования графиков элементарных функций.

 

Второй  семестр

Модуль 1. Дифференциальное и интегральное исчисления

Тема 7. Предел числовой последовательности.

Последовательности действительных чисел. Предел  числовой   последовательности.  Свойства  сходящихся   последовательностей.   Переход  к  пределу   в неравенствах и  арифметических  операциях. Монотонные  последовательности.

Тема 8. Предел и непрерывность функции.

 Определение  предела  функции. Основная теорема о пределах.  Замечательные  пределы. 

Непрерывность.  Точки  разрыва. Свойства  непрерывных функций.

Тема 9. Производные функций и их приложения.

Определение   производной. Дифференцируемость   и   дифференциал   функции. Таблица   производных.  Правила  дифференцирования. Теоремы о среднем  дифференциального исчисления. Производные и  дифференциалы  высших  порядков. Формула   Тейлора. Исследование функций и построение графиков.

Частные   производные и дифференциалы. Задачи на экстремум  функций многих переменных.

Тема 10. Первообразная  и неопределенный интеграл.

Первообразная функция. Определение  неопределенного  интеграла.  Табличные  интегралы.  Метод замены   переменной.  Интегрирования  по   частям.

Тема 11. Определенный интеграл.

Определенный интеграл Римана и задачи, приводящие к нему. Основные свойства. Формула Ньютона-Лейбница. Интегрирование по частям и замена переменной.

 

Модуль 2.  Ряды. Элементы теории вероятностей и математической статистики

Тема 12. Числовые ряды.

Сходимость. Признаки сходимости рядов с положительными членами. Абсолютная и условная сходимость. Знакочередующиеся ряды.

Тема 13. Функциональные ряды.

Степенные ряды. Радиус и интервал сходимости. Свойства суммы. Разложение элементарных функций в ряд Тейлора. Приложения.  

Тема 14. Вероятность и условная вероятность события. Схема Бернулли.

Виды случайных событий. Операции над случайными событиями. Классическое определение вероятности. Свойства вероятности. Условная вероятность. Теоремы умножения и сложения вероятностей.  Независимые испытания. Формула Бернулли.

Тема 15. Случайные величины. Функция и плотность распределения.

Дискретные и непрерывные случайные величины. Функции распределения. Плотность распределения. Математическое ожидание и дисперсия, их свойства.  Примеры биномиальных, равномерных, показательных, пуассоновских, нормальных распределений.

    Модуль 3.  Подготовка к экзамену

 

ПРАКТИЧЕСКИЕ ЗАНЯТИЯ

Первый семестр

 

Модуль 1. Элементы линейной алгебры

Тема 1.Действительные числа и действия над ними.

Арифметические операции над действительными числами. Числовая ось. Измерение отрезков.

Тема 2.Матрицы и определители.

Матрицы и действия над ними. Определители второго и третьего порядков и их свойства. Ранг матрицы. Обратная матрица.

Тема 3. Системы линейных алгебраических уравнений.

Системы линейных алгебраических уравнений. Различные методы решения: метод Крамера, матричный метод, метод исключений Гаусса.

 

Модуль 2. Аналитическая геометрия

Тема 4. Метод координат на плоскости и в пространстве. Уравнения прямой. Прямоугольные координаты на плоскости и в пространстве. Общее уравнение прямой на плоскости. Уравнение прямой, проходящей через две данные точки. Уравнение прямой в отрезках. Уравнение прямой с угловым коэффициентом.

Уравнение плоскости. Уравнение прямой в пространстве.  Угол между прямыми в пространстве.

Тема 5. Кривые и поверхности второго порядка.

Окружность  и эллипс. Гипербола. Парабола. Сфера и эллипсоид. Гиперболоид. Параболоид.

Тема 6. Графики уравнений. Преобразования графиков элементарных функций.

Графическое изображение кривых, задаваемых уравнением. Сложение, умножение и другие преобразования графиков элементарных функций.

 

Второй  семестр

Модуль 1. Дифференциальное и интегральное исчисления

Тема 7. Предел числовой последовательности.

Последовательности действительных чисел. Предел  числовой   последовательности.  Свойства  сходящихся   последовательностей.   Переход  к  пределу   в неравенствах и  арифметических  операциях. Монотонные  последовательности.

Тема 8. Предел и непрерывность функции.

 Определение  предела  функции. Основная теорема о пределах.  Замечательные  пределы. 

Непрерывность.  Точки  разрыва. Свойства  непрерывных функций.

Тема 9. Производные функций и их приложения.

Вычисление  производных. Дифференцируемость   и   дифференциал   функции. Таблица   производных.  Правила  дифференцирования. Теоремы о среднем  дифференциального исчисления. Производные и  дифференциалы  высших  порядков. Формула   Тейлора. Исследование функций и построение графиков.

Частные   производные и дифференциалы. Задачи на экстремум  функций многих переменных.

Тема 10. Первообразная  и неопределенный интеграл.

Первообразная функция. Определение  неопределенного  интеграла.  Табличные  интегралы.  Метод замены   переменной.  Интегрирование  по   частям.

Тема 11. Определенный интеграл.

Основные свойства определенного интеграла. Формула Ньютона-Лейбница. Интегрирование по частям и замена переменной.

 

Модуль 2.  Ряды. Элементы теории вероятностей и математической статистики

Тема 12. Числовые ряды.

Сходимость. Признаки сходимости рядов с положительными членами. Абсолютная и условная сходимость. Знакочередующиеся ряды.

Тема 13. Функциональные ряды.

Степенные ряды. Радиус и интервал сходимости. Свойства суммы. Разложение элементарных функций в ряд Тейлора. Приложения.  

Тема 14. Вероятность и условная вероятность события. Схема Бернулли.

Виды случайных событий. Операции над случайными событиями. Классическое определение вероятности. Свойства вероятности. Условная вероятность. Теоремы умножения и сложения вероятностей.  Независимые испытания. Формула Бернулли.

Тема 15. Случайные величины. Функция и плотность распределения.

Дискретные и непрерывные случайные величины. Функции распределения. Плотность распределения. Математическое ожидание и дисперсия, их свойства.  Примеры биномиальных, равномерных, показательных, пуассоновских, нормальных распределений.

 

5. Образовательные технологии

В основе преподавания дисциплины математический анализ лежит лекционно-семинарская система обучения, что связано с необходимостью активного продумывания теоретического материала, содержащего глубокие и абстрактные понятия. Индивидуальные особенности обучающихся учитываются подбором заданий разного уровня сложности для самостоятельной работы студентов.

 По данной дисциплине учебным планом предусмотрено также проведение занятий в интерактивных формах.  Лекции проводятся в аудиториях, оснащенных видеопроекторами.  В университете функционирует Центр современных образовательных технологий, в котором предусматриваются мастер-классы специалистов.

 

6. Учебно-методическое обеспечение самостоятельной работы студентов.

 

Учебно-методические  пособия для самостоятельной работы

 

1.     Гайдаров  Д.Р. Математический  анализ. Ч.1 (Методическое  пособие  для  студентов I курса). Махачкала: ИПЦ ДГУ, 2002.

2.     Гайдаров  Д.Р. Математический  анализ. Ч. 2 (Методическое  пособие  для  студентов I курса). Махачкала: ИПЦ ДГУ, 2003.

3.     Гайдаров  Д.Р. Справочное  пособие  по математике. Махачкала , 2006.

 

Задания для самостоятельной работы

 

СР-1

 

 

1.      Вычислить определители:   ,  ,  .

2.     Найти произведение матриц: .

3.     Решить систему методом Крамера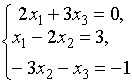

4.     Решить систему матричным методом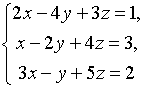

5.     Решить систему методом Гаусса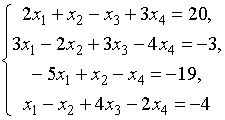

 

СР-2

 

1. Построить графики функций  а) ,  б) .

2. Найти пределы функций, не пользуясь правилом Лопиталя:

 1)        ; а) = 2; б) = -1; в) .

2)         .                  3)         .

3. Найти предел последовательности .

4. Найти пределы функций, используя правило Лопиталя:

  а) , б) .

5. Найти , если а) ;     б)       ;  в)     ;

 

 

СР-3

 

1. Найти  неопределенные  интегралы  .

2. Вычислить интегралы  .

3. Вычислить  площадь, ограниченную  графиками  функций    и   .

 

СР-4

 

1. Исследовать на сходимость числовые ряды:

1) ,   2)  ,  3) ,  4) , 5) , 6) .

 

2. Исследовать на абсолютную и условную сходимость ряды:

1)    ,    2)   ,  3) .

3. Найти области сходимости рядов:

1)    2) .

 

СР-5

 

1. Исследовать данные ряды на сходимость:

;   ;

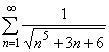
2. Найти область сходимости ряда:

 

 

 

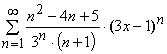
Разделы (модули)    и   темы  для самостоятельного изучения

 

Виды и содержание самостоятельной работы

Первый семестр

Модуль 1. Элементы линейной алгебры

 

1. Действительные числа и действия над ними.

Доклад на тему: Необходимость расширения множества рациональных чисел.

 

2.Матрицы и определители.

Решение задач и упражнений

 

2. Системы линейных алгебраических уравнений.

Решение задач и упражнений

 

Модуль 2. Аналитическая геометрия

 

1.  Метод координат на плоскости и в пространстве. Уравнения прямой.

Решение задач и упражнений

 

2. Кривые  и поверхности второго порядка.

Решение задач и упражнений

 

3. Графики уравнений. Преобразования графиков элементарных функций..

Решение задач и упражнений

 

Второй семестр

 

Модуль 1.  Дифференциальное  и интегральное исчисления

 

1. Предел числовой последовательности.

Доклады на темы:

1.  Монотонные последовательности.

2.Теорема Эйлера о числе е.

 

2. Предел и непрерывность функции.

Доклады на темы:

 1. Различные определения непрерывности.

 2. Обратные тригонометрические функции.

Решение задач и упражнений.

 

3.Производные функций и их приложения.

Доклад на тему:

1. Приложения производных высших порядков к исследованию функций.

 

 

4. Первообразная и неопределенный интеграл.

Решение задач и упражнений.

Реферат на тему:  Разложение рациональной функции на простейшие дроби.

 

5. Определенный интеграл.

Решение задач и упражнений.

Доклад на тему: Восстановление функции по ее производной.

6. Дифференциальные уравнения, интегрируемые в квадратурах.

Решение задач и упражнений

Модуль 2. Ряды. Элементы теории вероятностей и математической статистики

 

1. Числовые ряды.

Решение задач.

Доклады на темы:

1. Сравнение различных признаков сходимости числовых рядов.

2. Признак Лейбница сходимости знакочередующихся рядов.

3.  Синус- и косинус-ряды.

 

2. Функциональные ряды.

Решение задач и упражнений

 

3.Вероятность и условная вероятность.    Схема Бернулли.

Решение задач и упражнений.

 

4. Случайные величины. Функция и плотность распределения.

Решение задач и упражнений.

 

5. Статистические оценки.

Решение задач и упражнений.

 

 

 

7.  Фонд оценочных средств  для проведения текущего контроля успеваемости, промежуточной аттестации по итогам освоения дисциплины

 

7.1. Перечень компетенций с указанием этапов их формирования в процессе освоения образовательной программы.

Перечень компетенций с указанием этапов их формирования приведен в описании образовательной программы.

 

Компетенция

Знания, умения, навыки

Процедура освоения

ОПК-1

Знать: базовый материал  по линейной алгебре, аналитической геометрии и математическому анализу; элементы теории вероятностей и математической статистики.

Уметь:  давать  естественнонаучные интерпретации  и различные приложения теорем математического анализа и линейной алгебры; применять  математическую статистику в приложениях математики в экологических науках.

Владеть  методами теории рядов, интегралов,  дифференциальных уравнений и методами линейной алгебры, а также  элементами математической статистики для применения  в различных областях экологии.

Коллоквиум, контрольная работа,  экзамен

 

 

7.2. Описание показателей и критериев оценивания компетенций, описание шкал оценивания.

 

ОПК-1

Схема оценки уровня формирования компетенции «Владение базовыми знаниями в области фундаментальных разделов математики в объеме, необходимом для владения математическим аппаратом экологических наук, обработки информации и анализа данных по экологии и природопользованию»

 

 

Уровень

Показатели

(что обучающийся должен продемонстрировать)

Оценочная шкала

Удовлетворительно

Хорошо

Отлично

Пороговый

Знать: базовый материал  по линейной алгебре, аналитической геометрии и математическому анализу; элементы теории вероятностей и математической статистики.

Уметь:  давать  естественнонаучные интерпретации  и различные приложения теорем математического анализа и линейной алгебры; применять  математическую статистику в приложениях математики в экологических науках.

Владеть  методами теории рядов, интегралов,  дифференциальных уравнений и методами линейной алгебры, а также  элементами математической статистики для применения  в различных областях экологии.

Допускает ошибки

при формулировке основных определений  по материал  по линейной алгебре, аналитической геометрии и математическому анализу, знает элементы теории вероятностей и математической статистики.

Умеет  давать некоторые  приложения теорем математического анализа и линейной алгебры в экологических науках.

Владеет в некоторой степени методами теории рядов, интегралов,  дифференциальных уравнений и методами линейной алгебры, а также методами статистики.

Допускает неточности при формулировке основных определений  по материал  по линейной алгебре, аналитической геометрии и математическому анализу, не в полной мере знает  элементы теории вероятностей и математической статистики.

Умеет  давать различные приложения теорем математического анализа и линейной алгебры; применять  математическую статистику в приложениях математики в экологических науках.

Владеет в достаточной степени  методами теории рядов, интегралов,  дифференциальных уравнений и методами линейной алгебры, а также  элементами математической статистики для применения  в различных областях экологии.

Знает базовый материал  по линейной алгебре, аналитической геометрии и математическому анализу; элементы теории вероятностей и математической статистики.

Умеет  давать различные приложения теорем математического анализа и линейной алгебры; применять  математическую статистику в приложениях математики в экологических науках.

Владеет  методами теории рядов, интегралов,  дифференциальных уравнений и методами линейной алгебры, а также  элементами математической статистики для применения  в различных областях экологии.

 

Если хотя бы одна из компетенций не сформирована, то положительной оценки по дисциплине быть не может.

 

7.3. Типовые контрольные задания

 

Примерные  контрольные  вопросы  к  коллоквиуму по  разделу «Элементы линейной алгебры»

 

1.     Матрицы и действия над ними.

2.     Ранг матрицы.

3.     Определители второго и третьего порядков и их свойства.

4.     Системы линейных алгебраических уравнений.

5.     Метод Крамера решения систем.

6.     Метод Гаусса решения систем.

Примерные  контрольные  вопросы к коллоквиуму по  разделу «Аналитическая геометрия»

 

1. Уравнение прямой на плоскости и в пространстве.

2. Угол между прямыми.

3. Окружность и эллипс.

4. Гипербола.

5. Парабола.

 

Примерные  контрольные  вопросы к коллоквиуму  по  разделу   «Дифференциальное исчисление»

 

1. Предел числовой последовательности.

2. Свойства сходящихся последовательностей.

3. Предел функции.

4. Бесконечно малые и бесконечно большие функции.

5. Замечательные пределы.

6. Непрерывность функции.

7. Точки разрыва функции.

8. Свойства непрерывных функций.

9. Определение производной.

10. Дифференцируемость и дифференциал функции.

11. Таблица производных. Правила нахождения производных. Геометрический смысл производной.

12. Основные теоремы дифференциального исчисления.

13. Раскрытие неопределенностей. Правило Лопиталя.

14. Производные высших порядков.

15. Формула Тейлора.
16.Условия монотонности функции. Условия экстремума функции.

17. Условия выпуклости функции. Точки перегиба.

18. Асимптоты графика функции.

19. Общая схема исследования и построения графика функции.

20. Частные производные. Дифференцируемость.

21. Частные производные и дифференциалы высших порядков.

22. Исследование функций многих переменных на экстремум.

 

Примерные  контрольные  вопросы  коллоквиума по  разделу

 «Интегральное исчисление»

 

1. Первообразная.  Неопределенный интеграл. Таблица неопределенных интегралов.

2. Метод замены переменной.

3. Интегрирование по частям в неопределенном интеграле.

4. Интегралы от простейших дробей.

5. Задача вычисления площади криволинейной трапеции.

6. Определение определенного интеграла.

7. Свойства определенного интеграла.

8. Формула Ньютона-Лейбница.

9. Замена переменной в определенном интеграле.

10. Интегрирование по частям в определенном интеграле.

11. Геометрические приложения определенного интеграла.

 

Примерные  контрольные  вопросы  коллоквиума по  разделу

 «Ряды»

 

1. Сходимость и сумма числового ряда.

2. Необходимый признак сходимости числового ряда.

3. Признаки сравнения для знакоположительных рядов.

4. Достаточные условия сходимости знакоположительных рядов.

5. Абсолютная и условная сходимости. Признак Лейбница.

6. Функциональный ряд. Область сходимости функционального ряда.

7. Степенной ряд. Интервал и радиус сходимости.

 

Примерные  контрольные  вопросы  коллоквиума по  разделу

 «Элементы теории вероятностей и математической статистики»

 

1. Испытания и события. Виды случайных событий.

2. Классическое определение вероятности. Основные формулы комбинаторики. Примеры непосредственного вычисления вероятностей.

3.Теорема сложения вероятностей несовместных событий.

4. Произведение событий. Условная вероятность. Теорема умножения вероятностей. Независимые события. Теорема умножения для независимых событий.

5. Формула Бернулли.

6. Случайная величина. Дискретные и непрерывные случайные величины.

7.Числовые характеристики дискретных случайных величин. Математическое ожидание дискретной случайной величины. Свойства математического ожидания.

8. Дисперсия дискретной случайной величины. Формула для вычисления дисперсии. Свойства дисперсии.

9. Среднее квадратическое отклонение.

10. Определение функции распределения. Свойства функции распределения. График функции распределения.

11. Нормальное распределение. Нормальная кривая.  Вероятность попадания в заданный интервал нормальной случайной величины.

 

Примерные задания для проведения  текущего контроля

Дана система линейных уравнений: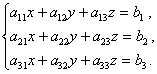

Доказать ее совместимость и решить тремя способами:

1) методом Гаусса;

2) средствами матричного исчисления;

3) правилом Крамера.

 


Найти пределы функций, не пользуясь правилом Лопиталя.

 

1)         ; а) = 2; б) = -1; в) .

2)         .                  3)         .

4)         ; а) = -1; б) = 1; в) .

5)         .              6)         .

7)         ; а) = 2; б) = -2; в) .

8)         .                 9)         .

10)       ; а) = 1; б) = 2; в) .

 

Исследовать методами дифференциального исчисления функцию  и построить ее график.

 

.

.

 

.

..

.

.

 

 

Найти неопределенные интегралы.

 

а);  б);    в);     г);  д).

 

В задачах: а) исследовать на сходимость с помощью признака Даламбера числовой ряд;

б) исследовать на сходимость с помощью признака Лейбница знакочередующийся ряд;

в) найти радиус сходимости степного ряда и определить тип сходимости ряда на концах интервала сходимости.

1.                     а) ;                     б) ;       в) ;

2.                     а) ;               б) ;      в) ;

3.                     а) ;          б) ;           в) .

Найти вероятности указанных событий, пользуясь правилами сложения и умножения вероятностей.

 

1.                  Для сигнализации об аварии установлены два независимо работающих сигнализатора. Вероятность того, что при аварии сработает первый сигнализатор, равна 0,95; второй сигнализатор срабатывает с вероятностью 0,8. Найти вероятность того, что при аварии сработает только один сигнализатор.

2.                  Отдел технического контроля проверяет изделия на стандартность. Вероятность того, что наугад взятое изделие окажется бракованным, равна 0,15. Проверено три изделия. Какова вероятность того, что два из них бракованные?

3.                  В группе студентов, состоящей из 20 человек, 12 юношей и 8 девушек. Для дежурства случайным образом отобрано двое студентов. Какова вероятность того, что среди них будет один юноша и одна девушка?

4.                  В ящике имеется 12 деталей, из которых 5 деталей нестандартны. Сборщик наудачу извлекает из ящика 4 детали. Какова вероятность того, что все они будут нестандартными?

5.                  Студент знает 15 из 20 вопросов программы. Какова вероятность того, что он знает все три вопроса, предложенные экзаменатором?

 

 

Дискретная величина Х может принимать только два значения:  и , причем . Известны вероятность  возможного значения , математическое ожидание  и дисперсия . Найти закон распределения этой случайной величины.

1.;; ;

2.;;;

3.;;.

 

7.4. Методические материалы, определяющие процедуру оценивания знаний, умений, навыков и (или) опыта деятельности, характеризующих этапы формирования компетенций.

Общий результат выводится как интегральная оценка, складывающая из текущего контроля - 50% и промежуточного контроля - 50%.

Текущий контроль по дисциплине включает:

- посещение занятий - 10 баллов,

- выполнение домашних контрольных работ – 10 баллов,

- участие на практических занятиях - 10 баллов,

- коллоквиум – 30 баллов,

- выполнение аудиторных контрольных работ - 40 баллов.

Промежуточный контроль по дисциплине включает:

- устный опрос (экзамен) - 100 баллов,

 

8. Перечень основной и дополнительной учебной литературы, необходимой для освоения дисциплины

 

а) основная литература:

 

1.     Гельфанд И.М. Лекции по линейной алгебре. М., 1999.

2.     Шевцов Г.С. Линейная алгебра.  М., 1999.

3.     Щипачев В.С. Высшая математика.- М.: Высшая школа, 1990.

4.     Кудрявцев Л.Д. Курс математического анализа. М.: Высшая школа, т.1,2, 1997.

5.     Бугров Я.С., Никольский С.М.  Высшая математика. Дифференциаль­ное и интегральное исчисление. М.: Наука, 1980.

6.     Берман Г.Н. Сборник задач по курсу математического анализа. М.: Высшая школа, 1997.

7.     Бугров Я.С., Никольский С.М. Высшая математика. Задачник. М.: Наука, 1987.

8.     Васильева А.Б., Тихонов А.Н., Свешников А.Г. Дифференциальные уравнения. М.: Изд. МГУ, 1989.

9.     Гмурман В. Е. Теория вероятно­стей и математи­ческая статистика. М.: Высш. школа, 2000.

10. Гмурман В. Е. Руководство к ре­шению задач по теории вероятно­стей и математической статистике. М.: Высшая школа, 2006

 

б) дополнительная литература:

 

1.     Беклемешев Д.В. Курс аналитической геометрии и линейной алгебры. М.: Наука, 1987.

2.     Клетеник Д.В. Сборник задач по аналитической геометрии. М.: Нау­ка, 1980.

3.     Ильин В. А. , Позняк Э. Г. Основы математического анализа. М.: Наука, т. 1, 2, 2002.

4.     Фихтенгольц Г. М. Основы математического анализа. М.: Нау­ка, т. 1, 2, 2016.

5.     Краснов М.Л. Обыкновенные дифференциальные уравнения.  М.: Высшая школа, 2010.

6.     Чистяков В.П. Курс теории вероятностей.  М.: Наука, 1988.

7.     Зубков А.М., Севастьянов Б.А., Чистяков В.П. Сборник задач по тео­рии  вероятностей. М.: Наука, 1989.

 

9. Перечень ресурсов информационно-телекоммуникационной сети «Интернет», необходимых для освоения дисциплины 

 

1. Федеральный портал http://edu.ru:

2. Электронные каталоги Научной библиотеки ДГУ http://elib.dgu.ru:

http://edu.icc.dgu.ru:

 

10. Методические указания для обучающихся по освоению дисциплины

 

Учебная программа по математике распределена по темам и по часам на лекции и практические занятия; предусмотрена также самостоятельная учебная работа студентов. По каждой теме преподаватель указывает студентам необходимую литературу (учебники, учебные пособия, сборники задач и упражнений), а также соответствующие темам параграфы и номера упражнений и задач.

Самостоятельная работа студентов складывается из работы над лекциями,  с учебниками, решения рекомендуемых  задач, подготовки к защите лабораторных работ, а также из подготовки к контрольным работам, коллоквиумам и сдаче зачетов и экзаменов.

При работе с лекциями и учебниками особое внимание следует уделить изучению основных понятий и определений по данному разделу, а также особенностям примененных методов и технологий доказательства теорем. Решение достаточного количества задач по данной теме поможет творческому овладению методами доказательства математических утверждений.

После изучения каждой темы рекомендуется самостоятельно воспроизвести основные определения, формулировки и доказательства теорем. Для самопроверки рекомендуется также использовать контрольные вопросы, приводимые в учебниках после каждой темы.

Основная цель практических занятий – подготовка студентов к самостоятельной работе над теоретическим материалом и к решению задач и упражнений.

 

11. Перечень информационных технологий, используемых при осуществлении образовательного процесса по дисциплине, включая перечень программного обеспечения и информационных справочных систем.

 

При осуществлении образовательного процесса по математике рекомендуются компьютерные технологии, основанные на операционных системах Windows, Ubuntu, Linux, прикладные программы Mathcad, Matlab, Mathematica, а также сайты образовательных учреждений и журналов, информационно-справочные системы, электронные учебники.

При проведении занятий рекомендуется использовать компьютеры, мультимедийные проекторы, интерактивные экраны.

 

12. Описание материально-технической базы, необходимой для осуществления образовательного процесса по дисциплине.

 

Университет обладает достаточной базой аудиторий для проведения всех видов занятий, предусмотренных образовательной программой дисциплины математический анализ. Кроме того, на факультете имеются компьютерные и  учебные классы, оснащенные компьютерами с соответствующим программным обеспечением и мультимедиа-проекторами.

В университете имеется необходимый комплект лицензионного программного обеспечения.